Published online Mar 16, 2021. doi: 10.12998/wjcc.v9.i8.1814
Peer-review started: September 24, 2020
First decision: December 14, 2020
Revised: January 6, 2021
Accepted: January 25, 2021
Article in press: January 25, 2021
Published online: March 16, 2021
Processing time: 162 Days and 1.9 Hours
With the modernization of society and transportation in the last decades in China, the incidence of high-energy trauma increased sharply in China, including that of acetabular fractures.
To establish different finite element models for acetabular posterior column fractures involving the quadrilateral area of the acetabulum.
The three-dimensional models of the normal and fractured pelvis and the five internal fixations were established using the computed tomography data of the pelvis of a living volunteer. After the vertebral body model was inserted in the way of origin matching and all cancellous bones were copied using the duplicated cancellous bone model as the subtractive entity, the Boolean operation was performed on the pelvis model to obtain the model of the complete pelvis cortical and cancellous bones.
In the standing position, the maximum stress was 46.21 MPa. In the sitting position, the sacrum bore the simulated gravity load at the upper end. When comparing the five fixations, there were no significant differences in the stress mean values among groups (sitting: P = 0.9794; standing: P = 0.9741). In terms of displacement, the average displacement of the internal iliac plate group was smaller than that of the spring plate group (P = 0.002), and no differences were observed between the other pairs of groups (all P > 0.05). In the standing position, there were no significant differences in the mean value of displacement among the groups (P = 0.2985). It can be seen from the stress nephogram of the internal fixations in different positions that the stress of the internal fixation was mainly concentrated in the fracture segment.
There were no significant differences among the fixations for acetabular posterior column fractures involving the quadrilateral area of the acetabulum.
Core Tip: Acetabular fractures are challenging, especially fractures of the quadrilateral area. Obtaining a three-dimensional finite element model of the pelvis is an effective method for biomechanical research and can provide some basis for the biomechanical characteristics of different fixation methods. This study aimed to establish different finite element models (in simulated standing and sitting positions) of the internal iliac plate, combined plate of anterior and posterior columns, triangle plate, row nail blocking, and spring plate for acetabular posterior column fractures involving the quadrilateral area of the acetabulum. The results suggest that there are no significant differences among the fixations.
- Citation: Xie XJ, Cao SL, Tong K, Zhong ZY, Wang G. Three-dimensional finite element analysis with different internal fixation methods through the anterior approach. World J Clin Cases 2021; 9(8): 1814-1826
- URL: https://www.wjgnet.com/2307-8960/full/v9/i8/1814.htm
- DOI: https://dx.doi.org/10.12998/wjcc.v9.i8.1814
With the modernization of society and transportation in the last several decades in China, the incidence of high-energy trauma, including acetabular fractures, has increased sharply in China[1-3]. The life-time prevalence of hip fracture is 20% in women and 10% in men[4], and acetabular fractures represent 18% of the total hip arthroplasty procedures in Chinese patients[5]. In China from 2002 to 2006, the incidence of hip fractures increased 2.8- and 1.6-fold in women and men, respectively[6]. The treatment of acetabular fracture is challenging. Presently, the primary treatment of displaced acetabular fracture is still open reduction and internal fixation[4,7-11].
The fractures of the quadrilateral area of the acetabulum are not included in the Letournel classification[12,13], but many complex fractures of the acetabular posterior column involve the quadrilateral area of the acetabulum[14,15]. Although the load-bearing area of the acetabulum is mainly at its top, not at the quadrilateral area, when a high-energy injury occurs, the quadrilateral area as a part of the inner wall of the posterior column is often hit into the pelvis by the femoral head and displaced together with the posterior column[15]. Moreover, anatomical reduction and fracture fixation aim to restore the matching relationship of the acetabulum and avoid leaving a central subluxation of the hip joint and traumatic arthritis, with a significant impact on clinical efficacy[11,16,17]. Previous studies suggested using a 1/3 tubular steel plate or L-shaped steel plate to block the displacement of the acetabulum-related structures[15,18,19]. Zha et al[16] suggested using a multidirectional fixation device with pelvic brim long screws. Nevertheless, the preoperative planning of such fractures is complicated because of the complex anatomy of the hip.
In the traditional biomechanical studies of the pelvis, human cadavers are often used, but the measurements of displacement and stress in cadaver specimens inevitably lead to large errors. Cadaveric specimens have the disadvantages of high cost, limited availability, and difficulty in repeated tests. In addition, cadaveric specimens will lead to systematic errors because even though the bones and joints retain their properties, the properties of the soft tissues will inevitably suffer from rigor mortis and the fixative/preservative solutions. In many studies, the soft tissues are removed, and only the bones and the joint are kept, but all information about the contribution of the tendons, fascia, and muscles to the stability of the joint is lost[20,21]. Therefore, at present, three-dimensional (3D) finite element modeling is an effective method for biomechanical research[22,23]. Nevertheless, in order to ensure the success of the experiment and the accuracy of the data, it is necessary to reconstruct the bone model accurately. The pelvis and acetabulum are a complex bony structure with cancellous bone sandwiched in the cortex[24]. Because the muscles and ligaments around the acetabulum play an indispensable role in stabilizing the pelvis bone structure and reducing stress concentration[25], it is necessary to pay attention to the addition of important ligaments when modeling to obtain a 3D finite element model of the pelvis with high simulation value and good stability.
At present, no biomechanical study has evaluated the stability of a 3D finite element model for the modeling of the treatment of acetabular posterior column fractures involving the quadrilateral area of the acetabulum. Therefore, the present study aimed to use a finite element model to establish different internal fixation models of the internal iliac plate, combined plate of anterior and posterior columns, triangle plate, row nail blocking, and spring plate and to simulate the standing and sitting positions. Using advanced mathematical modeling techniques, a mathematical model of an actual hip joint was obtained and could be used to measure forces, and stresses could be measured at specific points and under different conditions. The results will provide a basis for determining the biomechanical characteristics of the fixation of acetabular posterior column fractures.
A 48-year-old healthy male volunteer was selected as the research subject. This individual had undergone a vasectomy and had no plans for fertility. The risks and possible harms were carefully explained, and he signed the informed consent form, which was first approved by the ethics committee along with the study protocol. His pelvis was scanned using a dual-source 16-row computed tomography scanner (Siemens, Erlangen, Germany). The bone tissue window was selected for scanning. The thickness of the scanning layers was 1.0 mm, and the scanning range was from the upper edge of the fifth lumbar vertebra to the upper part of the bilateral femur, including the whole ischial tubercle. The computed tomography images were imported into Mimics 17.0 (Materialise, Leuven, Belgium) to generate the 3D model of the pelvis. The .stl file saved from Mimics 17.0 was opened in Geomagic Studio 2013 (Geomagic Inc., Morrisville, NC, United States), and the model was subdivided by 4 × mesh to ensure that no serious deformation occurred during model processing. The accurate pelvis, sacrum, and femur models were obtained after removing the redundant deformation features of the model and the sharp nail-like objects. The precise surface module was used to detect the contour of the model, edit the deformed or unreasonable contours, add the contour appropriately, and generate more regular surface pieces to fit the surface model. Then, the geometry model was exported to the general Step format to build a 3D model of a normal pelvis.
Using SolidWorks 2014 (Dassault Systems SolidWorks Corporation, Waltham, MA, United States) and according to the software prompts, feature recognition and surface diagnosis of the geometric models were carried out, and the problematic surfaces were repaired. Then, the model was saved to the SLDPRT part format. After the vertebral body model was inserted in the way of origin matching and all cancellous bones were copied using the duplicated cancellous bone model as the subtractive entity, the Boolean operation was performed on the pelvis model to obtain the model of the complete pelvis cortical and cancellous bones. The upper and lower surfaces of each sacrum and pelvis cortical bone were treated equidistantly, and the equidistant distance was 0 mm. The sacroiliac joint cartilage was established between them. The redundant part of the equidistant surface was then excised to make it fit the sacrum and pelvis entirely. Similarly, the acetabulum cartilage on both sides was generated, and a completely normal 3D model was obtained. The above geometric model was imported into Ansys 17.0 (ANSYS Inc., Canonsburg, PA, United States), and the analysis type was specified as “Static Structural.” Then, the property parameters of each material were set in the material library, as shown in Table 1.
| Part | Modulus of elasticity in MPa | Poisson’s ratio |
| Pubic cartilage | 5.00 | 0.45 |
| Interosseous sacroiliac ligament | 5610.00 | 0.20 |
| Sacrum | 6140.00 | 0.30 |
| Sacrospinous ligament | 12.60 | 0.20 |
| Sacrotuberous ligament | 46.48 | 0.300 |
| Sacroiliac joint cartilage | 54.00 | 0.40 |
| Iliac cancellous bone | 132.00 | 0.20 |
| Femur | 18200.00 | 0.38 |
| Posterior sacroiliac ligament | 133.00 | 0.20 |
| Acetabular cartilage | 12.00 | 0.42 |
| Iliac cortical bone | 17000.00 | 0.30 |
| Anterior sacroiliac ligament | 208.00 | 0.20 |
In the connection interface, the contact type between each structure was defined, in which the contact of the joint surface was set to “frictional,” and the corresponding friction coefficient was 0.5. The other contact types were set as “bonded,” which means that the relative position relationship of the structures on both sides of the contact surface was fixed. The spring element was used to simulate the ligament, and the tensile stiffness of each ligament was set. Next, the model was divided into meshes. In order to ensure the accuracy of the calculation to meet the requirements of the analysis, the type and size of the mesh were controlled. The mesh was set as the tetrahedral mesh with a size of 2 mm. Finally, the 3D finite element model of the pelvis was generated without error (Figure 1).
The right acetabular posterior column fracture model involving the quadrilateral area of the acetabulum was finally generated by setting up the reference plane, marking the fracture line, and cutting the fracture model according to the fracture line (Figure 2).
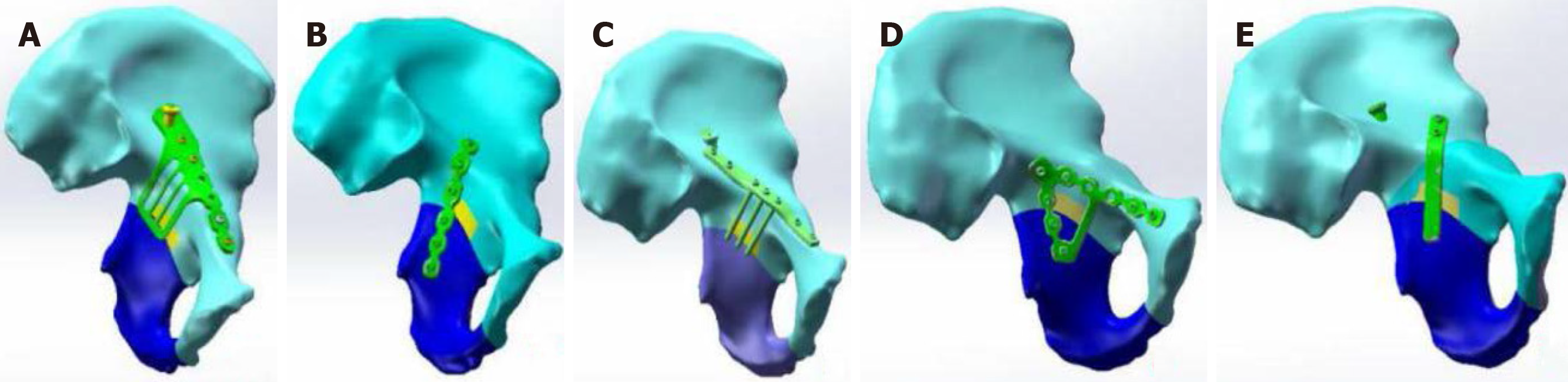
Using SolidWorks 2014 (Dassault Systems SolidWorks Corporation, Waltham, MA, United States), the models of the combined steel plate of anterior and posterior columns, internal iliac steel plate, row nail, triangle steel plate, and spring steel plate were generated by determining the equidistant surface, setting the datum plane and drawing the sketch of steel plate, drawing the boss, cutting with the tangent plane, cutting and stretching, and drawing the details of the steel plate. Then, they were imported into the 3D model of the pelvic posterior column fracture. Finally, different internal fixation models of the posterior acetabular column involving the quadrilateral area of the acetabulum were generated (Figure 3).
The upper surface of the sacrum was set as a rigid plane to simulate the sitting position and bipedal standing position under the human physiological state. The gravity of the upper half of the adult body was equivalent to a pressure of 600 N and uniformly loaded along the gravity axis. In the standing position, the lower end face of the femur was restrained, and the freedom of the six directions of the relevant nodes was set to zero to ensure that the plane composed of the bilateral anterior superior iliac spine and pubic symphysis was parallel to the gravity axis. Then, the stress and displacement distributions of the pelvis model in the standing position were calculated. In the sitting position, the bilateral ischial tubercle was restrained, and the freedom of the six directions of the relevant nodes was set to zero to ensure that the midpoint of the line between the lowest points of the bilateral ischial tubercles was perpendicular to the gravity axis. Then, the stress and displacement distributions of the pelvis model in the sitting position were calculated.
After the restraint and load were applied, ten points evenly distributed on the fracture line of the posterior column and quadrilateral area of the acetabulum in the acetabulum fossa were selected, and the stress and displacement data were measured in the sitting and standing positions. At the same time, the maximum stress and displacement of the ten points were obtained. Then, the displacement and stress distribution on the fracture line of the different internal fixation models were compared. In general, the more unstable the internal fixation, the greater the stress and displacement. The measurement indexes were: (1) The stiffness of the acetabulum structure was used to reflect the overall stability of the acetabulum after treatment of the fracture with different internal fixation; and (2) The stress distribution, the maximum value, and its position with different internal fixation methods were measured. According to the properties of the different materials, the mechanical characteristics were evaluated, and the possibility and location of failure of internal fixation were predicted.
Statistic Package for Social Science 22.0 (IBM Corp., Armonk, NY, United States) was used for statistical analysis. Continuous data conforming to the normal distribution (according to the Kolmogorov-Smirnov test) were presented as means ± SD, while those not conforming to the normal distribution were presented as medians (range). The mean values of stress and displacement at each point were compared among fixations. For the variable not normally distributed, the Kruskal-Wallis test was used, followed by the Dunnett-t post hoc test. For the indexes with a normal distribution, one-way analysis of variance and the Bonferroni post hoc test were used. P values < 0.05 indicated statistical significance.
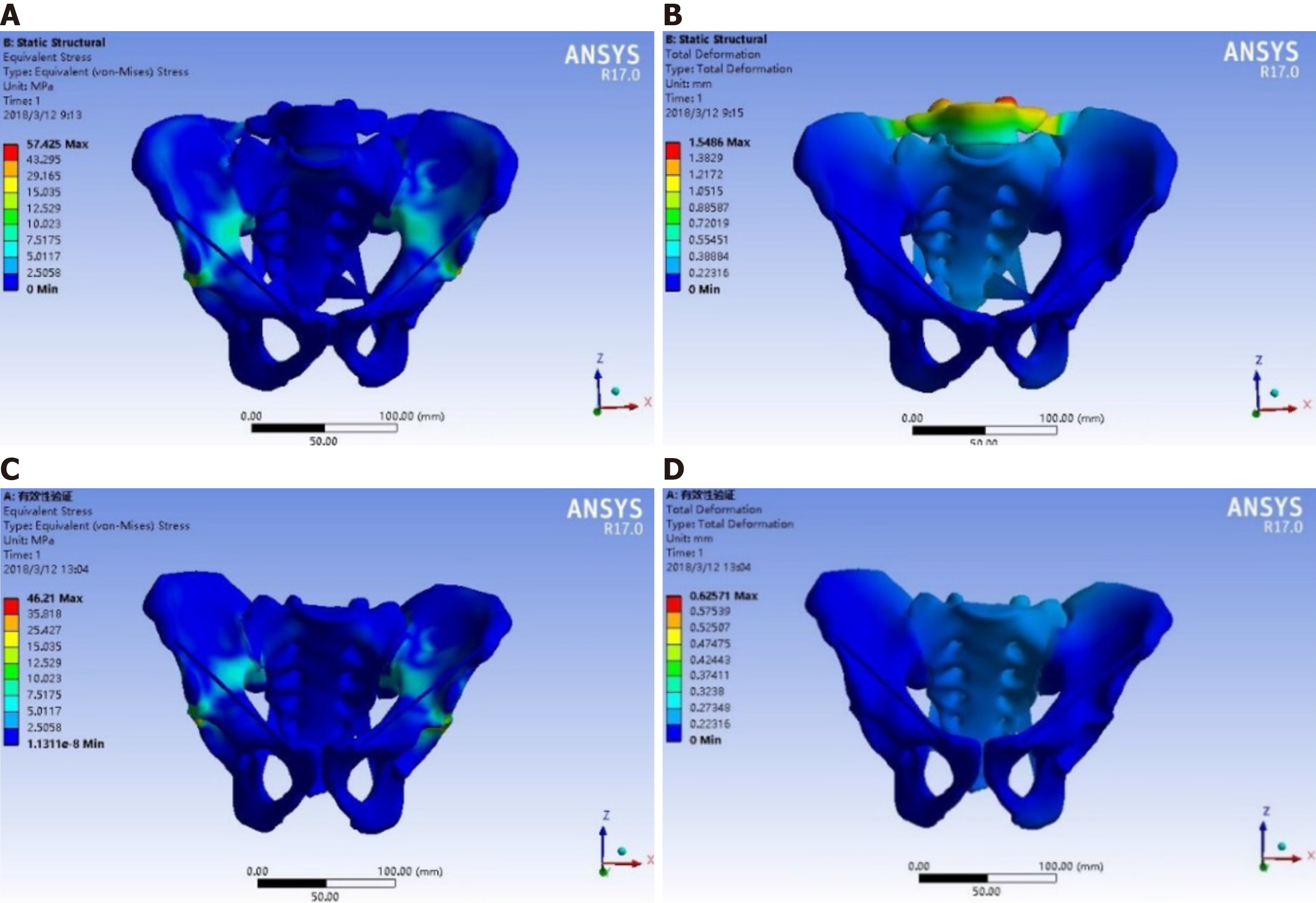
Figure 4 presents the validation of the simulation of the biomechanical conduction process. As can be seen by the colors on the model (dark blue indicating the smallest relative stress/displacement and red the highest), in the standing position, the stress applied on the sacral endplate was transmitted to the bilateral sacroiliac joints and ilium through the sacrum, backward and downward through the posterior acetabular column, forward through the medial arcuate edge of the pelvis to the pubic symphysis, and finally to the bilateral lower limbs through the hip joint. The maximum stress was 46.210 MPa. In the sitting position, the stress distribution of the pelvis was from top to bottom, and the sacrum bore the simulated gravity load at the upper end, which has a downward and forward displacement trend. The stress was mainly concentrated in the sacroiliac joint, posterior column, superior ischial branch, and pubic branch. The specific measurement data are shown in Supplementary Table
For the combined plate of the anterior and posterior columns in the sitting position, the stress on the fracture line was mainly concentrated in the middle of the acetabular fossa. The maximum stress was 2.296 MPa, the maximum displacement was 0.938 mm, and the average displacement was 0.604 ± 0.286 mm. In the standing position, the stress on the fracture line was mainly concentrated above the acetabulum. The maximum stress at each node of the fracture line was 1.880 MPa, the maximum displacement was 0.240 mm, and the average displacement was 0.140 ± 0.049 mm (Tables 2 and 3).
| Node | Combined steel plate | Internal iliac plate | Row nail blocking | Triangular steel plate | Spring steel plate | |||||
| Sitting | Standing | Sitting | Standing | Sitting | Standing | Sitting | Standing | Sitting | Standing | |
| 1 | 0.470 | 0.891 | 0.549 | 0.703 | 0.606 | 0.827 | 0.485 | 0.568 | 0.538 | 0.650 |
| 2 | 0.812 | 0.299 | 0.991 | 0.376 | 1.200 | 0.239 | 1.227 | 0.412 | 1.142 | 0.483 |
| 3 | 1.285 | 0.653 | 1.213 | 0.792 | 1.197 | 1.105 | 1.298 | 0.923 | 1.186 | 0.792 |
| 4 | 2.296 | 0.603 | 1.929 | 0.624 | 2.314 | 0.612 | 2.305 | 0.706 | 2.401 | 0.654 |
| 5 | 2.017 | 1.880 | 2.117 | 1.597 | 2.153 | 2.683 | 2.129 | 2.507 | 2.113 | 2.019 |
| 6 | 2.664 | 1.751 | 2.653 | 1.815 | 2.726 | 1.920 | 2.803 | 1.192 | 2.735 | 1.803 |
| 7 | 0.535 | 0.154 | 0.509 | 0.173 | 0.541 | 0.187 | 0.551 | 0.180 | 0.547 | 0.161 |
| 8 | 0.592 | 1.153 | 0.603 | 1.128 | 0.614 | 1.164 | 0.597 | 1.226 | 0.602 | 1.092 |
| 9 | 0.783 | 1.228 | 0.790 | 1.316 | 0.793 | 1.357 | 0.785 | 1.366 | 0.798 | 1.124 |
| 10 | 0.947 | 0.776 | 0.938 | 0.839 | 0.951 | 0.914 | 0.963 | 0.814 | 0.971 | 0.785 |
| Mean | 1.240 | 0.939 | 1.229 | 0.936 | 1.310 | 1.101 | 1.314 | 0.989 | 1.303 | 0.956 |
| SD | 0.757 | 0.541 | 0.708 | 0.497 | 0.756 | 0.719 | 0.778 | 0.618 | 0.772 | 0.547 |
| Minimum value | 0.470 | 0.154 | 0.509 | 0.173 | 0.541 | 0.187 | 0.485 | 0.180 | 0.538 | 0.161 |
| Maximum value | 2.296 | 1.880 | 2.653 | 1.815 | 2.726 | 2.683 | 2.803 | 2.507 | 2.735 | 2.019 |
| Node | Combined steel plate | Internal iliac plate | Row nail blocking | Triangular steel plate | Spring steel plate | |||||
| Sitting | Standing | Sitting | Standing | Sitting | Standing | Sitting | Standing | Sitting | Standing | |
| 1 | 0.097 | 0.089 | 0.085 | 0.099 | 0.087 | 0.103 | 0.093 | 0.107 | 0.102 | 0.141 |
| 2 | 0.910 | 0.103 | 0.481 | 0.086 | 0.956 | 0.097 | 0.914 | 0.105 | 1.104 | 0.127 |
| 3 | 0.938 | 0.112 | 0.458 | 0.102 | 0.683 | 0.124 | 0.832 | 0.120 | 1.017 | 0.136 |
| 4 | 0.104 | 0.093 | 0.484 | 0.128 | 1.109 | 0.115 | 0.753 | 0.098 | 0.936 | 0.128 |
| 5 | 0.887 | 0.121 | 0.401 | 0.157 | 0.990 | 0.131 | 0.914 | 0.144 | 1.125 | 0.205 |
| 6 | 0.682 | 0.117 | 0.377 | 0.128 | 0.887 | 0.135 | 0.756 | 0.126 | 0.913 | 0.146 |
| 7 | 0.652 | 0.129 | 0.473 | 0.172 | 0.633 | 0.153 | 0.671 | 0.167 | 0.801 | 0.182 |
| 8 | 0.556 | 0.194 | 0.503 | 0.172 | 0.545 | 0.201 | 0.539 | 0.187 | 0.714 | 0.214 |
| 9 | 0.520 | 0.198 | 0.588 | 0.171 | 0.511 | 0.198 | 0.597 | 0.178 | 0.618 | 0.201 |
| 10 | 0.690 | 0.239 | 0.590 | 0.241 | 0.538 | 0.244 | 0.702 | 0.237 | 0.843 | 0.257 |
| Mean | 0.604 | 0.140 | 0.444 | 0.146 | 0.694 | 0.150 | 0.677 | 0.147 | 0.817 | 0.171 |
| SD | 0.286 | 0.049 | 0.136 | 0.044 | 0.286 | 0.046 | 0.227 | 0.042 | 0.283 | 0.042 |
| Minimum value | 0.097 | 0.089 | 0.085 | 0.086 | 0.087 | 0.097 | 0.093 | 0.098 | 0.102 | 0.127 |
| Maximum value | 0.938 | 0.240 | 0.590 | 0.241 | 1.109 | 0.244 | 0.914 | 0.237 | 1.125 | 0.257 |
For the internal iliac plate in the sitting position, the stress on the fracture line of the left acetabulum was mainly concentrated in the anterior and superior acetabulum. The maximum stress at the fracture end was 2.653 MPa, the maximum displacement was 0.590 mm, and the average displacement was 0.444 ± 0.136 mm. In the standing position, the stress on the fracture line was mainly concentrated in the posterior and superior acetabulum. The maximum stress at each node of the fracture line was 1.815 MPa, the maximum displacement was 0.241 mm, and the average displacement was 0.146 ± 0.044 mm (Tables 2 and 3).
For the row nail blocking technology in the sitting position, the maximum stress at the fracture end of the left acetabulum was 2.726 MPa, the maximum displacement was 1.109 mm, and the average displacement was 0.694 ± 0.286 mm. In the standing position, the stress on the fracture line of the left acetabulum was mainly concentrated in the posterior and superior acetabulum. The maximum stress at each node of the fracture line was 2.683 MPa, the maximum displacement was 0.244 mm, and the average displacement was 0.150 ± 0.046 mm (Tables 2 and 3).
Regarding the triangle plate in the sitting position, the stress on the fracture line of the left acetabulum was mainly concentrated in the front and upper part of the joint. The maximum stress was 2.803 MPa, the maximum displacement was 0.914 mm, and the average displacement was 0.677 ± 0.227 mm. In the standing position, the stress on the fracture line of the left acetabulum was mainly concentrated in the upper part of the acetabulum. The maximum stress at each node of the fracture line was 2.507 MPa, the maximum displacement was 0.237 mm, and the average displacement was 0.147 ± 0.042 mm (Tables 2 and 3).
For the spring plate in the sitting position, the stress on the fracture line of the left acetabulum was mainly concentrated in the anterior part of the acetabulum. The maximum stress at the fracture end was 2.735 MPa, the maximum displacement was 1.125 mm, and the average displacement was 0.817 ± 0.283 mm. In the standing position, the stress was mainly concentrated in the posterior and upper part of the acetabulum. The maximum stress at each node of the fracture line was 2.019 MPa, the maximum displacement was 0.257 mm, and the average displacement was 0.171 ± 0.042 mm (Tables 2 and 3).
When comparing the five fixations, the results showed no statistically significant differences in the mean values of stress among the groups (sitting position: P = 0.9794; standing position: P = 0.9741) (Table 2). In terms of displacement, there was a statistically significant difference among the groups in the sitting position (P = 0.004), and the pairwise comparisons showed that the average displacement of the internal iliac plate group was significantly smaller than that of the spring plate group (P = 0.002), and no differences were observed between the other pairs of groups (all P > 0.05). In the standing position, there were no significant differences in the mean value of displacement among the groups (P = 0.2985) (Table 3).
It can be seen from the stress nephogram of the internal fixations in different positions that the stress of the internal fixation was mainly concentrated in the fracture segment, indicating that the internal fixations had considerable stress on the fracture segment, and the possibility of internal fixation failure was relatively high in this part (Figure 5).
The standing and sitting positions are the most physiological postures in daily human life. Therefore, in this study the stability of the fixation of the acetabulum posterior column fracture involving the quadrilateral area of the acetabulum was analyzed with each internal fixator in the standing and sitting positions. The results suggest no significant differences among the fixations for the acetabular posterior column fracture involving the quadrilateral area of the acetabulum. The fixation effect of the spring plate was relatively poor.
Of course, the pressure load was different in the standing and sitting positions. Indeed, in the standing position, the stress applied on the sacral endplate was transmitted to the bilateral sacroiliac joints and ilium through the sacrum, backward and downward through the posterior acetabular column, forward through the medial arcuate edge of the pelvis to the pubic symphysis, and finally to the bilateral lower limbs through the hip joint. In the sitting position, the stress distribution of the pelvis was from top to bottom, and the sacrum bore the simulated gravity load at the upper end, which had a downward and forward displacement trend. The stress was mainly concentrated in the sacroiliac joint, posterior column, superior ischial branch, and pubic branch. Those measurements were in concordance with what was expected from those positions as supported by previous studies[22,26,27].
In this study, the spring plate fixation showed a worse effect than the other fixation methods. It might be because the distal end of the plate cannot be fixed with screws, and the displacement of the distal end cannot be controlled. If the steel plate is over shaped when the steel plate is placed, then the steel plate near the pelvic edge will not fit the bone surface. There were no significant differences among the combined plate, internal iliac plate, row nail blocking, and triangle plate fixation for acetabulum posterior column fracture involving the quadrilateral area of the acetabulum. Those results might suggest that those four fixation devices can be used interchangeably, but their specific application should be combined according to each patient’s clinical and individual conditions.
Various studies used a finite element model to assess the impact of different fixation devices for hip fractures. Fan et al[28] compared the double-column reconstruction plate, the anterior column plate combined with posterior column screws, and the anterior column plate combined with quadrilateral area screws in T-shaped acetabular fractures and showed that the anterior column plate combined with quadrilateral area screws achieved the best outcomes in terms of pressure and displacement. Using a similar approach, Lei et al[29] compared the same three fixations except for hemitransverse acetabular fractures and showed that the anterior column plate combined with quadrilateral area screws also achieved the best outcomes. Yildirim et al[30] suggested that anterior or posterior column screws were superior to two-column support for transverse acetabular fracture. The direct comparison of those three studies with the present one is difficult because of the differences in fracture types. Nevertheless, the present study suggests that the internal iliac plate resulted in the smallest displacement in the sitting position.
The present study has limitations. The finite element model has shortcomings. Because of the complex structure of the pelvis and acetabulum, the thickness of the cortical bone and the amount of cancellous bone are different between each bone block and different parts of the same bone block, and there are also differences between different individuals. Therefore, it is inevitable to observe errors compared with clinical practice when assigning an elastic modulus and Poisson’s ratio to a specific bone block. Second, in terms of a simplified model, this experiment includes the reconstruction of muscles and ligaments. When modeling, because of the use of the spring element to simulate a ligament, there is a large stress concentration on the surface of the cortical bone in the pelvis model, which has a certain error with the actual reality of the solid pelvis[31]. In this study, it is assumed that the materials involved are continuous and homogeneous, which is not consistent with the characteristics of non-uniformity, heterogeneity, and nonlinearity found in actual human tissues. Due to the computing limitations, it is impossible to analyze every point on the fracture line, so there are some differences between the experimental results and reality. In addition, a fracture of the quadrilateral area of the acetabulum is often comminuted, which is challenging to simulate. Finally, the model was constructed from a single healthy volunteer. Because hip fractures are more frequent in elderly and osteoporotic women, future studies should also examine those patient types and make comparisons among them.
In conclusion, ten points on the fracture line of the posterior column and quadrilateral area of the acetabulum in the acetabulum fossa were measured for stress and displacement data in the sitting position and standing position using five different fixation devices. There were no significant differences among the fixations for the acetabular posterior column fracture involving the quadrilateral area of the acetabulum. The fixation effect of the spring plate was relatively poor, while the internal iliac plate resulted in the smallest displacement in the sitting position. The results provide a basis for the biomechanical characteristics of acetabular posterior column fracture fixation.
With the modernization of society and transportation in the last several decades in China, the incidence of high-energy trauma, including acetabular fractures, has increased sharply in China.
The treatment of acetabular fractures is challenging, especially for fractures of the quadrilateral area. Obtaining a three-dimensional finite element model of the pelvis is an effective method for biomechanical research and can provide a basis for the biomechanical characteristics of different fixation methods applied in acetabular posterior column fracture.
This study aimed to establish different finite element models (in simulated standing and sitting positions) of the internal iliac plate, combined plate of anterior and posterior columns, triangle plate, row nail blocking, and spring plate for acetabular posterior column fractures involving the quadrilateral area of the acetabulum.
The three-dimensional models of the normal and fractured pelvis and the five internal fixations were established using computed tomography data of the pelvis of a living volunteer.
In the standing position, the maximum stress was 46.210 MPa. In the sitting position, the sacrum bore the simulated gravity load at the upper end. When comparing the five fixations, there were no significant differences in the stress mean values among groups. The average displacement of the internal iliac plate group was smaller than that of the spring plate group, and no differences were observed between the other pairs of groups. In the standing position, there were no significant differences in the mean value of displacement among the groups. Of note, the data were obtained from the model constructed from a single individual. The results should be validated in multiple individuals.
There were no significant differences among the fixations for acetabular posterior column fractures involving the quadrilateral area of the acetabulum.
The results provide a basis for the biomechanical characteristics of acetabular posterior column fracture fixation. Nevertheless, future studies should examine patients with different characteristics (e.g., elderly, female, or osteoporotic) and patients with different types of fractures because simple posterior column fracture is not commonly seen, and this fracture model cannot satisfy the biomechanical studies of all kinds of posterior column fractures.
Manuscript source: Unsolicited manuscript
Specialty type: Medicine, research and experimental
Country/Territory of origin: China
Peer-review report’s scientific quality classification
Grade A (Excellent): 0
Grade B (Very good): B
Grade C (Good): C
Grade D (Fair): 0
Grade E (Poor): 0
P-Reviewer: Corrales FJ, Shimizu Y S-Editor: Zhang L L-Editor: Filipodia P-Editor: Wang LL
| 1. | Stevens JA, Rudd RA. The impact of decreasing U.S. hip fracture rates on future hip fracture estimates. Osteoporos Int. 2013;24:2725-2728. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 144] [Cited by in RCA: 166] [Article Influence: 13.8] [Reference Citation Analysis (0)] |
| 2. | Brauer CA, Coca-Perraillon M, Cutler DM, Rosen AB. Incidence and mortality of hip fractures in the United States. JAMA. 2009;302:1573-1579. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1153] [Cited by in RCA: 1218] [Article Influence: 76.1] [Reference Citation Analysis (0)] |
| 3. | Mauffrey C, Hao J, Cuellar DO 3rd, Herbert B, Chen X, Liu B, Zhang Y, Smith W. The epidemiology and injury patterns of acetabular fractures: are the USA and China comparable? Clin Orthop Relat Res. 2014;472:3332-3337. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 61] [Cited by in RCA: 66] [Article Influence: 6.0] [Reference Citation Analysis (0)] |
| 4. | LeBlanc KE, Muncie HL Jr, LeBlanc LL. Hip fracture: diagnosis, treatment, and secondary prevention. Am Fam Physician. 2014;89:945-951. [PubMed] |
| 5. | Chung TC, Chen TS, Hsu YC, Kao FC, Tu YK, Liu PH. Long-term total hip arthroplasty rates in patients with acetabular and pelvic fractures after surgery: A population-based cohort study. PLoS One. 2020;15:e0231092. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 1] [Cited by in RCA: 2] [Article Influence: 0.4] [Reference Citation Analysis (0)] |
| 6. | Xia WB, He SL, Xu L, Liu AM, Jiang Y, Li M, Wang O, Xing XP, Sun Y, Cummings SR. Rapidly increasing rates of hip fracture in Beijing, China. J Bone Miner Res. 2012;27:125-129. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 132] [Cited by in RCA: 159] [Article Influence: 12.2] [Reference Citation Analysis (0)] |
| 7. | Peter RE. Open reduction and internal fixation of osteoporotic acetabular fractures through the ilio-inguinal approach: use of buttress plates to control medial displacement of the quadrilateral surface. Injury. 2015;46 Suppl 1:S2-S7. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 41] [Cited by in RCA: 47] [Article Influence: 4.7] [Reference Citation Analysis (0)] |
| 8. | Florschutz AV, Langford JR, Haidukewych GJ, Koval KJ. Femoral neck fractures: current management. J Orthop Trauma. 2015;29:121-129. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 174] [Cited by in RCA: 255] [Article Influence: 25.5] [Reference Citation Analysis (0)] |
| 9. | Sagi HC, Afsari A, Dziadosz D. The anterior intra-pelvic (modified rives-stoppa) approach for fixation of acetabular fractures. J Orthop Trauma. 2010;24:263-270. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 146] [Cited by in RCA: 164] [Article Influence: 10.9] [Reference Citation Analysis (0)] |
| 10. | Hirvensalo E, Lindahl J, Böstman O. A new approach to the internal fixation of unstable pelvic fractures. Clin Orthop Relat Res. 1993: 28-32. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 45] [Cited by in RCA: 53] [Article Influence: 1.7] [Reference Citation Analysis (0)] |
| 11. | Farid YR. Cerclage wire-plate composite for fixation of quadrilateral plate fractures of the acetabulum: a checkrein and pulley technique. J Orthop Trauma. 2010;24:323-328. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 38] [Cited by in RCA: 44] [Article Influence: 2.9] [Reference Citation Analysis (0)] |
| 12. | Tile M. Fractures of the pelvis and acetabulum. 2nd ed. Baltimore: Williams & Wilkins, 1995. |
| 13. | Judet R, Judet J, Letournel E. Fractures of The Acetabulum: Classification and Surgical Approaches For Open Reduction. Preliminary Report. J Bone Joint Surg Am. 1964;46:1615-1646. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 800] [Cited by in RCA: 730] [Article Influence: 25.2] [Reference Citation Analysis (0)] |
| 14. | Scheinfeld MH, Dym AA, Spektor M, Avery LL, Dym RJ, Amanatullah DF. Acetabular fractures: what radiologists should know and how 3D CT scan aid classification. Radiographics. 2015;35:555-577. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 62] [Cited by in RCA: 51] [Article Influence: 5.7] [Reference Citation Analysis (0)] |
| 15. | Wu YD, Cai XH, Liu XM, Zhang HX. Biomechanical analysis of the acetabular buttress-plate: are complex acetabular fractures in the quadrilateral area stable after treatment with anterior construct plate-1/3 tube buttress plate fixation? Clinics (Sao Paulo). 2013;68:1028-1033. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 23] [Cited by in RCA: 26] [Article Influence: 2.2] [Reference Citation Analysis (0)] |
| 16. | Zha GC, Sun JY, Dong SJ, Zhang W, Luo ZP. A novel fixation system for acetabular quadrilateral plate fracture: a comparative biomechanical study. Biomed Res Int. 2015;2015:391032. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 11] [Cited by in RCA: 15] [Article Influence: 1.5] [Reference Citation Analysis (0)] |
| 17. | Douraiswami B, Vinayak G. Isolated Quadrilateral Plate Fracture of the Acetabulum - a unique case Scenario. J Orthop Case Rep. 2012;2:32-34. [PubMed] |
| 18. | Laflamme GY, Hebert-Davies J, Rouleau D, Benoit B, Leduc S. Internal fixation of osteopenic acetabular fractures involving the quadrilateral plate. Injury. 2011;42:1130-1134. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 114] [Cited by in RCA: 127] [Article Influence: 9.1] [Reference Citation Analysis (0)] |
| 19. | Qureshi AA, Archdeacon MT, Jenkins MA, Infante A, DiPasquale T, Bolhofner BR. Infrapectineal plating for acetabular fractures: a technical adjunct to internal fixation. J Orthop Trauma. 2004;18:175-178. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 86] [Cited by in RCA: 87] [Article Influence: 4.1] [Reference Citation Analysis (0)] |
| 20. | Losco M, Familiari F, Giron F, Papalia R. Use and Effectiveness of the Cadaver-Lab in Orthopaedic and Traumatology Education: An Italian Survey. Joints. 2017;5:197-201. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 8] [Cited by in RCA: 14] [Article Influence: 1.8] [Reference Citation Analysis (0)] |
| 21. | Matuszewski S, Hall MJR, Moreau G, Schoenly KG, Tarone AM, Villet MH. Pigs vs people: the use of pigs as analogues for humans in forensic entomology and taphonomy research. Int J Legal Med. 2020;134:793-810. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 57] [Cited by in RCA: 111] [Article Influence: 18.5] [Reference Citation Analysis (0)] |
| 22. | Zhang L, Peng Y, Du C, Tang P. Biomechanical study of four kinds of percutaneous screw fixation in two types of unilateral sacroiliac joint dislocation: a finite element analysis. Injury. 2014;45:2055-2059. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 39] [Cited by in RCA: 46] [Article Influence: 4.2] [Reference Citation Analysis (0)] |
| 23. | Wako Y, Nakamura J, Matsuura Y, Suzuki T, Hagiwara S, Miura M, Kawarai Y, Sugano M, Nawata K, Yoshino K, Orita S, Inage K, Ohtori S. Finite element analysis of the femoral diaphysis of fresh-frozen cadavers with computed tomography and mechanical testing. J Orthop Surg Res. 2018;13:192. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 8] [Cited by in RCA: 11] [Article Influence: 1.6] [Reference Citation Analysis (0)] |
| 24. | Jacob HA, Huggler AH, Dietschi C, Schreiber A. Mechanical function of subchondral bone as experimentally determined on the acetabulum of the human pelvis. J Biomech. 1976;9:625-627. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 83] [Cited by in RCA: 60] [Article Influence: 1.2] [Reference Citation Analysis (0)] |
| 25. | Lin SQ, Wang B, Zhang L, Yang CJ. Application and research progress of finite element analysis in orthopaedics. Zhongguo Zhongyi Gushangke Zazhi. 2013;21:69-73. [DOI] [Full Text] |
| 26. | Li Z, Kim JE, Davidson JS, Etheridge BS, Alonso JE, Eberhardt AW. Biomechanical response of the pubic symphysis in lateral pelvic impacts: a finite element study. J Biomech. 2007;40:2758-2766. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 75] [Cited by in RCA: 72] [Article Influence: 4.0] [Reference Citation Analysis (0)] |
| 27. | Anderson AE, Peters CL, Tuttle BD, Weiss JA. Subject-specific finite element model of the pelvis: development, validation and sensitivity studies. J Biomech Eng. 2005;127:364-373. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 252] [Cited by in RCA: 243] [Article Influence: 12.2] [Reference Citation Analysis (0)] |
| 28. | Fan Y, Lei J, Zhu F, Li Z, Chen W, Liu X. Biomechanical Analysis of the Fixation System for T-Shaped Acetabular Fracture. Comput Math Methods Med. 2015;2015:370631. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 17] [Cited by in RCA: 17] [Article Influence: 1.7] [Reference Citation Analysis (0)] |
| 29. | Lei J, Dong P, Li Z, Zhu F, Wang Z, Cai X. Biomechanical analysis of the fixation systems for anterior column and posterior hemi-transverse acetabular fractures. Acta Orthop Traumatol Turc. 2017;51:248-253. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 17] [Cited by in RCA: 26] [Article Influence: 3.3] [Reference Citation Analysis (0)] |
| 30. | Yildirim AO, Alemdaroglu KB, Yuksel HY, Öken ÖF, Ucaner A. Finite element analysis of the stability of transverse acetabular fractures in standing and sitting positions by different fixation options. Injury. 2015;46 Suppl 2:S29-S35. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 16] [Cited by in RCA: 24] [Article Influence: 2.4] [Reference Citation Analysis (0)] |
| 31. | Phillips AT, Pankaj P, Howie CR, Usmani AS, Simpson AH. Finite element modelling of the pelvis: inclusion of muscular and ligamentous boundary conditions. Med Eng Phys. 2007;29:739-748. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 155] [Cited by in RCA: 168] [Article Influence: 8.8] [Reference Citation Analysis (0)] |