Leveraging machine learning techniques for predicting pancreatic neuroendocrine tumor grades using biochemical and tumor markers

Abstract

BACKGROUND

The incidence of pancreatic neuroendocrine tumors (PNETs) is now increasing rapidly. The tumor grade of PNETs significantly affects the treatment strategy and prognosis. However, there is still no effective way to non-invasively classify PNET grades. Machine learning (ML) algorithms have shown potential in improving the prediction accuracy using comprehensive data.

AIM

To provide a ML approach to predict PNET tumor grade using clinical data.

METHODS

The clinical data of histologically confirmed PNET cases between 2012 and 2018 were collected. A method of minimum P for the Chi-square test was used to divide the continuous variables into binary variables. The continuous variables were transformed into binary variables according to the cutoff value, while the P value was minimum. Four classical supervised ML models, including logistic regression, support vector machine (SVM), linear discriminant analysis (LDA) and multi-layer perceptron (MLP) were trained by clinical data, and the models were labeled with the pathological tumor grade of each PNET patient. The performance of each model, including the weight of the different parameters, were evaluated.

RESULTS

In total, 91 PNET cases were included in this study, in which 32 were G1, 48 were G2 and 11 were G3. The results showed that there were significant differences among the clinical parameters of patients with different grades. Patients with higher grades tended to have higher values of total bilirubin, alpha fetoprotein, carcinoembryonic antigen, carbohydrate antigen 19-9 and carbohydrate antigen 72-4. Among the models we used, LDA performed best in predicting the PNET tumor grade. Meanwhile, MLP had the highest recall rate for G3 cases. All of the models stabilized when the sample size was over 70 percent of the total, except for SVM. Different parameters varied in affecting the outcomes of the models. Overall, alanine transaminase, total bilirubin, carcinoembryonic antigen, carbohydrate antigen 19-9 and carbohydrate antigen 72-4 affected the outcome greater than other parameters.

CONCLUSION

ML could be a simple and effective method in non-invasively predicting PNET grades by using the routine data obtained from the results of biochemical and tumor markers.

Key Words: Machine learning, Pancreatic neuroendocrine tumors, Tumor grade, Biochemical indexes, Tumor markers

Core tip: In this study, we provide a machine learning approach to predict the grade of pancreatic neuroendocrine tumors (PNETs) using combined clinical data. We design a method of minimum P for the Chi-square test to maximize differences between groups, which benefited the model’s construction. Then, we proposed four classical supervised machine learning models by using biochemical and tumor markers. After the tuning, training and testing of the models, we made sure that the trained models gave stable results. In general, the result of our study provided a non-invasive way to judge the condition of PNETs and offers a reference for treatment.

INTRODUCTION

Pancreatic neuroendocrine tumors (PNETs) comprise a heterogeneous group of neoplasms[1-3], and different types of neoplasms have various clinical features. Although PNETs are still rare and account for only 1%-3% of all primary pancreatic malignancies, its incidence has increased 700% in the past 30 years, partly due to an increasing diagnostic rate[4,5].

To establish a standard classification system that can reflect the prognosis of PNETs, the World Health Organization (WHO) defined a system based on pathology examination that divided PNETs into three grades according to the mitotic rate and Ki67 index[6]. Generally, a higher grade indicates a worse prognosis[7]. Moreover, the PNET grade may greatly affect the treatment program. The PNET grade can only be obtained from pathological reports after undergoing puncture biopsy or surgery. However, biopsy is relatively limited due to additional invasion and needle tract implantation metastases, and the positive results are largely dependent on the physical condition of patients and the experience of operators. Surgery is another effective way to obtain a specimen, but the operation indication for PNETs has been very limited[8]. Furthermore, it would have a guidance meaning for the surgical resection range if the tumor grade is known before surgery. Therefore, it would be very meaningful to develop a method that could non-invasively predict the PNET grade.

Machine learning (ML) has rapidly developed in recent years and is now widely used in many fields[9]. ML has provided an approach to an accurate classification system for complex parameters and disease outcomes, such as cancer and cardio-vascular disease[10-12]. In this study, we used four ML classification algorithms to determine the relationship between conventional serological examination indexes and the pathological tumor grade of PNETs. Each classifier was trained by using routine examinations on admission to develop a specific and practical model that can non-invasively predict PNET grades.

MATERIALS AND METHODS

Patient population

Ninety-one patients who had undergone enucleation, distal pancreatectomy or pancreaticoduodenectomy between January 1, 2013 and December 31, 2018 in the Second Department of Hepatobiliary Surgery at the PLA General Hospital were included in this study. All of the patients received the final surgical pathology diagnosis of PNETs. Pathological examinations were used to confirm the PNET grades. The serum levels of alanine transaminase (ALT), total bilirubin (BIL), alpha fetoprotein (AFP), carcinoembryonic antigen (CEA), carbohydrate antigen 19-9 (CA19-9), carbohydrate antigen 15-3 (CA15-3) and carbohydrate antigen 72-4 (CA72-4) were measured within 3 d before the operation. The corresponding clinical data were retrieved from the electronic database. The study protocol was approved by the Ethics Committee of the PLA General Hospital and was performed in accordance with the ethical standards as established in the 1964 Declaration of Helsinki and its later amendments or comparable ethical standards. Additionally, all patients signed a consent form to participate in this study.

Sample pre-processing

A minimum P value for the Chi-square test (MPCST) method was used to transform continuous variables into binary variables in the following steps. Firstly, a cutoff value for each variable value was selected in numerical order. For each cutoff value, if a variable value was greater than or equal to the cutoff value, it was labeled “1”, otherwise, the value was labeled “0”. Then, the variable was analyzed by Chi-square test to calculate the P value. Lastly, the variable was transformed into binary variables according to the cutoff value when the P value was at its minimum.

Classifiers

Python 3.6.0 (Anaconda 4.3.0), which included scikit-learn 0.19.0, was used to make the classification models. Four supervised classifiers were selected in this study: logistic regression (LR), support vector machine (SVM), linear discriminant analysis (LDA) and multilayer perceptron (MLP). LR predicts the binary response probability for the outcome class given the values of predictors. The magnitude of the C -values from the LR was used as a predictor of importance rank[13]. We used SVM with a solver of radial basis function kernel or a linear function kernel. Both were defined by C, or the misclassification cost. We tuned C by performing a logarithmic grid search between 1 × 10^-5 and 1 × 10⁴. Unbalance between the classes was adjusted by setting the class_weight parameter to balanced[14]. LDA is based on a linear combination of input features. It has three possible solvers: singular value decomposition (svd), least square solution (lsqr), and eigenvalue decomposition (eigen). The shrinkage parameter significantly affects the outcome of LDA[15]. MLP is a model that simulates how neurons works. The data was weighted and propagated to the next layer, which includes several nodes, and at last propagated to the output layer. Then, the weight of each node in each layer was adjusted according to the error value.

Performance measures and statistical testing

We tested and reported four indexes of each task for evaluating the performance of models, including precision rate, recall rate, and F1-score. The three indexes are explained and listed in Table 1.

Table 1 General confusion matrix.

		Predicted condition
		Predicted negative	Predicted positive
Condition	Condition negative	True negative	False positive
	Condition positive	False negative	True positive

The following formulas were used to define the four measures: (1) Precision rate = true positive (TP) / (TP + false positive (FP)); (2) Recall rate = true negative (TN) / (TP + false negative (FN)); and (3) F1 score = (2 × Precision × Recall) / (Precision + Recall).

We used a two-step approach to build the classifier. In the first step, G1 was labeled “negative”, G2 and G3 were labeled “positive”. Then, in the second step, G1 and G2 were labeled “negative”, G3 was labeled “positive”. Every classifier was used successively in the two steps. If the result we got from the two steps were both “positive”, the sample was regarded as G3; if a sample was classified as “positive” in step 1 but “negative” in step 2, it was regarded as G2; if a sample was classified as “negative” in both steps, the sample was regarded as G1.

The leave-one-out cross-validation setup[16] was used to train and test the classifier. In brief, each sample (patient) will be treated as test sample, trained by data set of size n-1, while n is the total sample size. The procedure will be repeated for 100 times. In the end, each sample will be assigned to one of the classes according to majority voting. This process will be repeated until all patients from each task have been tested.

Additional statistics

We present Gaussian continuous variables as the mean ± SD and categorical variables as ratios. For univariate class comparisons, we used Welch’s t-test for Gaussian continuous variables and Pearson’s χ²-test for categorical variables. All of the statistical analyses were performed using IBM^® SPSS 19.0 software. The statistical significance threshold was set to 5% for two-tailed tests. All the statistical review of the study was performed by a biomedical statistician from the Institute of Medical Management of Chinese PLA General Hospital.

RESULTS

Relationship between different clinical parameters and PNET grade

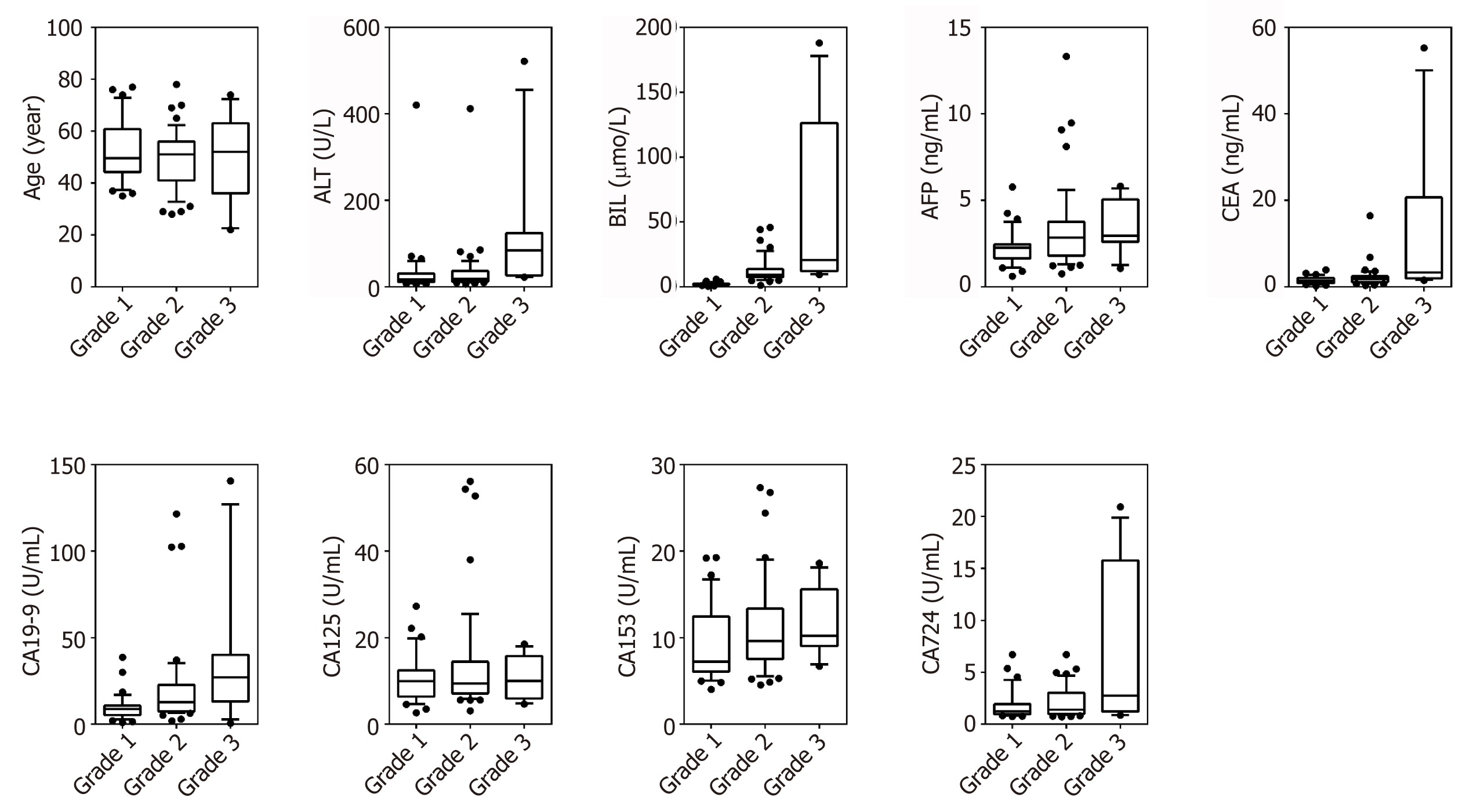
Ninety-one patients were included in the analysis with G1 (n = 32), G2 (n = 48), G3 (n = 11). Data on gender, age, ALT, BIL, AFP, CEA, CA19-9, CA15-3 and CA72-4 were collected. Figure 1 shows boxplots comparing the factors between different groups. The relationship between groups and various clinical pathological parameters is listed in Table 2. Significant differences were found in ALT, BIL, AFP, CEA, CA19-9, CA125 and CA72-4 between G3 and G1; in gender, age, BIL, CEA and CA72-4 between G3 and G2; and in gender, BIL, AFP, CA19-9 and CA125 between G2 and G1. The results showed that patients with higher grades tend to have higher values of BIL, AFP, CEA, CA19-9 and CA72-4.

Figure 1 Distribution of different clinical variables.

Table 2 Relationship between different pancreatic neuroendocrine tumor grades and clinical variables.

	mean ± SD	P value, vs G1	P value, vs G2	P value of binary
Gender (male / female)			s	0.3575
G1	14 / 18
G2	37 / 11	0.002
G3	4 / 7	0.668	0.008
Age				< 0.001
G1	52.47 ± 11.70
G2	49.19 ± 11.34	0.634
G3	50.00 ± 17.04	0.082	0.039
ALT				< 0.001
G1	34.95 ± 72.06
G2	33.97 ± 59.10	0.730
G3	117.02 ± 143.74	0.039	0.006
BIL				< 0.001
G1	9.15 ± 3.65
G2	12.71 ± 9.56	0.009
G3	69.63 ± 67.56	< 0.001	< 0.001
AFP				< 0.001
G1	2.27 ± 1.02
G2	3.34 ± 2.38	0.014
G3	3.47 ± 1.50	0.035	0.606
CEA				< 0.001
G1	1.51 ± 0.82
G2	2.19 ± 2.38	0.132
G3	11.77 ± 17.05	< 0.001	< 0.001
CA19-9				< 0.001
G1	9.58 ± 7.57
G2	20.46 ± 24.74	0.007
G3	37.10 ± 39.40	< 0.001	0.118
CA125				0.0146
G1	10.43 ± 5.60
G2	13.72 ± 12.22	0.039
G3	11.13 ± 4.75	0.942	0.195
CA15-3				< 0.001
G1	8.98 ± 4.34
G2	11.41 ± 5.49	0.361
G3	11.52 ± 3.80	0.585	0.318
CA72-4				< 0.001
G1	1.83 ± 1.43
G2	2.14 ± 1.50	0.217
G3	7.42 ± 7.85	< 0.001	< 0.001

BIL: Bilirubin; ALT: Alanine transaminase; CA: Carbohydrate antigen; CEA: Carcinoembryonic antigen; AFP: Alpha fetoprotein.

Model tuning, training and testing

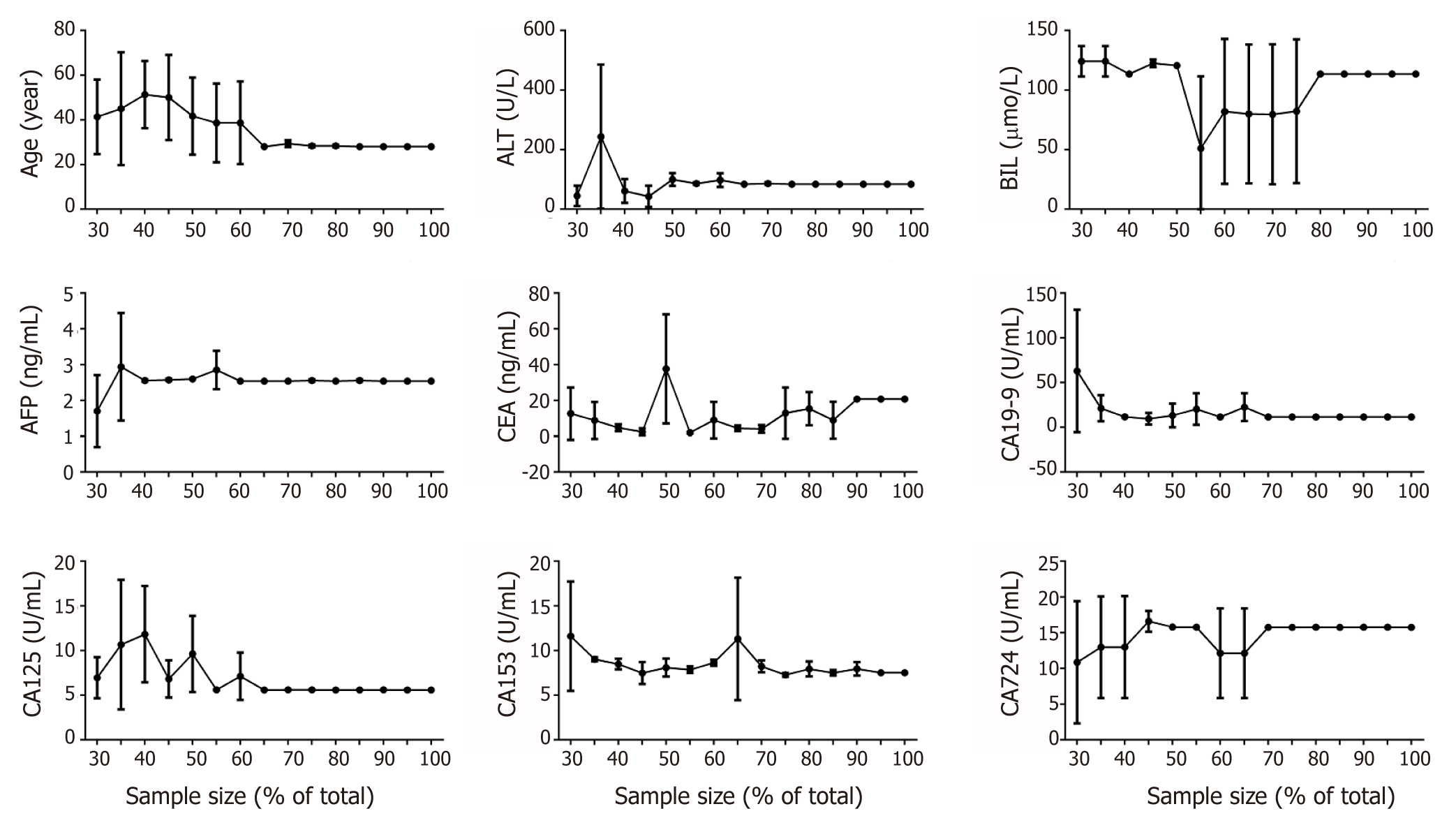
The data were pre-processed with the MPCST method. For robustness check, 30% to 100% of the total samples were selected randomly. We determined the optimal cut-off value by calculating the minimum P value (Figure 2). It was found that all of the parameters had a stable cutoff value when the sample size is over 70% of total, except BIL (over 80%) and CEA (> 90%). According to these cutoff values, all of the parameters were transformed into binary variables for further analysis.

Figure 2 The cutoff value with the minimum P for Chi-square test when sample volume ranged from 30% to 100% in steps of 5%.

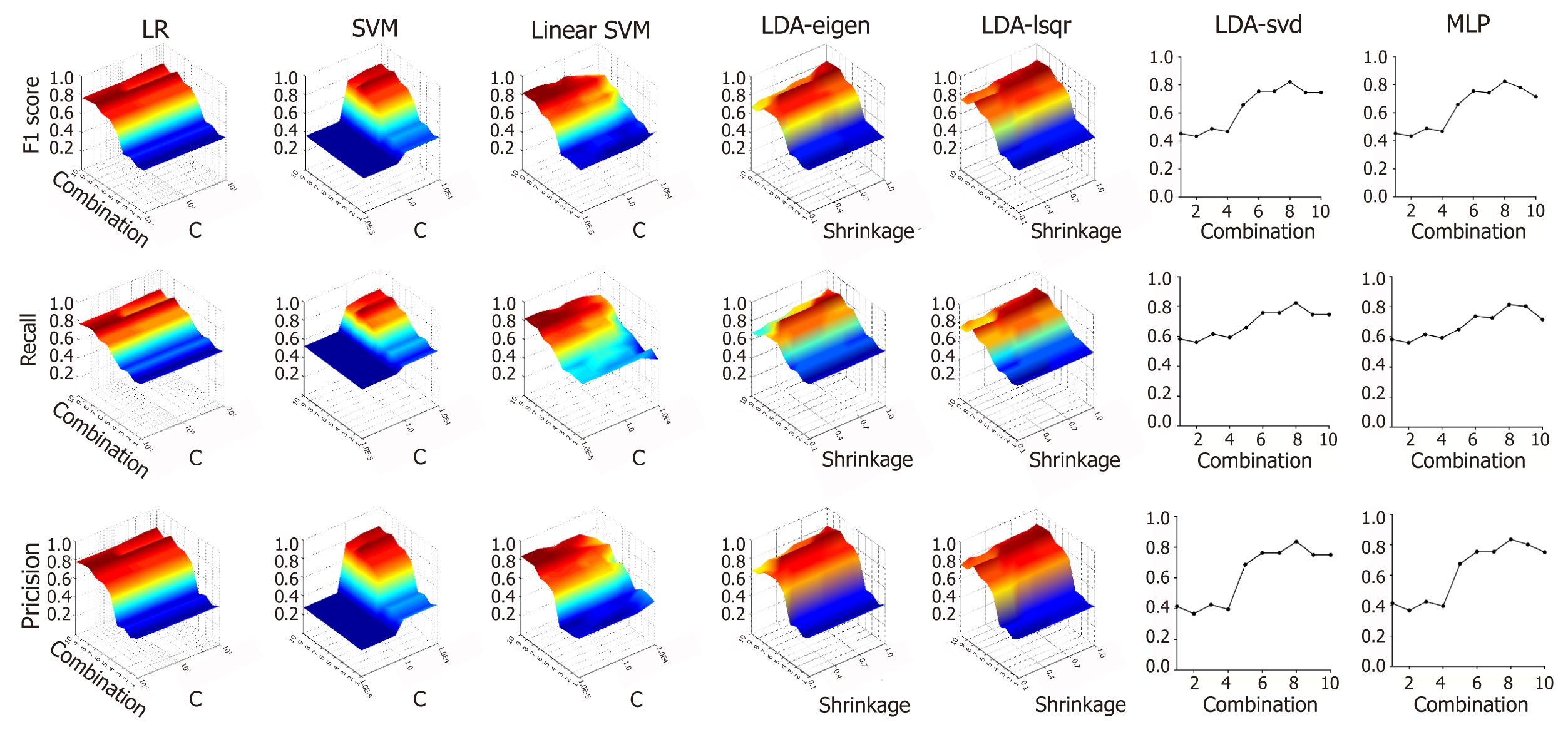
Figure 3 shows the effect of different variable combinations and parameters on f1 score, recall rate and precision rate. Training was performed on ten different combinations of variables to evaluate the classification power of clinical data. For Linear SVM, the f1 score, recall rate and precision rate were the highest when using all ten clinical indicators as independent variables. For SVM, LR, MLP and LDA with three different solvers, the scores were highest when using a combination of age, ALT, BIL, AFP, CEA, CA19-9, CA15-3 and CA72-4 as independent variables. The value of C greatly affected the performance of SVM and Linear SVM. SVM performed the best when C was equal to 1, and Linear SVM performed the best when C was equal to 0.00001. However, the value of C did not affect the performance of LR. For LDA, the “shrinkage” parameter significantly affects the outcome of the models. The models showed the highest classification power when the shrinkage value was 0.90 in LDA-eigen and 1 in LDA-lsqr.

Figure 3 The impact of a combination of independent variables and change of parameter on F1 score, recall rate and precision rate of four models. Combination 1: bilirubin (BIL); 2: BIL + alanine transaminase (ALT); 3: BIL + ALT + carbohydrate antigen 72-4 (CA72-4); 4: BIL + ALT + CA72-4 + carcinoembryonic antigen (CEA); 5: BIL + ALT + CA72-4 + CEA + CA19-9; 6: BIL + ALT + CA72-4 + CEA + CA19-9 + alpha fetoprotein (AFP); 7: BIL + ALT + CA72-4 + CEA + CA19-9 + AFP + age; 8: BIL + ALT + CA72-4 + CEA + CA19-9 + AFP + age + CA15-3; 9: BIL + ALT + CA72-4 + CEA + CA19-9 + AFP + age + CA15-3 + CA125; 10: BIL + ALT + CA72-4 + CEA + CA19-9 + AFP + age + CA15-3 + CA125 + gender). LR: Logistic regression; SVM: Support vector machine; LDA: Linear discriminant analysis MLP: Multilayer perceptron.

Table 3 shows the classification power of different models using the optimum parameter combination. The result showed that LDA performed the best in classification. The highest f1 score, recall rate and precision rate for LDA was 0.85, 0.85 and 0.86, respectively. The result is unrelated with the solver. For other models, the f1 scores and recall rate ranged from 0.80 to 0.82, and the precision rate ranged from 0.81 to 0.84.

Table 3 The highest F1 score, recall rate and precision rate scores of different models.

	F1 score	Recall rate	Precision rate
LR	0.80	0.80	0.81
SVM	0.81	0.81	0.82
Linear SVM	0.82	0.82	0.84
LDA-eigen1	0.85	0.85	0.86
LDA-lsqr1	0.85	0.85	0.86
LDA-svd	0.82	0.82	0.84
MLP	0.82	0.81	0.84

¹Values over 0.85. LR: Logistic regression; SVM: Support vector machine; LDA: Linear discriminant analysis; MLP: Multilayer perceptron.

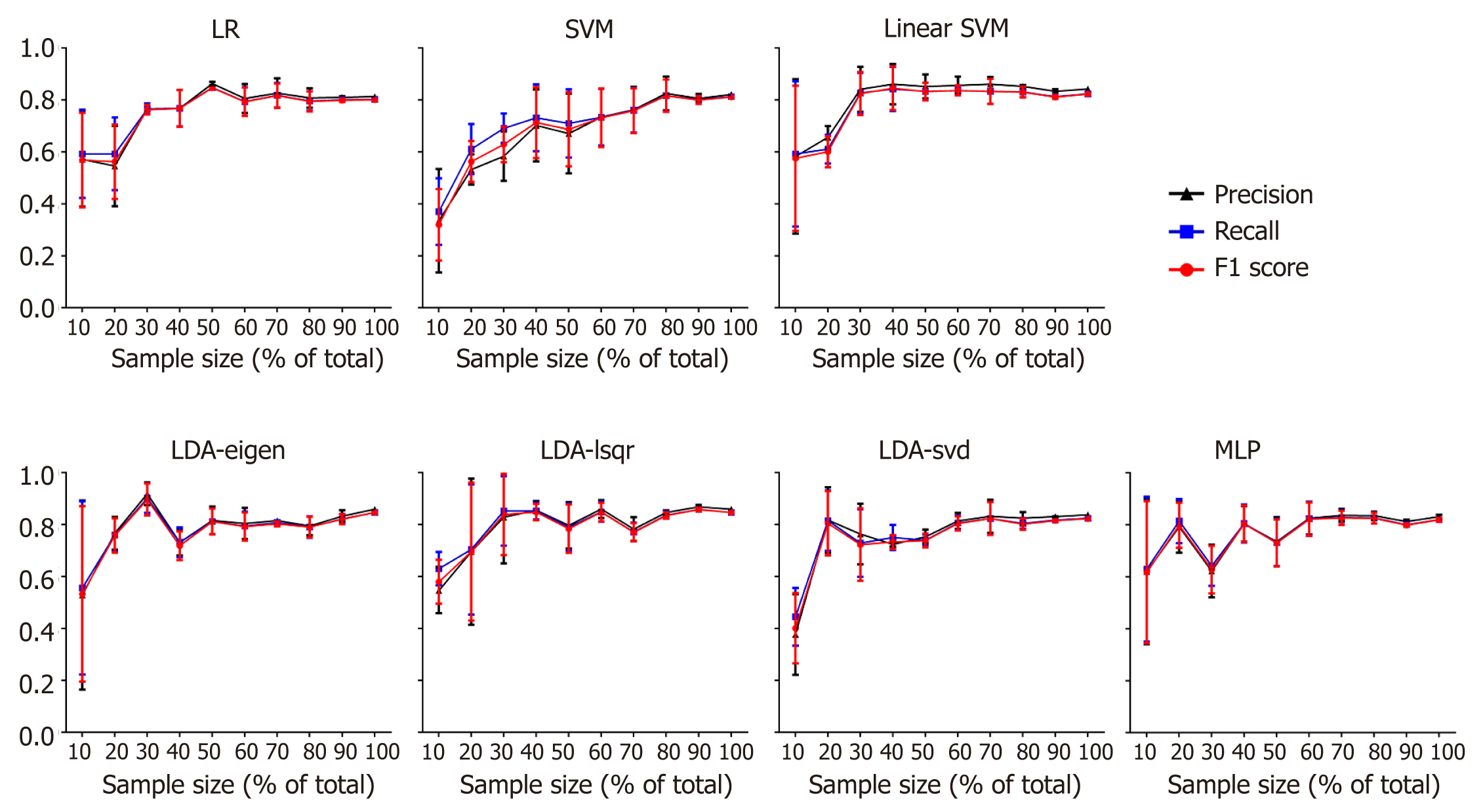
The performance enhanced as the number training samples increased in all the models (except SVM), and the training result leveled off after using 80% of the training data (Figure 4).

Figure 4 F1 score, recall rate and precision rate of different models with increasing sample size. LR: Logistic regression; SVM: Support vector machine; LDA: Linear discriminant analysis MLP: Multilayer perceptron.

All of the models were then analyzed for classification power of different grades. As shown in Table 4, in Linear SVM, LDA – eigen, LDA - lsqr and MLP, models had a higher f1, recall rate and precision rate for G3 and G2 than other models. The f1 score of MLP and Linear SVM was lower than that of LDA – eigen and LDA – lsqr. However, MLP and Linear SVM had a higher recall rate for G3.

Table 4 F1 score, recall rate and precision rate of each grade in different models.

Model	Grade	F1	Recall rate	Precision rate
LR	G1	0.83	0.94	0.75
	G2	0.8	0.73	0.88
	G3	0.73	0.73	0.73
SVM	G1	0.85	0.94	0.77
	G2	0.81	0.75	0.88
	G3	0.73	0.73	0.73
Linear SVM	G1	0.85	0.94	0.77
	G2	0.81	0.73	0.92
	G3	0.8	0.91	0.71
LDA-eigen	G1	0.85	0.94	0.77
	G2	0.85	0.81	0.89
	G3	0.84	0.73	1
LDA-lsqr	G1	0.85	0.94	0.77
	G2	0.85	0.81	0.89
	G3	0.84	0.73	1
LDA-svd	G1	0.85	0.97	0.76
	G2	0.82	0.75	0.9
	G3	0.76	0.73	0.8
LDA-svd	G1	0.85	0.97	0.76
	G2	0.82	0.75	0.9
	G3	0.76	0.73	0.8
MLP	G1	0.83	0.94	0.75
	G2	0.81	0.75	0.88
	G3	0.83	0.94	0.68

LR: Logistic regression; SVM: Support vector machine; LDA: Linear discriminant analysis; MLP: Multilayer perceptron.

Importance of each parameter in different models

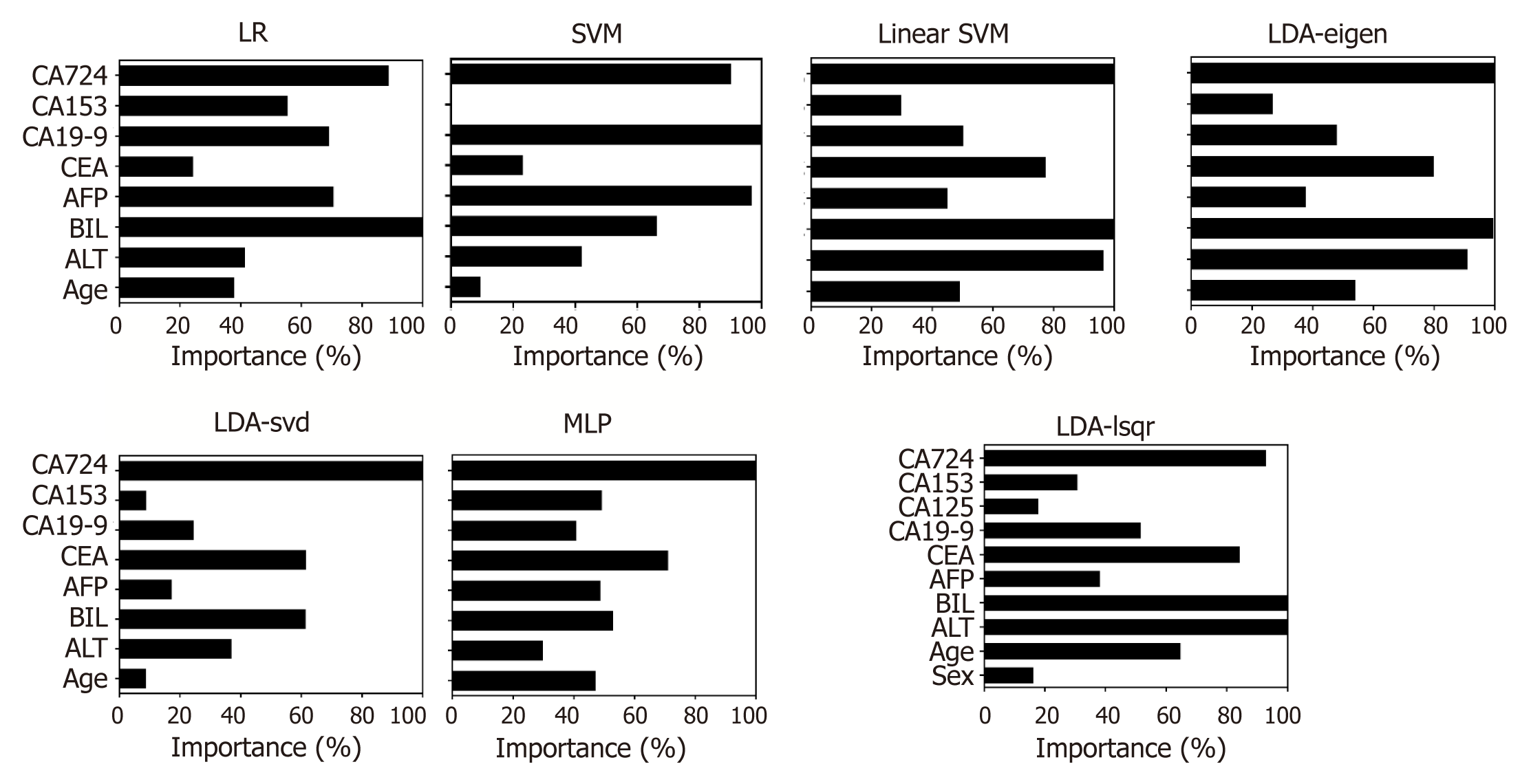
The importance of the clinical parameters when the model performed the best is displayed in Figure 5. It seems that BIL and CA72-4 played important roles in all models, while other variables were important only in specific models, such as CA19-9 for LR and SVM, ALT for Linear SVM, LDA – eigen and LDA - lsqr. Overall, there was a heterogeneous set of the most important predictors in different models (ALT, BIL, CEA, CA19-9 and CA72-4).

Figure 5 The importance of different variables for each model. LR: Logistic regression; SVM: Support vector machine; LDA: Linear discriminant analysis MLP: Multilayer perceptron.

DISSCUSSION

The incidence of PNETs is rapidly increasing[2,3]. Several previous studies demon-strated that the pathological tumor grade of PNETs represents a simple and accurate instrument for predicting mortality risk and disease-free survival, as they accurately reflect the biology and natural history of the cancer. Casadei et al[17] showed that the 5-year disease-free survival rate of G1, G2 and G3 tumors was 78%, 53% and 33%, respectively. In short, the tumor grade of PNETs greatly affects the prognosis and treatment. However, there is still no simple and effective way to non-invasively obtain PNET grades. Therefore, patients will greatly benefit from predicting PNET grades using the outcomes of routine examinations on admission.

In this study, we present results for four classification problems. The clinical data were collected from the outcome of routine examinations on admission, including biochemical and tumor markers, which indicates that the data could be conveniently collected and that data loss would rarely occur. PNET diagnosis and grade were histologically confirmed using tumor tissues obtained from surgical resection to make sure that the pathologic data were objective and precise.

Firstly, the relationship between different clinical parameters and PNET grades were analyzed. We noticed that some studies focused on the natural history and the grade of PNETs. Fitzgerald et al[18] found that the grade of PNETs is related to a patient’s history, including age, gender and tumor size. Our findings are in agreement with these findings. Moreover, our results showed that PNET grade is significantly correlated with outcome of biochemical and tumor markers. Generally, PNETs with a higher tumor grade were associated with higher levels of biochemical and tumor markers. Besides, we found that the difference between G3 and the other two grades was more significant than that between G1 and G2. This result is consistent with previous studies that defined G3 as a “high grade” and G1/2 as a “low grade”[4,19,20].

ML classifiers perform better by using categorical variables compared to continuous variables. In the present study, we used an L way to transform continuous variables into binary variables. Unlike previous studies, we did not use the experimental cutoff value. Instead, we tried to find the cutoff value where the P value was at a minimum in the Chi-square test and the difference between groups was maximum. To make sure the cutoff values were credible, we calculated the cutoff values using our method with 30%-100% of the total available samples. Most of the cutoff values were stabilized when the sample volume was over 80% of the total. The result suggested that our sample size could provide credible cutoff value that contributes to finding the minimum P value in the Chi-square test.

In this study, four supervised classifiers (LR, SVM, LDA and MLP) were used to predict PNET grade. Among these models, SVM and LDA were solved using many algorithms. We trained the models one by one to find the highest f1 score, recall rate and precision rate. Each model was trained by regulating the key parameter values (C for LR and SVM, shrinkage for LDA) in feasible ranges to find the best parameter for each model. The results showed that LDA – eigen and LDA – lsqr performed best and had the highest f1 score. However, in the application of the models, it is more acceptable if a patient with a lower grade tumor is predicted to have a higher grade tumor rather than the other way around. Therefore, we prefer a model that has a higher recall rate for G3. For this purpose, we calculated the precision rate and recall rate score for each grade. The results showed that Linear SVM and MLP had a higher recall rate for G3 (> 90%). However, LDA – eigen and LDA – lsqr had higher f1 scores in total, even though their recall rate for G3 was lower than that of Linear SVM and MLP.

To make sure that the trained models could give stable results and would not be affected by the sample size, we then randomly chose 10% to 100% of the samples in increments of 10%. The f1 score, recall rate and precision rate given by each model with the different sample sizes were calculated. It was found that when the sample size over approximately 50 (60% of total sample volume), the outcome was stabilized in most of the models (except SVM). The result demonstrated that the models trained by the data would give a feasible way to predict the pathological tumor grade of PNETs.

There are still a few limitations in this study. For example, some imaging outcomes that are considered to affect PNET grade, such as tumor size and metastasis found from computed tomography (CT) images[21,22], were not included as parameters. One of the reasons was that in this study, we focused on the objectivity and accessibility of the data. Besides, as a large number of low-grade PNETs were found to be small in size, the tumor size achieved by CT or ultrasound is inaccurate and may cause errors. CT scanning also cannot always detect metastasis[22]. Hence, we plan to use a unified and objective method to judge tumor size and metastasis in further studies. The combination of imaging and serological outcomes may improve the classification power of ML models.

Modern medicine has a formidable track record of applying new technology for identifying and curing disease, prolonging life and improving the quality of life[23]. It has led to a drastic increase in the amount and complexity of patient data. Our study demonstrated the possibility of predictive modeling using traditional data. We used different ML models to predict PNET grades. We found that LDA performed best in overall classification, and Linear SVM obtained the highest recall rate for G3 tumors. The result of our study provides a non-invasive approach to determine the condition of PNETs to offer a reference for treatment.

ARTICLE HIGHLIGHTS

Research background

The incidence of pancreatic neuroendocrine tumors (PNETs) has increased rapidly, and establishment of a prediction system for the tumor grade of PNETs defined by World Health Organization is beneficial for the prognosis and treatment of PNETs. However, determining of the tumor grade by surgery or biopsy means a lot trauma; therefore, a simple and feasible method to non-invasively predict PNET grade would be very meaningful.

Research motivation

Machine learning (ML) algorithms have shown potential in improving the prediction accuracy using comprehensive data. We used four classical ML models in this article and we found that ML could be a potential and feasible method to predict the grade of PNETs by using routine clinical data. ML could be effectively utilized in solving some medical classification problems.

Research objectives

To provide a ML approach to predict PNET tumor grade using clinical data, and ML is effective in classifying PNET grade by using the routine data obtained from the results of biochemical and tumor markers. This approach may be a promising method to non-invasively predict PNET grade and has the potential to be widely used in clinical settings.

Research methods

The biochemical outcomes and tumor markers of 91 patients with histologically confirmed PNETs were collected, and a novel method of minimum P for the Chi-square test (MPCST) was used to divide the continuous variables into binary variables. Four classical supervised ML models, including logistic regression, support vector machine, linear discriminant analysis (LDA) and multi-layer perceptron (MLP) were trained by clinical data. The models were labeled with the pathological tumor grade of each patient. The performance of the different models was then evaluated. Finally, the weight of the different parameters in each of the models were calculated.

Research results

All four models showed a potential performance in this classification task. Among them, LDA showed the best performance in predicting PNET grade, and MLP had the highest recall rate for grade 3 (G3) patients. These results proved that the models trained by the clinical data would provide a feasible approach to predict the pathological tumor grade of PNETs. However, there are still a few limitations in this study. Some parameters like tumor size and metastasis from computed tomography images were not included in this article. Because we think the two parameters may be not objective and may introduce errors in data collection. In general, the result of our study provided a non-invasive method to judge PNET condition and offers a reference for treatment.

Research conclusions

ML is effective in classifying PNET grade by using routine data obtained from the results of biochemical and tumor markers. ML algorithms have shown potential in improving the prediction accuracy of classification of PNET grade using comprehensive data. There is still no effective way to non-invasively determine PNET grade. ML algorithms have shown potential in improving the prediction accuracy using comprehensive data. The combination of imaging and serological outcomes may improve the classification power of ML models. A novel method of minimum P for the MPCST was used to divide the continuous variables into binary variables. Patients of G3 showed more significant differences than grade 1 (G1) and grade 2 (G2). ML is effective in classifying the grade of PNETs by using routine data obtained from the results of biochemical and tumor markers. ML may be a promising method to non-invasively predict PNET grades and has the potential to be widely used in clinical settings.

Research perspectives

Some very simple and routine clinical data may play an important role in medical classification tasks by using ML methods. The combination of imaging and serological outcomes may improve the classification power of ML models. More effective ML models could be utilized in this classification task. The combination of clinical data and experience will help build new ML models.

ACKNOWLEDGEMENTS

We highly acknowledge the contribution by the participating doctors: Yuan-Xing Gao, Zhi-Ming Zhao, Xiang-Long Tan, Ming-Gen Hu, Zi-Zheng Wang, Sai Chou.