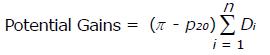Published online Jul 16, 2015. doi: 10.12998/wjcc.v3.i7.625
Peer-review started: August 27, 2014
First decision: October 14, 2015
Revised: April 2, 2015
Accepted: May 16, 2015
Article in press: May 18, 2015
Published online: July 16, 2015
Processing time: 335 Days and 0.6 Hours
Sustained clinical improvement is unlikely without appropriate measuring and reporting techniques. Clinical indicators are tools to help assess whether a standard of care is being met. They are used to evaluate the potential to improve the care provided by healthcare organisations (HCOs). The analysis and reporting of these indicators for the Australian Council on Healthcare Standards have used a methodology which estimates, for each of the 338 clinical indicators, the gains in the system that would result from shifting the mean proportion to the 20th centile. The results are used to provide a relative measure to help prioritise quality improvement activity within clinical areas, rather than simply focus on “poorer performing” HCOs. The method draws attention to clinical areas exhibiting larger between-HCO variation and affecting larger numbers of patients. HCOs report data in six-month periods, resulting in estimated clinical indicator proportions which may be affected by small samples and sampling variation. Failing to address such issues would result in HCOs exhibiting extremely small and large estimated proportions and inflated estimates of the potential gains in the system. This paper describes the 20th centile method of calculating potential gains for the healthcare system by using Bayesian hierarchical models and shrinkage estimators to correct for the effects of sampling variation, and provides an example case in Emergency Medicine as well as example expert commentary from colleges based upon the reports. The application of these Bayesian methods enables all collated data to be used, irrespective of an HCO’s size, and facilitates more realistic estimates of potential system gains.
Core tip: The article’s purpose is to bring attention to the increasing use of Bayesian methods in the clinical field to overcome shortcomings of previous analyses, and provide an application of how such methods are used in clinical management in Australia; in particular, on how to best report and use clinical indicator data for system improvement. The paper identifies flaws associated with traditional clinical indicator reporting techniques which are still often-used; describes part of current Australian clinical indicator reporting methods; and demonstrates how and why Bayesian methods are fundamental to the improved methods overcoming issues that would otherwise arise with such data.
- Citation: Howley PP, Hancock SJ, Gibberd RW, Chuang S, Tuyl FA. Bayesian methods in reporting and managing Australian clinical indicators. World J Clin Cases 2015; 3(7): 625-634
- URL: https://www.wjgnet.com/2307-8960/full/v3/i7/625.htm
- DOI: https://dx.doi.org/10.12998/wjcc.v3.i7.625
Healthcare accreditation systems and quality measurement systems are internationally used for the purposes of improving clinical care and organisational outcomes. Accreditation in healthcare reflects the systematic assessment of hospitals against explicit predetermined standards[1,2] and consists of multiple means of assessment such as self-appraisal, peer-reviewed interviews, scrutiny of documentation, checking of equipment and investigation of key clinical and organisational data[3]. These systems involve considerable levels of resources from the participating agencies and healthcare organizations (HCOs) and are believed to facilitate improved levels of quality in healthcare[4-7].
The Australian Council on Healthcare Standards (ACHS) has a well-established national healthcare accreditation program. It provides robust support for Australian healthcare and is one of the four most commonly cited national healthcare accreditation programs in the world[1,8,9]. In addition to providing a national accreditation scheme, the ACHS supports HCOs by providing sets of clinical indicators (CIs) which HCOs may opt to utilize. HCOs may simply collect their own data, or they may additionally submit their data via the ACHS’s online performance indicator reporting tool for analysis and reporting[9-13]. CIs measure performance in a clinical setting; the reporting of CIs in HCOs aims to detect suboptimal care either in structure, process or outcome, and can be treated as a tool to assess whether a standard in patient care is being met. They may provide evidence for accreditation purposes and guide the process of quality improvement in healthcare[14].
There is world-wide interest in how to integrate clinical indicators within the accreditation process and mechanisms for their collection differ across countries[9]. A comparison of the four most often referenced national accreditation programs internationally[1,8,9] identified the following key points: (1) the Joint Commission (JC) in the United States and Accreditation Canada are examples of accreditation bodies that have integrated the mandatory requirement that hospitals provide core indicators as part of the accreditation process in order to help focus on-site survey evaluation activities in accreditation[9,15-22]. The JC has done so through its ORYX® program and through its integration of measurement data into its Priority Focus Process for the on-site survey[16,17]. Accreditation Canada has done so through its Qmentum program and combining indicator data with their “instrument” data obtained through questionnaires completed by representative samples of clients, staff, leadership and/or other key stakeholders[9,22]; (2) Haute Autorité de Santé, France, has mandatory accreditation for all its hospitals and has connected many of its accreditation standards to indicators. There are 13 criteria that must be satisfied to achieve certification, of which four are linked to indicators. In total, there are 14 indicators connected with accreditation criteria[9,23,24]; and (3) the ACHS, Australia, provides 6-monthly and trend reports to hospitals which have elected to submit their CI data. The contribution of these reports to a hospital’s self-evaluation and quality improvement efforts are relied upon for instigating the CI data collection within hospitals and thus their inclusion in the accreditation process[9].
Taiwan was the fourth country, following the United States, Canada, and Australia, to implement a healthcare accreditation project and the first country in Asia to do so. The reporting of CIs is now required by law for hospitals in Taiwan, and many internal and several nationwide clinical indicator systems have been launched, including three nationwide quality measurement systems: Taiwan Healthcare Indicator Series, Taiwan Clinical Performance Indicators, and Taiwan Community Hospital Association indicators[25]. These three clinical indicator systems are optional for hospitals to utilize. Their target participants are varied and with the diversity of indicators collected there has been difficulty integrating CIs into Taiwan’s accreditation process[26], which is governed by Taiwan’s Joint Commission on Hospital Accreditation. Taiwan’s Ministry of Health and Welfare is currently assessing how best to integrate the CIs from the varied agencies and government departments for enhancing the efficiency and effectiveness of CIs on quality improvement in healthcare.
Since 1993, Australian HCOs preparing for accreditation have submitted data on sets of CIs. The ACHS routinely collates the data in six-month periods and generates reports which are provided to HCOs, along with de-identified reports which are provided to accreditation surveyors, national medical colleges and government bodies. In 2012 the ACHS received data from 670 Australian and New Zealand HCOs on 338 CIs across 22 specialties, or clinical indicator sets[13]. This is the largest source of CI data in the world. The ACHS clinical indicators are not mandatory for any organisation to submit. HCOs select CIs that are relevant to them at that time and where there is a need within that clinical area; for example, high cost procedures, high patient thoroughfare, or a new clinical area to that HCO.
For a given CI, the ith HCO provides the observed number of patients who incur the “event of interest” (Oi) and the number of patients at risk of the event (Di). Traditional methods of analysis and reporting of such data have been flawed, failing to account for sampling variation and focusing on comparing individual HCO proportions with the mean proportion across all HCOs or with an externally set benchmark value determined by experts, with the primary intention of identifying “outliers”. The approach employed in the reporting of the ACHS CIs, as part of the ACHS’s Clinical Indicator Program, shifts the focus towards the potential benefits from system-wide improvements of clinical areas rather than simply comparing individual HCO performances within a clinical area which occurs with other traditional approaches. Further, the new approach has required the application of Bayesian hierarchical models to address issues of small samples, which arise in six-monthly data collection, and to preclude overestimation of the potential system improvements. Accounting for sampling variation through Bayesian hierarchical models additionally reduces HCOs’ concerns of being misrepresented as extreme as a consequence of a small sample size in a given period.
This paper outlines flaws associated with traditional reporting techniques which are still often used elsewhere; describes part of the current ACHS CI reporting methods; provides examples of annual clinical comments and perspectives based on the reports; and demonstrates how and why Bayesian methods have been fundamental to the improved reporting methods overcoming issues that would otherwise arise with such data.
The implementation of league tables which rank CIs within and across HCOs is a common practice which aims to establish an increased level of accountability and competition, and thus provoke individual strategies towards improved performance[27-29]. Deming’s philosophy and systems theory identifies, however, how co-operation rather than competition is required to foster genuine quality improvement and how the system’s components and the interdependencies of these components must be foremost in one’s mind during the improvement cycle[29,30]. The increased focus upon “competition” between HCOs that occurs as a result of publishing league tables can lead to perverse incentives being created[31]. HCOs may, for example, be motivated towards manipulating their data or taking patients that are considered a “low risk” in order to improve their perceived performance, even if this is at the expense of other HCOs in the system[27,31-33].
There is limited, if any, value reporting league tables of HCO performances. Such presentations are likely to mislead[31,32,34,35] even when statistical techniques have been utilised that adjust for differences that arise due to varying sample sizes, as there will inevitably be a top-ranked HCO and bottom-ranked HCO even if all HCOs were providing outstanding service. Whilst confidence intervals are often introduced to determine where statistically significant differences in the ranks exist, the calculation of multiple intervals will increase the risk of identifying differences due to chance. Employing a conservative significance level to compensate will increase the confidence intervals’ widths. In some cases the intervals for HCOs ranked first and last overlap rendering the publication of such tables meaningless[10,32,36,37].
Further, any variations in rank that may be observed with time may be a result of the “regression to the mean” phenomenon[38] rather than reflecting fundamental change in quality. Andersson et al[34] produced a measure of the “…expected change in the rank order if one were to repeat the study” to assess the validity of ranking and demonstrated the “…tremendous uncertainty in the ordering…”[34].
Fundamentally, the league table approach is flawed as it focusses attention on individual HCOs and, in particular, those deemed to be poorer performers requiring improvement rather than addressing issues that may help bring systemic advances to the system of HCOs[27,39]. Thus the analysis of clinical indicators must report more than a simple proportion and rank.
Setting thresholds and performing significance tests using p-values is also commonly practiced, and was previously employed by the ACHS. Comparing individual HCO proportions with a nominal threshold value provides minimal assistance to the HCO system as a whole since most HCOs will be within the tolerance level, potentially reducing motivation to undertake improvement, and HCOs with larger volumes of patients (larger sample sizes) are more likely to yield proportions, or rates, which are statistically significant. Consequently, the principal result of such analyses is the classification of individual HCOs as either satisfactory or not[10,27], rather than highlighting system variation or focusing attention on necessary system-wide improvements.
Focusing upon the system of HCOs helps with identifying clinical areas where investigation and improvement activity may produce the most benefit. An approach was applied that uses the data arising from the system of HCOs to identify a potentially achievable mean proportion and identifies clinical areas with large “potential gains” resulting from achieving such a mean proportion. The ACHS reports achieved this by introducing, for each CI, a measure of the gains (or reduction in the number of undesirable events) that could be achieved if the mean proportion was shifted to the 20th centile. The calculation of these potential gains is based on the amount of variation in the system (represented by the difference in the mean proportion, π, and 20th centile proportion, p20, across all HCOs) and the impact upon the system, or volume effect, (represented by the summed Di, where Di represents the number of patients at risk of the event at the ith HCO, across all n HCOs providing data for the CI) as shown in equation (1).
Math 3
(1)
The estimated potential gains facilitates and motivates scientific investigation within clinical areas by providing a relative measure between CIs of the potential improvement. Smaller variation and smaller potential for system impact [in terms of potential for events occurring, represented by ΣDi in equation (1)] are reflected in a smaller value for the potential gains. Reported as part of the annual Australasian Clinical Indicator reports, this measure enables comparisons of clinical areas for improvement activity rather than allocating responsibility solely to individual HCOs[11].
The use of the 20th centile to calculate potential gains in the system has great appeal as the estimated gains don’t rely upon a subjective target but instead is influenced by the system and the data it has produced; the estimated gains are being guided by the existing between-HCO level of variation in proportions. The 20th centile is approximately one standard deviation from the overall mean proportion and may be considered a practicable goal[10]. Since the distribution of proportions is often not symmetric, using standard errors is less useful.
The potential gains as a measure considers the HCOs as part of an holistic system that may have potential for improvement rather than focusing on individual HCOs’ performances. Such an approach enables healthcare professionals and governing bodies “…to determine those clinical areas where there are potentially greater gains and hence funding for quality improvement activity would be of a higher priority”[10].
In the case of CIs where higher proportions are desired, potential gains are calculated using the 80th centile, p80, as (p80 - π) ΣDi. This represents the number of additional events that would occur if the mean proportion were equal to p80.
The 20th (or 80th) centile and ensuing calculation of the potential gains, however, should not be obtained simply by using the observed proportions (Oi/Di) since they are affected by sampling variation. Further, since the HCOs report their data across six-month periods the observed proportions will be based on large and small sample sizes, affecting the precision and reliability of the estimated proportions[10]. Consider for example an HCO that reports only three individuals at risk of a particular event in a given period. A difference of one in the number incurring the event of interest would correspond in a change in the estimated proportion of 33%. Additionally, it would be more likely that HCOs with such small Di will report the extreme proportions (0% and 100%) despite this most likely not reflecting the true underlying proportion at the HCO.
Rather than exclude HCOs with small data, and thus lose data, a statistical technique known as Bayesian hierarchical modelling and the associated empirical Bayesian shrinkage estimator have been used to better estimate the proportions for the HCOs in a given six-month period. The approach essentially utilizes and combines an individual HCO’s proportion and the summary results from the system of HCOs to produce a better estimate of the individual HCO’s true underlying proportion.
“Medical research applications often involve hierarchical data structures as data are collected on random samples of patients nested within each hospital”[10]. When data are collected from many HCOs there is usually substantial variability among the HCOs in addition to variability within the HCOs due to sampling.
Many readers would be more familiar with the non-Bayesian approach to analyses, known as the frequentist or classical approach, which uses only the information provided by the sample data to make wider inference. In contrast, the Bayesian methodology uses additional prior knowledge or belief, presented in the form of probability distributions, in making wider inference. Bayesian methods essentially assess the appropriateness of the prior knowledge given the new data and quantifies this in the form of probability statements or density functions for the values we are wishing to estimate[40,41]. The “Bayesian methodology has been shown to be particularly useful in both the clinical setting and the area of public health policy when the results of a study must subsequently be used to facilitate a decision”[10]. In the Bayesian paradigm, a two-stage hierarchical model representing the nesting of the patients within HCOs may be used to make inferences[42-48], with the first stage representing the distribution of the HCO-specific proportions (CI proportions among HCOs) and the second stage modelling the additional sampling variation associated with what we observe for the patients within HCOs.
The approach borrows strength from the ensemble[49] of HCOs to estimate any individual HCO’s true proportion better than an individual HCO’s data alone. Essentially the approach uses statistical models for: (1) the conditional probability of the observed counts of events given the unknown true CI proportions (we are attempting to estimate the latter); and (2) a prior distribution for the true CI proportions given their overall mean and variance (the latter may be estimated from the data, in which case the approach is referred to as an empirical Bayes approach). The two statistical models combine via Bayes’ rule[45,50] to produce the probability distribution for the unknown true CI proportions given the observed counts and overall mean and variance; this is known as the posterior distribution.
The expectation of this posterior distribution is the empirical Bayes shrinkage estimator for an HCO’s CI proportion. The estimated proportion for a given HCO is effectively a weighted average of the individual HCO’s observed proportion and the overall mean proportion across all HCOs. The weighting depends upon the systematic variation between HCOs and sample size of the individual HCO, as well as the particular two-stage model’s family of distributions.
To reflect the between-HCO and within-HCO sources of variation in the CI proportions, the ACHS reports use the gamma-Poisson hierarchical model. This model was applied since the gamma distribution could represent the distribution of the ratios of observed to expected numbers of events[10]. Further, using the gamma-Poisson model instead of a beta-binomial model for proportions was shown to result in more conservative estimates of the 20th centile-based potential gains due to a relatively greater shrinkage using the former rather than the latter model[10].
The gamma-Poisson model assumes that the Oi follow a Poisson distribution with mean λiEi, where Ei is the expected number of events at the ith HCO obtained by multiplying Di by the mean proportion, π, and the true ratios of observed and expected numbers of events, λi, are obtained from a gamma distribution with mean, μ, and variance, Sr2. That is, we have Oi ~ Poisson (λiEi) and λi ~ Gamma (μ, Sr2) which combine using Bayes’ rule[45,50] to provide the estimated ratios of an HCO, which are interpretable as proportions by multiplying a ratio by the mean proportion.
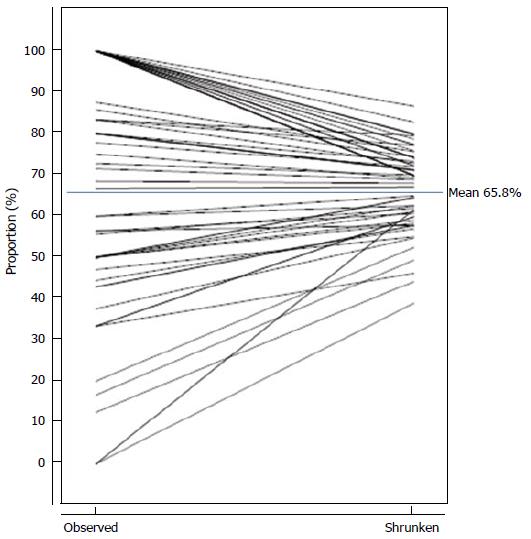
Figure 1 visually demonstrates the changes to the individual HCOs’ estimated proportions and the distribution of proportions following “shrinkage” for a particular clinical indicator having 62 HCO submissions of data; for this indicator a high proportion was desirable. Each HCO returned data enabling the observed proportion (Oi/Di) to be obtained and a shrunken proportion was calculated by the afore-mentioned two-stage models and Bayesian methods and multiplying by π (the overall mean proportion). Figure 1 joins each HCO’s corresponding observed and shrunken proportions. Several HCOs had common observed and shrunken proportions, hence Figure 1 does not show 62 distinct lines.
The Di for the CI ranged from 1 to 78. The observed proportions ranged from 0% to 100%. There were 20 HCO submissions with observed proportions equaling 100%; the Di for these HCOs ranged from 1 to 7. There were 3 HCO submissions with observed proportions equaling 0%; the Di for these HCOs ranged from 1 to 8. The 20th and 80th centiles of the observed proportions were 43.8% and 100% respectively. The 20th and 80th centiles of the shrunken proportions were 58.6% and 74.9% respectively. The mean proportion was 65.8%.
The key points to observe for this example are: (1) HCOs with extreme observed proportions (0% and 100%) are shrunken more greatly towards the mean; a consequence of having smaller Di; (2) not all HCOs having the same observed proportion will have the same shrunken proportion; a consequence of having differing Di; (3) the spread of the distribution of shrunken proportions is far less than the spread of the distribution of observed proportions, reflecting the spread of the true underlying proportions; and (4) the 20th and 80th centiles of the shrunken proportions are closer to the mean proportion than the respective centiles of the observed proportions and hence facilitate better estimates of the potential gains.
The potential gains for a CI are then calculable using the shrunken proportions and 20th or 80th centiles using equation (1), or its equivalent for the 80th centile, and are presented along with other summary information for CIs. Table 1 presents an example of such a report for the clinical area Emergency Medicine.
| CI | Desiredlevel | NumberHCOs | 20thcentile(%) | Meanproportion(%) | 80thcentile(%) | Numerator | Denominator | PotentialGains | StratumGains | OutlierGains |
| 1.1 | High | 309 | 99.2 | 99.1 | 99.9 | 26344 | 26577 | 219 | - | 177 |
| 1.2 | High | 323 | 75.6 | 79.8 | 93.7 | 342984 | 429896 | 59829 | 34972 | 15420 |
| 1.3 | High | 323 | 61.0 | 63.7 | 93.1 | 943806 | 1482555 | 436635 | 164974 | 96017 |
| 1.4 | High | 323 | 64.6 | 69.9 | 96.1 | 1308074 | 1870202 | 488979 | 77692 | 100353 |
| 1.5 | High | 317 | 85.1 | 87.9 | 98.6 | 355355 | 404382 | 43560 | - | 14029 |
| 2.1 | High | 62 | 58.8 | 65.8 | 74.4 | 338 | 514 | 44 | 29 | - |
| 3.1 | Low | 102 | 9.9 | 28.3 | 47.3 | 199881 | 706869 | 129557 | 94225 | 53779 |
| 3.2 | Low | 39 | 30.1 | 60.6 | 82.0 | 6451 | 10639 | 3246 | 861 | 1119 |
| 3.3 | Low | 40 | 19.2 | 48.5 | 70.7 | 7518 | 15502 | 4546 | 2826 | 2032 |
| 4.1 | Low | 7 | 0.0 | 0.1 | 0.2 | 938 | 6742 | 646 | - | 241 |
| 4.2 | Low | 6 | 0.0 | 0.1 | 0.1 | 261 | 5024 | 259 | - | 119 |
| 5.1 | Low | 2 | 23.9 | 23.9 | 23.9 | 358 | 15 | - | - | - |
| 5.2 | Low | 3 | 54.5 | 54.5 | 54.5 | 61 | 112 | - | - | - |
| 6.1 | High | 7 | 66.4 | 71.5 | 92.7 | 10276 | 14363 | 3033 | - | 1143 |
| 6.2 | High | 4 | 20.0 | 37.0 | 46.0 | 2783 | 7519 | 678 | - | 290 |
| 7.1 | High | 10 | 26.4 | 44.4 | 91.8 | 3395 | 7653 | 3630 | - | 1509 |
| 7.2 | High | 7 | 21.9 | 51.4 | 84.8 | 183 | 356 | 119 | - | 38 |
| 7.3 | High | 5 | 21.9 | 17.7 | 33.9 | 854 | 4818 | 778 | - | - |
| 7.4 | High | 4 | 40.8 | 83.6 | 99.8 | 244 | 292 | 48 | - | 33 |
| 8.1 | Low | 28 | 0.9 | 4.1 | 8.8 | 1547 | 37888 | 1203 | 600 | 606 |
| 8.2 | Low | 53 | 1.7 | 4.9 | 6.9 | 49389 | 1008385 | 31885 | - | 10066 |
The potential gains provided in Table 1 provide a measure to help prioritise investigation and improvement activity. Consider CIs 1.2 and 2.1; each are desired to have a high proportion. CI 1.2 has a mean proportion of 79.8% whilst 2.1 has a mean proportion of 65.8%. On this alone, it may seem 2.1 should be the priority for improvement; however, the potential gains incorporates the variation between HCOs as well as the size of the potential impact upon the system represented by “Denominator” which is the total number at risk of an event across all HCOs. When this information is considered we observe potential gains for 1.2 that is some 1360 times the potential gains for 2.1, reprioritising where investigation and improvement activity may be best undertaken.
In addition to the 20th centile-based potential gains, the ACHS reports present estimates of stratum gains and outlier gains, as shown in Table 1. Stratum gains represent the gains that would be achieved from moving the mean proportions of the poorer performing strata to the mean proportion of the best performing stratum. The strata for the HCOs are: public or private; metropolitan or non-metropolitan; and State (region of Australia).
Outlier gains present the gains that may be achieved from improving the outlier HCO proportions to equal the overall mean proportion. Outlier HCOs have differences in observed and expected numbers of events exceeding three times the standard error of the difference, after shrinkage. A funnel plot, as shown in Figure 2, plots for a given CI the HCOs’ differences in observed and expected counts, or Excess count, ordered by Di. Doing so allows a visual check for any patterns that would suggest a volume effect (a pattern due to Di). In this particular case there were no outliers or an effect due to sample size. Whilst traditional methods may have resulted in little more than the reporting of no outliers, the 20th centile gains and stratum gains presented in the ACHS reports focus attention on potential for improvement in the system.
The annual reports described in this paper are part of a two-tiered reporting system. In addition to these annual reports, HCOs receive individual six-monthly reports which identify the individual HCO’s performance (rate) compared with both the entire system’s rate and themselves based on trend analysis of their six-monthly rates. The latter reports are used by individual HCOs to self-assess whilst the annual report is provided to the relevant Colleges before being published and the Colleges are invited to comment on their set of CIs. In earlier editions of this report the response was less than hoped for, but the annual edition, currently in its 15th year, has more recently received and incorporated clinical comments and perspectives on all results.
Vignettes of the types of comments are provided below[12]. Importantly, Colleges and State Governments are reading reports and thus engaging more with the data.
Example 1: Response from the College of Nursing to the CI representing falls for those aged 65 years or more: “There is no significant change to the data reported in 2013 compared to 2012, despite the fact that the HCO population is aging, with higher numbers of complex and higher acuity patients–particularly within the public HCOs….HCOs with outlier rates within this CI need to review their falls management protocols and falls prevention education, to reduce the current rate of falls–which is nearly double the fitted rate for all reporting HCOs”[12].
Example 2:“The Australian Faculty of Rehabilitation Medicine (AFRM) and the Australasian Rehabilitation Outcomes Centre (AROC) are proud of the continued high standard of compliance with the ACHS CIs by all participating HCOs. The AFRM has included the ACHS CIs in the AROC dataset to encourage HCOs to participate in this important collection and thereby promote continued improvement in these processes and outcomes. The quality of the data collected is of a high standard, with well-established, nationally consistent education programs in situ. On that basis, the AFRM and the AROC are confident about the results reported here. HCOs are encouraged to continue reviewing their CI collections to help inform processes and practices in order to maintain the high rates achieved in previous years”[12].
Example 3: Expert commentary from Royal Australian and New Zealand College of Obstetricians and Gynaecologists (RANZCOG) on outcome of selected primipara: “There has been a small increase in the number of spontaneous vaginal births in the selected primipara (CI 1.1), but it remains at around 45.0%. There are several reasons why the number of spontaneous vaginal births will be expected to continue to lessen: (1) women becoming more risk averse and therefore more often requesting obstetric procedures in order to minimize risk. This applies to all women, but particularly in relation to common issues such as how long to tolerate pregnancy progressing beyond the due date; (2) increasing maternal age; and (3) Reducing maternal parity with the consequential reduced morbidity from caesarean section in subsequent pregnancies.
Stratum differences were demonstrated in relation to private and public HCOs (36.4% vs 50.8% respectively). This is expected as the above factors are more prevalent in the private sector than public sector”[12].
Example 4: Expert commentary from RANZCOG on Intrauterine growth restriction: “The rate of CI 8.1 has been steadily improving, but this appears to have plateaued at around 1.64%. Failure to diagnose intrauterine growth restriction remains the most obvious preventable factor in perinatal mortality at term. It has been rewarding to see this statistic fall over the 5 year period and it could be suggested that introducing this CI is partly responsible for this highly desirable improvement”[12].
Example 5: Expert commentary from the Australian and New Zealand College of Ophthalmologists on Cataract Surgery: “Unplanned overnight admission rates following cataract surgery were lower in 2013 with a reduction in the annual rate (CI 1.3). There are known factors such as older age groups, medical co-morbidities and surgery in the latter part of the day that may be contributing. In 2013, there were eleven outlier submissions from eight different HCOs. The outlier organisations can consider a grading/points system based on case complexity to identify cases that should be done in the morning or by an experienced surgeon”[12].
Example 6: Expert commentary from the Australian College of Midwives: General Comment, “The number of services reporting for each CI indicates the ease or difficulty of recording and reporting data defined and possibly the usefulness of the measure to local monitoring. Comparison of local results with the mean and stratified groups would enable health services and professionals to determine areas for policy, practice and research attention”[12].
The ACHS CIs aim to get refined data, controlling for casemix, e.g., infection control for each of coronary-artery bypass, hip replacement, knee surgery, etc. Since there are 22 specialties (sets of indicators) representing the main Colleges in Australia, and hence some 338 CIs, an individual HCO has to select those sets, or subsets of CIs, that are appropriate to their needs. For example, sets based upon paediatrics, obstetrics, oncology, gynaecology or day only procedures or patients will not be relevant to many HCOs. Even for sets that are relevant some of the CIs within the set may not be collected due to costs of obtaining the data from the medical records, or the CI may not be seen as important to the individual HCO. The non-mandatory nature of the CIs is consistent with the non-punitive and non-invasive nature of the reporting methods described. The data collection and reporting method is designed to assist the healthcare system, not place greater burdens upon the system or HCOs unable to sustain the costs of widespread data collection. Whilst the CIs provide a means for HCOs to more easily provide necessary evidence to warrant accreditation, the afore-mentioned reasons along with nuances that exist within any HCO warrants the optional nature of their use. This further attracts some HCOs towards the ACHS accreditation process and to provide data honestly rather than be forced to provide data and be motivated towards manipulating their data or taking patients that are considered a “low risk” in order to improve their perceived performance, even if this is at the expense of other HCOs in the system[27,31-33].
The simplistic ranking of HCOs does not quantify the gains that could be achieved and has many disadvantages. The reporting of indicators which measure clinical and healthcare processes should quantify the potential gains to encourage action. Estimating the gains across many indicators enables the comparison and identification of areas with greater potential improvement and thus prioritisation of resources for investigation and improvement efforts. The required tools and resources to investigate and address those areas with the greatest gains must then be provided.
Bayesian hierarchical models and empirical Bayes shrinkage estimators borrow strength from the collection of HCOs to estimate any individual HCO’s true proportion better than an individual HCO’s data alone, accounting for sampling variation and addressing issues surrounding small sample sizes[49]. Shrinkage estimators are more beneficial in situations where denominators vary in size and some are small[10,51], as is the case for the CI data.
The shrinkage estimator effectively modifies an individual HCO’s observed proportion by drawing it closer to the prior mean. The amount of modification (shrinkage) is less for those HCOs having larger sample sizes (reflecting the increased information being reported by those individual HCOs reducing the effects of sampling variation) and for systems exhibiting large systematic, or between-HCO, variation (reflecting lower strength of knowledge about the prior mean since the prior variance is large in such cases). Thus HCOs having smaller denominators will have their observed proportions shifted more closely towards the overall mean than HCOs having larger denominators. The implementation of the shrinkage estimators not only provides better estimates for each HCO, in particular those that would otherwise be identified as extreme due to small sample sizes, but additionally enables all HCOs to be included in the reports irrespective of size. Further, the approach is reflecting the reality that there is a level of dependence between the HCOs as they are all part of the one system.
The use of CIs as flags for required investigation towards system improvement is a valuable area of research. The development and application of appropriate statistical methods for analysing and reporting CIs is important and should focus on improving the healthcare system. Estimating the potential gains achievable through investigation and quality improvement that reduces the mean proportion to the 20th centile focusses efforts on system-wide improvements rather than assigning blame and onus on individual HCOs. In combination with the empirical Bayesian shrinkage estimators, the estimated potential gains support practicable reports on CIs for healthcare providers.
CIs are screening tools, so just as positive blood tests or breast cancer screening result in review and further investigation so too positive results from the CI analysis must result in further investigation. There are three types of positive results, namely, large variation between HCOs, large variation between strata and outlier HCOs (large variation from expected). This paper has described the use of the difference between the mean and 20th centile proportions to estimate the impact of between HCO variation and stratum and outlier gains which estimate the impact of between stratum variation and variation from expected for individual HCOs. These gains are reported by the ACHS for all 338 CIs[13]. Bayesian methods play a key role in ensuring such measures are not overestimated.
The presented potential gains quantify reductions, or increases for certain CIs, in the numbers of “events of interest”. Whilst it is possible to attribute monetary costs to each event in order to estimate potential financial changes, the problem remains of comparing the vast range of outcomes such as delays due to intensive care unit (ICU) access block, readmissions and out of hours discharges from ICU, adverse events related to medication errors, wound infections and failure to administer venous thromboembolism prophylaxis. Whilst the measures may be converted to indicate potential costs to the healthcare system doing so would take a restricted view of these measures of quality. Further, there remains the issue of how one may compare losses of life with additional waiting times. The simplest approach involves identifying CIs where significant numbers of patients were not receiving the standard of care implied by the CI as being acceptable; however, this remains an area of ongoing research.
P- Reviewer: Guan YS, Sanabria A S- Editor: Song XX L- Editor: A E- Editor: Wu HL
| 1. | World Health Organization. World Health Organization Quality and Accreditation in Health Care Services: A Global Review, 2003 [accessed 2015 Mar 23].. Available from: http://www.who.int/hrh/documents/en/quality_accreditation.pdf. |
| 2. | The Australian Council on Healthcare Standards website [accessed 2015 Mar 22].. Available from: http://www.achs.org.au/about-us/what-we-do/what-is-accreditation/. |
| 3. | Mainz J. Defining and classifying clinical indicators for quality improvement. Int J Qual Health Care. 2003;15:523-530. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 607] [Cited by in RCA: 654] [Article Influence: 31.1] [Reference Citation Analysis (0)] |
| 4. | Greenfield D, Braithwaite J. Health sector accreditation research: a systematic review. Int J Qual Health Care. 2008;20:172-183. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 303] [Cited by in RCA: 299] [Article Influence: 17.6] [Reference Citation Analysis (0)] |
| 5. | Griffith JR, Knutzen SR, Alexander JA. Structural versus outcomes measures in hospitals: a comparison of Joint Commission and Medicare outcomes scores in hospitals. Qual Manag Health Care. 2002;10:29-38. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 50] [Cited by in RCA: 50] [Article Influence: 2.2] [Reference Citation Analysis (0)] |
| 6. | Scrivens E. Assessing the value of accreditation systems. Eur J Public Health. 1997;7:4-8. [RCA] [DOI] [Full Text] [Cited by in Crossref: 23] [Cited by in RCA: 24] [Article Influence: 0.9] [Reference Citation Analysis (0)] |
| 7. | Shaw CD. Evaluating accreditation. IJQHC. 2003;15:455-56. [RCA] [DOI] [Full Text] [Cited by in Crossref: 53] [Cited by in RCA: 42] [Article Influence: 1.9] [Reference Citation Analysis (0)] |
| 8. | Smits PA, Champagne F, Contandriopoulos D, Sicotte C, Préval J. Conceptualizing performance in accreditation. Int J Qual Health Care. 2008;20:47-52. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 11] [Cited by in RCA: 12] [Article Influence: 0.7] [Reference Citation Analysis (0)] |
| 9. | Chuang S, Howley PP, Hancock S. Using clinical indicators to facilitate quality improvement via the accreditation process: an adaptive study into the control relationship. Int J Qual Health Care. 2013;25:277-283. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 8] [Cited by in RCA: 8] [Article Influence: 0.7] [Reference Citation Analysis (0)] |
| 10. | Howley PP, Gibberd R. Using hierarchical models to analyse clinical indicators: a comparison of the gamma-Poisson and beta-binomial models. Int J Qual Health Care. 2003;15:319-329. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 19] [Cited by in RCA: 21] [Article Influence: 1.0] [Reference Citation Analysis (0)] |
| 11. | Howley PP, Chuang SW; Systems theory and improving healthcare, ASEARC: Proceedings of the Fourth Annual ASEARC Research Conference, Sydney, NSW, 2011. . |
| 12. | Low L, O’Connor L, Yen D, Walker S, Lawson T, Bates T, Cadwallender G, Nathan M, Collpy B, Kingsley E. Australasian Clinical Indicator Report: 2006–2013, 15th Edition, 2014, Australian Council on Healthcare Standards, Sydney, Australia. Available from: http://www.achs.org.au/publications-resources/australasian-clinical-indicator-report/. |
| 13. | Low L, Leigh L, O’Connor L, Lord D, Baker J, McIntosh A, Cadwallender G, Bichel Findlay J, Gibberd R, Nathan M. Australasian Clinical Indicator Report: 2005–2012, 14th ed, 2013 ([accessed 2015 Mar 24] Australian Council on Healthcare Standards, Sydney, Australia).. Available from: http://www.achs.org.au/media/75524/ach071_clinical_indicators_web.pdf. |
| 14. | de Vos M, Graafmans W, Kooistra M, Meijboom B, Van Der Voort P, Westert G. Using quality indicators to improve hospital care: a review of the literature. Int J Qual Health Care. 2009;21:119-129. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 132] [Cited by in RCA: 137] [Article Influence: 8.6] [Reference Citation Analysis (0)] |
| 15. | The Joint Commission, Facts about hospital accreditation [accessed 2011 Jun 26].. Available from: http://www.jointcommission.org/assets/1/18/Hospital_Accreditation_1_31_11.pdf. |
| 16. | The Joint Commission, Survey Activity Guide for Health Care Organization. The Joint Commisson, 2011 [accessed 2011 Jun 26].. Available from: http://www.jointcommission.org/assets/1/18/2011_SAG.pdf. |
| 17. | The Joint Commission, Facts about ORYX® for Hospitals (National Hospital Quality Measures) [accessed 2011 Jun 26].. Available from: http://www.jointcommission.org/assets/1/18/ORYX_for_Hospitals_1_25_11.pdf. |
| 18. | The Joint Commission, 2009 ORYX performance measure reporting requirements for hospitals and guidelines for measure Selections [accessed 2011 Jun 24].. Available from: http://www.jointcommission.org/NR/rdonlyres/64C5EDF0-253A-42CE-9DE5-C8AFE6755267/0/09_Oryx_hap.pdf. |
| 19. | Chassin MR, Loeb JM, Schmaltz SP, Wachter RM. Accountability measures--using measurement to promote quality improvement. N Engl J Med. 2010;363:683-688. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 350] [Cited by in RCA: 340] [Article Influence: 22.7] [Reference Citation Analysis (0)] |
| 20. | Accreditation Canada, EDUCATION 2011, Quality Improvement and Indicators [accessed 2011 Jun 24]. Available from: http://www.accreditation.ca/uploadedFiles/Education-Brochure-EN.pdf. |
| 21. | Acceditation Canada, Qmentum [accessed 2011 Jun 24]. Available from: http://www.accreditation.ca/accrediation-programs/qmentum. |
| 22. | Nicklin W. Acceditation Canada’s Qmentum Program: Continuing to Promote Quality Improvement – One Year after Implementation, International society for quality in health care, 26th International Conference, 2009, Oct 13-16 [accessed 2011 Jun 24].. Available from: http://www.isqua.org/Uploads/Conference/Abstracts/Microsoft_PowerPoint_-_B4_Wendy_Nicklin.pdf. |
| 23. | Giraud-Roufast A, Chabot JM. Medical acceptance of quality assurance in health care: the French experience. JAMA. 2008;300:2663-2665. [PubMed] |
| 24. | Haute Autorité de Santé, Certification manual for healthcare organizations, V2010, Haute Autorité de Santé, 2008, France [accessed 2011 Jun 22].. Available from: http://www.has-sante.fr/portail/upload/docs/application/pdf/2010-10/annual-report-2009-summary_2010-10-06_09-13-7_551.pdf. |
| 25. | Chiu WT, Yang CM, Lin HW, Chu TB. Development and implementation of a nationwide health care quality indicator system in Taiwan. Int J Qual Health Care. 2007;19:21-28. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 33] [Cited by in RCA: 33] [Article Influence: 1.7] [Reference Citation Analysis (0)] |
| 26. | Chung KP, Yu TH. Challenges and Perspectives of Development in Quality of Care Indicators: What Else Can We Do. Taiwan J Public Health. 2009;28. |
| 27. | Adab P, Rouse AM, Mohammed MA, Marshall T. Performance league tables: the NHS deserves better. BMJ. 2002;324:95-98. [PubMed] |
| 28. | Goldstein H, Spiegelhalter DJ. League tables and their limitations: statistical issues in comparisons of institutional performance. J of the Royal Statistical Society - Series A. 1996;159:385-443. [DOI] [Full Text] |
| 29. | Berwick DM. A primer on leading the improvement of systems. BMJ. 1996;312:619-622. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 467] [Cited by in RCA: 457] [Article Influence: 15.8] [Reference Citation Analysis (0)] |
| 30. | Deming WE. The New Economics. Cambridge, MA: MIT Press 1993; . |
| 31. | Marshall EC, Spiegelhalter DJ. Reliability of league tables of in vitro fertilisation clinics: retrospective analysis of live birth rates. BMJ. 1998;316:1701-1704; discussion 1705. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 109] [Cited by in RCA: 203] [Article Influence: 7.5] [Reference Citation Analysis (0)] |
| 32. | Anderson P. Popularising HCO performance data. BMJ. 1999;318:1772. [RCA] [DOI] [Full Text] [Cited by in Crossref: 2] [Cited by in RCA: 3] [Article Influence: 0.1] [Reference Citation Analysis (0)] |
| 33. | Marshall MN, Shekelle PG, Leatherman S, Brook RH. The public release of performance data: what do we expect to gain A review of the evidence. JAMA. 2000;283:1866-1874. [PubMed] [DOI] [Full Text] |
| 34. | Andersson J, Carling K, Mattson S. Random ranking of Hospitals is unsound. Chance. 1998;11:34-39. |
| 36. | Appleby J, Bell A. Reporting NHS performance: how did the media perform. BMJ. 2000;321:248. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 115] [Cited by in RCA: 118] [Article Influence: 10.7] [Reference Citation Analysis (0)] |
| 37. | Parry GJ, Gould CR, McCabe CJ, Tarnow-Mordi WO. Annual league tables of mortality in neonatal intensive care units: longitudinal study. International Neonatal Network and the Scottish Neonatal Consultants and Nurses Collaborative Study Group. BMJ. 1998;316:1931-1935. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 51] [Cited by in RCA: 63] [Article Influence: 2.3] [Reference Citation Analysis (0)] |
| 38. | Barnett AG, van der Pols JC, Dobson AJ. Regression to the mean: what it is and how to deal with it. Int J Epidemiol. 2005;34:215-220. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1027] [Cited by in RCA: 1189] [Article Influence: 56.6] [Reference Citation Analysis (0)] |
| 39. | Leyland AH, Boddy FA. League tables and acute myocardial infarction. Lancet. 1998;351:555-558. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 57] [Cited by in RCA: 58] [Article Influence: 2.1] [Reference Citation Analysis (0)] |
| 40. | Ashby D, Smith AF. Evidence-based medicine as Bayesian decision-making. Stat Med. 2000;19:3291-3305. [RCA] [PubMed] [DOI] [Full Text] [Cited by in RCA: 1] [Reference Citation Analysis (0)] |
| 41. | Larson HJ; Introduction to Probability Theory and Statistical Inference, Third Edition, New York, John Wiley and Sons, 1982: 561-562. . |
| 42. | Gurrin LC, Kurinczuk JJ, Burton PR. Bayesian statistics in medical research: an intuitive alternative to conventional data analysis. J Eval Clin Pract. 2000;6:193-204. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 43] [Cited by in RCA: 45] [Article Influence: 1.8] [Reference Citation Analysis (0)] |
| 43. | Sutton AJ, Abrams KR. Bayesian methods in meta-analysis and evidence synthesis. Stat Methods Med Res. 2001;10:277-303. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 152] [Cited by in RCA: 124] [Article Influence: 5.2] [Reference Citation Analysis (0)] |
| 44. | Armitage P, Berry G; Statistical Methods in Medical Research, Third Edition, Blackwell Scientific Publications, Oxford, 1994: 73-74. . |
| 45. | Spiegelhalter DJ, Myles JP, Jones DR, Abrams KR. Methods in health service research. An introduction to bayesian methods in health technology assessment. BMJ. 1999;319:508-512. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 206] [Cited by in RCA: 214] [Article Influence: 8.2] [Reference Citation Analysis (0)] |
| 46. | Burton PR. Helping doctors to draw appropriate inferences from the analysis of medical studies. Stat Med. 1994;13:1699-1713. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 33] [Cited by in RCA: 35] [Article Influence: 1.1] [Reference Citation Analysis (0)] |
| 47. | Gelman A, Price PN. All maps of parameter estimates are misleading. Stat Med. 1999;18:3221-3234. [PubMed] |
| 48. | Kass RE, Steffey D. Prior Effective Sample Size in Conditionally Independent Hierarchical Models. Bayesian Anal. 2012;7. [PubMed] [DOI] [Full Text] |
| 49. | Louis TA, Shen W. Innovations in bayes and empirical bayes methods: estimating parameters, populations and ranks. Stat Med. 1999;18:2493-2505. [RCA] [PubMed] [DOI] [Full Text] [Cited by in RCA: 1] [Reference Citation Analysis (0)] |
| 50. | Gelman A, Carlin JB, Stern HS, Dunson DB, Vehtari A, Rubin DB. Bayesian Data Analysis. 3rd ed. Chapman and Hall. Cambridge, MA: MIT Press 2013; 11-12. |
| 51. | Zaslavsky AM. Statistical issues in reporting quality data: small samples and casemix variation. Int J Qual Health Care. 2001;13:481-488. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 63] [Cited by in RCA: 64] [Article Influence: 2.7] [Reference Citation Analysis (0)] |