Published online Sep 27, 2021. doi: 10.4240/wjgs.v13.i9.1039
Peer-review started: January 29, 2021
First decision: May 4, 2021
Revised: May 10, 2021
Accepted: August 4, 2021
Article in press: August 4, 2021
Published online: September 27, 2021
Processing time: 231 Days and 17.1 Hours
Sutures have been used to repair wounds since ancient times. However, the basic suture technique has not significantly changed. In Phase I of our project, we proposed a “double diabolo” suture design, using a theoretical physical study to show that this suture receives 50% less tension than conventional sutures, and so a correspondingly greater force must be applied to break it.
To determine whether these theoretical levels of resistance were met by the new type of suture.
An observational study was performed to compare three types of sutures, using a device that exerted force on the suture until the breaking point was reached. The tension produced by this traction was measured. The following variables were considered: Tearing stress on entry/exit points, edge separation stress, and suture break stress. The study sample consisted of 30 sutures with simple interrupted stitches (Group 1), 30 with continuous stitches (Group 2), and 30 with the “double diabolo” design (Group 3).
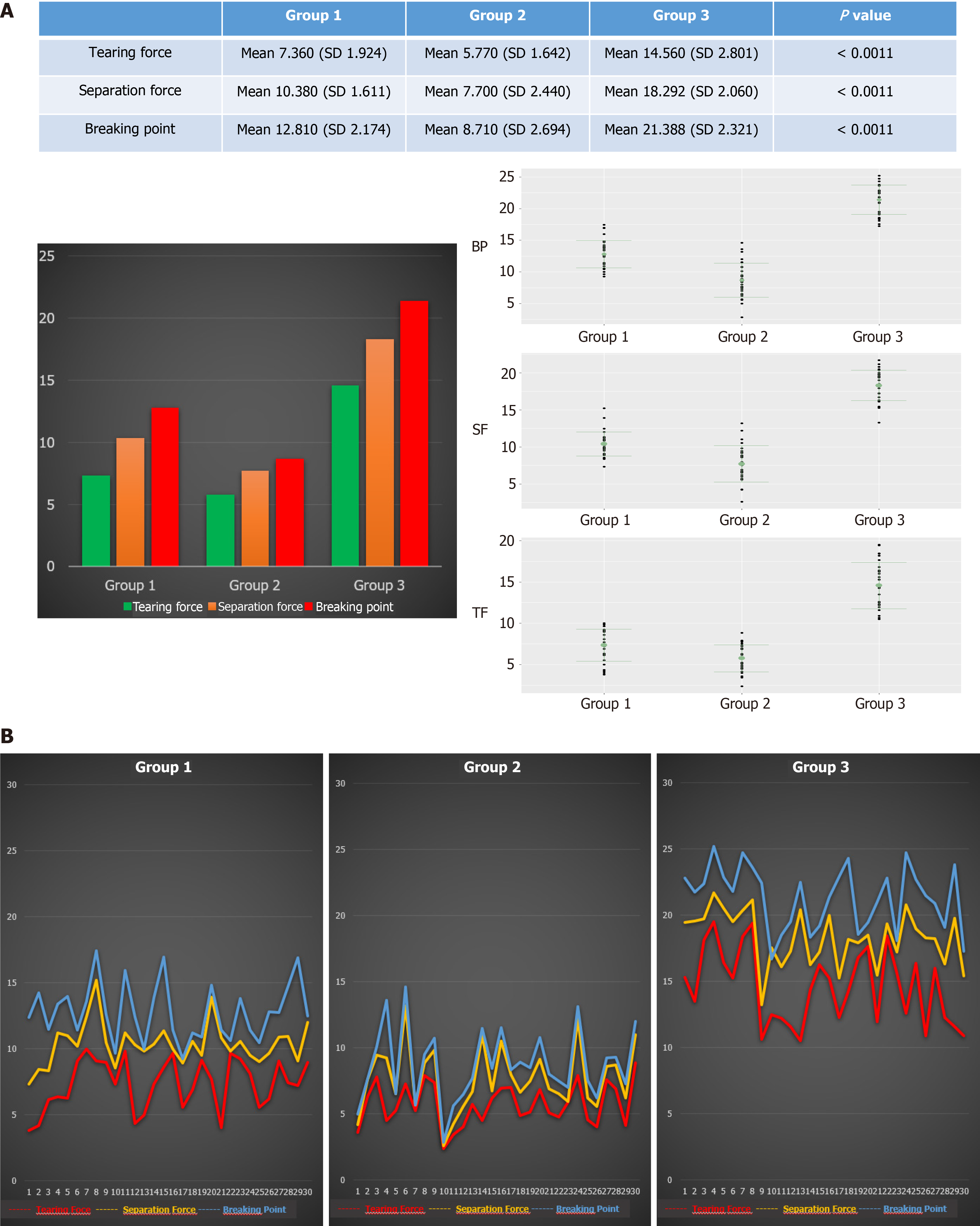
The mean degree of force required to reach the breaking point for each of these variables (tearing, separation, and final breaking) was highest in Group 3 (14.56, 18.28, and 21.39 kg), followed by Group 1 (7.36, 10.38, and 12.81 kg) and Group 2 (5.77, 7.7, and 8.71 kg). These differences were statistically significant (P < 0.001) in all cases.
The experimental results show that with the “double diabolo” suture, compared with conventional sutures, greater force must be applied to reach the breaking point (almost twice as much as in the simple interrupted suture and more than double that required for the continuous suture). If these results are confirmed in Phase III (the clinical phase) of our study, we believe the double diabolo technique should be adopted as the standard approach, especially when the suture must withstand significant tension (e.g., laparotomy closure, thoracotomy closure, diaphragm suture, or hernial orifice closure).
Core Tip: The aim of this project was to design and validate a new technique that imposes the least possible tension on the suture threads and entry/exit points, thus creating a suture that is more stable and resistant. We manufactured a device to apply a progressively increasing separation force to the suture surfaces, and to measure the tension exerted until the breaking point is reached. With this device we compared three groups: Simple interrupted stitches, continuous stitches, and our proposed technique.
- Citation: Pérez Lara FJ, Zubizarreta Jimenez R, Moya Donoso FJ, Hernández Gonzalez JM, Prieto-Puga Arjona T, Marín Moya R, Pitarch Martinez M. Novel suturing technique, based on physical principles, achieves a breaking point double that obtained by conventional techniques . World J Gastrointest Surg 2021; 13(9): 1039-1049
- URL: https://www.wjgnet.com/1948-9366/full/v13/i9/1039.htm
- DOI: https://dx.doi.org/10.4240/wjgs.v13.i9.1039
Sutures are a vital element of almost all surgical procedures. They join tissues, close and stabilise wound margins, and promote healing[1]. The desirable characteristics of sutures are well documented, and include aspects such as high and predictable tensile strength, ease of application, and secure knotting[2].
On a daily basis, surgeons must draw wound tissues closer together and maintain this state, but their choice of suture design is often empirical, based on experience alone. To date, no methodical investigation has been conducted to determine the ideal suture design from the perspective of theoretical physics.
Needles were first used between 50000 and 30000 BCE, and from 20000 BCE until the Renaissance, bone needles were the best available. It is reasonable to assume that these needles were also used to stitch wounds[3]. Throughout history, materials such as linen, cotton, horsehair, animal tendons and intestines, and precious metal filaments have been used to draw wound edges together and to act as ligatures. Preferences and technologies have evolved over time, resulting in the highly sophisticated products used in current practice. Nevertheless, despite these advances[4-7], little progress has been made in suturing, and most surgeons continue to use the two classical techni
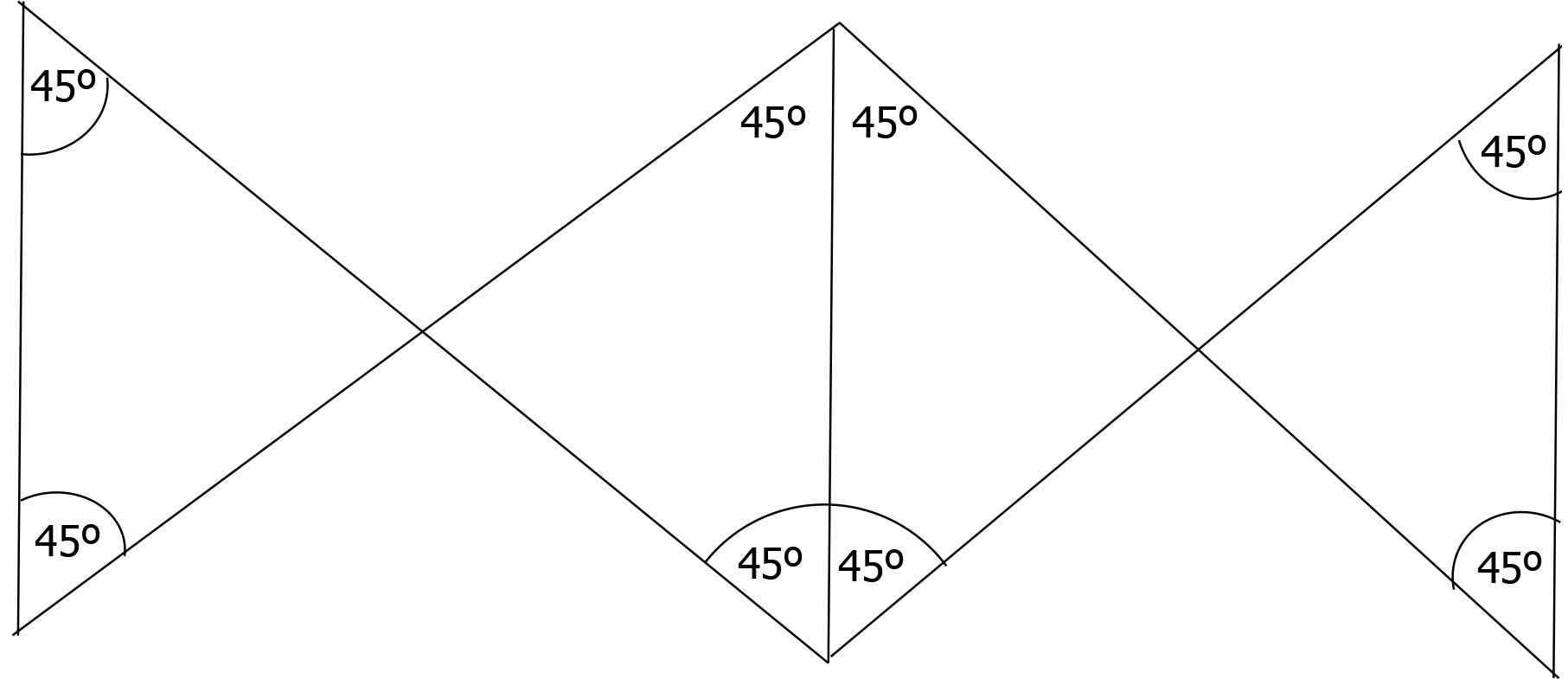
The aim of this project was to design and validate a new technique that imposes the least possible tension on the suture threads and entry/exit points, thus creating a suture that is more stable and resistant. By examining the vector forces exerted on a suture, it can be seen that distribution of the tension on a thread that joins two diverging points will decrease according to the cosine of the angle between the thread and the perpendicular of the force applied to separate the points. In other words, the wider the angle of approach of the thread, the less tension it must support. For example, if the angle in question is expanded to 45º, the cosine will be 0.7; therefore, the tension on the thread is equal to 0.7 of the force exerted, that is, it is reduced by 30%. In this project, our initial consideration is that the sutures currently in use, whether interrupted or continuous, join the points in a straight line. Therefore, the angulation is zero and the sutures are subjected to maximum tension.
On the basis of this physical law, and as a proposal for an improved suture design, we recently published (in Phase 1 of our study[8]) details of the double diabolo suture, in which the suture point is supported by two central inverted double angles and by four lateral angles, thus creating eight 45º angles (Figure 1) and more widely distributing the stress exerted. In the earlier study, we showed theoretically that the tension on the thread was reduced by 65% compared to the interrupted suture and by 50% compared to the continuous suture. Moreover, the tension on the entry/exit points was reduced by 33% and 50%, respectively.
However, these theoretical physical postulates must be confirmed experimentally, showing that with the suture design that we describe, both the suture thread and the entry/exit points are indeed subjected to less tension (for a given separation force applied) than is the case with conventional sutures, and therefore that a greater force can be applied to our sutures before they break.
In this second phase of this project, an observational study was conducted to compare the two types of suture used in standard practice, the simple interrupted suture (Group 1) and the continuous suture (Group 2), with the proposed new design, the double diabolo (Group 3). To compare these three groups, we manufactured a device (Figure 2) to apply a progressively increasing separation force to the suture surfaces, and to measure the tension exerted until the breaking point is reached. These tests were performed on 90 sutures, 30 for each group, and the results obtained were compared.
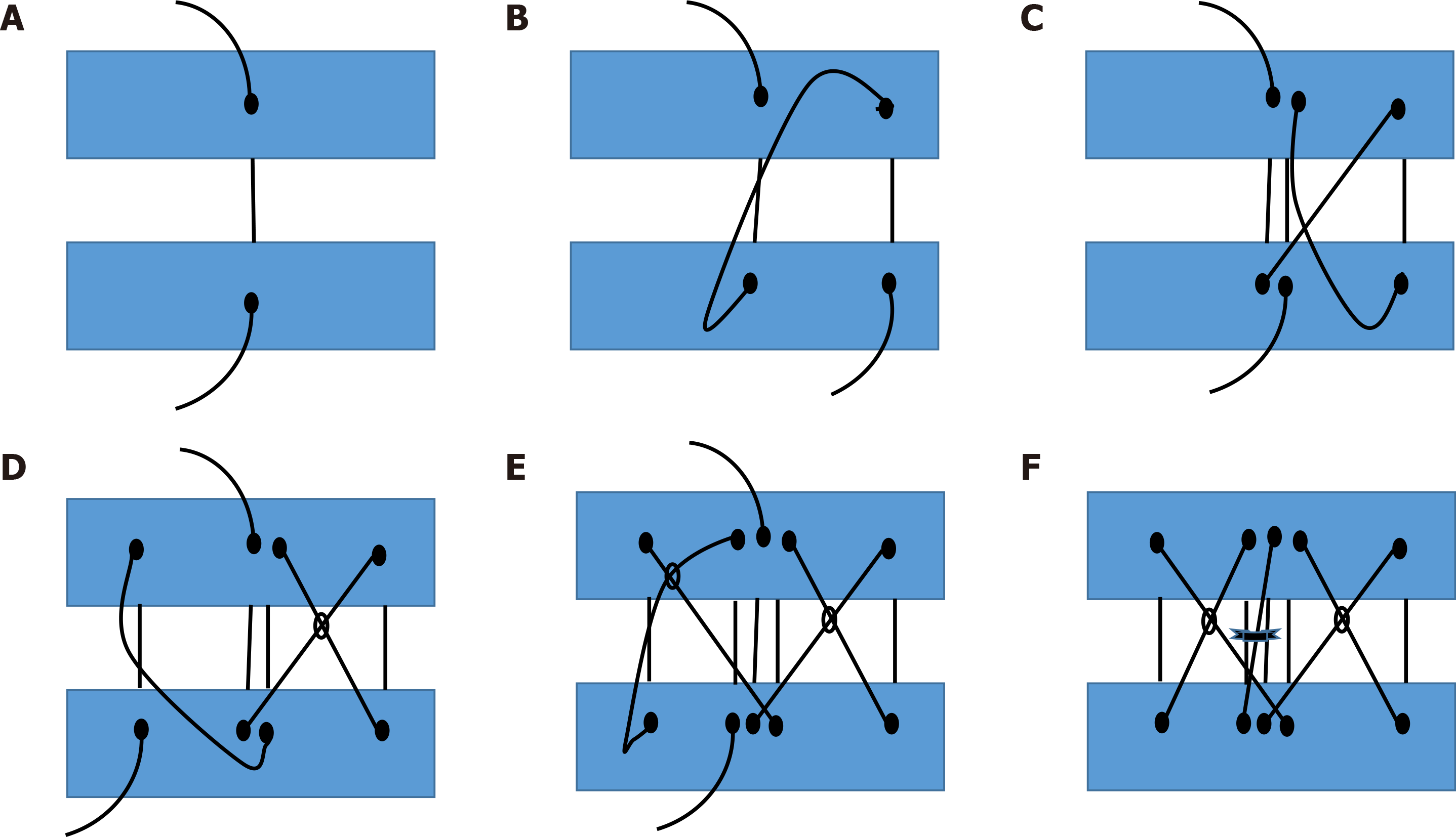
Sutures were inserted perpendicular to the two surfaces to be joined, and each suture was knotted in the centre.
The whole suture was created with a single thread via ligatures perpendicular to the two surfaces to be joined, knotting only the first and last points.
With this suture, each stitch was addressed by eight 45º angles. We started with a central stitch that was perpendicular to the surfaces to be joined (Figure 3A). Then we created an X-shaped stitch to the right (Figure 3B), returned with a second central stitch (Figure 3C), created another X-shaped stitch, this time to the left (Figure 3D), and finally returned with a third central stitch to complete the “central column” (Figure 3E). The stitch assembly was then knotted with the thread that was centrally located at the outset (Figure 3F).
Measuring the force exerted: The measuring device (Figure 2) was composed of a base to which a metal frame was fitted, with a dynamometer and two plates attached to a screw mechanism (like a small garrotte), applied to two fragments of sutured material. With this device, the tension exerted on the suture can be progressively increased until it breaks. The amount of force exerted was measured with the dynamometer.
In testing the three suture designs, three moments were taken as points of reference: First, when the entry/exit points began to tear (tearing force, TF); Second, when the edges of the sutured material began to separate (separation force, SF); and Third, when complete separation of the sutured elements occurred, either because of the thread breaks or due to complete rupture of the sutured material (breaking point, BP). The tension exerted at each moment was measured and compared for the three types of suture.
In order to avoid bias in our results, the same parameters were applied to each of the three groups. Thus, in every case the same material was used (PVC sheets, 6 cm long and 2 mm thick). In every case, three stitches were formed, at 1 cm from the edge, with the same separation between them. The thread used was always the same (monofilament gauge 0) and all knots were tied six times, and cut at 1 cm from the knot. The statistical study is shown in Table 1.
| Aim | To compare the force exerted at which the breaking point is reached, for the three types of suture (Groups 1, 2 and 3) according to the measurements of tearing (TF), separation (SF) and rupture (BP) |
| Method | The study sample was composed of 90 elements |
| Clinical variables | (1) Tearing (the force applied at which the suture points begin to tear); (2) Separation (the force applied at which the suture edges begin to separate); and (3) Break (the force applied at which the suture breaks) |
| Classification of the variables (suture type) | (1) Group 1 (simple interrupted suture); (2) Group 2 (continuous suture); and (3) Group 3 (double diabolo suture) |
A descriptive analysis was performed of the sample (90 elements). Summary statistics (mean, standard deviation, median, minimum and maximum) were calculated for each of the clinical variables. The Kolmogorov-Smirnov test of normality was performed to determine the most suitable means of comparing the suture types. This test considered the following hypotheses:
\ (H_0 = \text{The sample follows a normal distribution}\)
\ (H_1 = \text{The sample does not follow a normal distribution}\)
Therefore, if P < 0.05, the hypothesis that the sample had been drawn from a population with a normal distribution was rejected. The comparative analysis based on the suture-type classificatory variable was performed by analysis of variance when the variables followed a normal distribution and otherwise by the non-parametric Kruskal-Wallis test. The following hypotheses were considered:
\(H_0= \text{Groups 1, 2 and 3 react to exerted pressure in the same way}\)
\(H_1= \text{At least one of the groups reacts differently }\)
Therefore, if P < 0.05, the hypothesis that Groups 1, 2 and 3 react in the same way to the pressure exerted was rejected. In both of these evaluations, if intergroup differences were detected, two-by-two tests were performed, using the Bonferroni correction. The Student's t-test was used in the parametric case and the Mann-Whitney U test in the non-parametric case. In both cases, when P < 0.05, the hypothesis that the groups were equal was rejected.
The 90 cases considered were divided equally among the three types of suture. For each case, the above-described device was used to apply a separation force to the two surfaces of the suture, and the resulting measurements were obtained for the study variables. The summary statistics (mean, standard deviation, median, minimum and maximum) obtained for the variables TF, SF, and BP are detailed in Table 2. For the overall sample of 90 sutures, the average TF of the entry/exit points was 9.23 ± 4.41 kg, the average SF of the suture edges was 12.12 ± 4.96 kg, and the average BP was 14.3 ± 5.82 kg. The variables TF, SF, and BP were not normally distributed, producing statistics of D = 0.12, 0.16 and 0.10 and P values of < 0.01, < 0.01 and < 0.05 respec
| mean ± SD | Median | Min | Max | |
| TF | 9.23 ± 4.41 | 7.9 | 2.4 | 19.5 |
| SF | 12.12 ± 4.96 | 10.7 | 2.6 | 21.7 |
| BP | 14.3 ± 5.82 | 12.98 | 2.85 | 25.2 |
The results of the comparative analysis are detailed in Figure 4. In brief, the mean values for TF, SF, and BP were highest in Group 3 (14.56, 18.28, and 21.39 kg), followed by Group 1 (7.36, 10.38, and 12.81 kg) and Group 2 (5.77, 7.7, and 8.71 kg). The differences among the three groups were statistically significant (P < 0.001). A two-by-two test was carried out to determine whether the pairs of suture types presented differences, showing that in every case (TF, SF, and BP), the differences between Groups 1 and 3, Groups 2 and 3, and Groups 1 and 2 were statistically significant (P < 0.005).
Inserting sutures is one of the most challenging and time-consuming surgical tasks[9]. The limitations associated with the work of a human operator, together with the repetitive nature of this operation make it a suitable candidate for automation.
The purpose of sutures in general is to approximate wound tissues, without excess tension, minimising ischaemia and tissue injury. As the wound heals, the strength of the scar increases until the tissue approaches or regains its original tensile strength. For either single- or multi-layer wound closure, the suture size or diameter chosen should be the smallest for purpose, thus minimising both the tissue trauma with each needle pass and the amount of foreign material inserted. However, smaller-diameter sutures are associated with lower tensile strength, and so a balance must be struck between the size of the suture and the need to maintain the tissue approximation[2].
Since ancient times, mankind has used materials in one way or another to bond the edges of wounds and promote healing. However, despite much progress in the development of new suture materials and efforts to enhance techniques, little significant improvement has been achieved for decades[10,11] and indeed, concerns the distribution of stress angles for millennia.
On the other hand, numerous proposals have been made to improve the stability of the suture. Thus, Sen et al[12] proposed an algorithm to minimise the length of the suture and to maintain the needle at an orthogonal angle to the tissue entry point. Another study by Wieskötter et al[13] compared different types of suture and the biomechanical stability provided to the tendons in each case.
Israelsson et al[14-17] addressed the question of which technique should best be used to achieve continuous closure, and in accordance with their experimental and clinical data recommended the short stitch technique.
On the other hand, a meta-analysis by Henriksen et al[18] found no significant differences between the results obtained by the interrupted and the continuous suture techniques. This meta-analysis concluded that the best evidence was obtained for laparotomy incision closure by means of the “small bites” technique with a 2-0 slowly absorbable suture in which aponeurosis was only present in a suture: Wound length ratio of at least 4:1. Kubota et al[19] studied the mechanical properties of six types of circumferential sutures for the tendon, and reported that the suture termed "Lin-locking" supported the greatest tensile force. However, to the best of our knowledge, no high-quality evidence has been reported on the best suture material or technique to reduce, for example, the rate of incisional hernia after a laparotomy closure.
As Albert Einstein said, "The important thing is not to stop questioning," and this notion has been applied by Srivastava et al[20] and by Srivastava et al[21]. These authors highlight the fundamental importance of physical laws in the field of surgery, noting that the basic mechanisms by which living and non-living beings function are guided by the laws of the pure sciences, that is, physics, chemistry, and mathematics. In this respect, Srivastava et al[21] performed a systematic search in Medline (1960–2008) using keywords such as mechanics, Laplace's Law, Pascal's Law, the laws of vectors and suture techniques, etc. and discussed, among other topics, the laws of mechanics, thermodynamics and the vectors applied to soft tissue and bone and Laplace's Law, with respect to colon perforation, compression therapy, childbirth, ruptured varicose veins, herniated discs, etc. Moreover, consideration of Pascal's Law is necessary when conducting hernia repair and the Heimlich manoeuvre. The components of the forces derived from trigonometry, which come into play when a suture is inserted, reveal how the wound may be closed. The thickness and the bite of the suture determine the extent of the tissue reaction, and the tension exerted may be reduced, according to the cosine of the angle. However, to date no suture design taking advantage of this physical law has been proposed.
Thus, our review of the literature did not reveal any prior in-depth study of the physical laws that govern the tensions generated in sutures, conducted in order to create a new, more effective suture design. The real-world situation continues unchanged, and so the use of continuous sutures and simple interrupted stitches (with minor variations) remains standard practice, with stitches perpendicular to the traction forces and therefore without achieving any reduction in the tension exerted on the thread.
Sutures, therefore, continue to fail, either due to the thread breaking or to tissue tearing, in both cases due to their inability to withstand the tension exerted. For this reason, and in view of our finding, after evaluating the physical formulations of many possible suture structures, that the greater the angle of the thread path with respect to the direction of the force exerted on it, the less tension will need to be withstood, we have designed a new type of suture. The design we propose obtained the best results in the theoretical model, and features four 45º angles on each part of the surfaces to be joined (forming eight angles in all), which rest upon a triple-column central structure.
The relatively poor performance of continuous sutures was highlighted both in our theoretical study and under experimental conditions. It is important to note that the tension generated in continuous sutures includes a lateral force at each entry/exit point which is equivalent to the force on the cosine of the angle, and that this force can provoke lateral tears, destabilising the suture even when relatively little force is applied. In the design we propose, however, although the lateral angles are also subjected to tension, the vertical force applied is only half that received by the continuous suture. Because it is multiplied by the cosine of the angle, the resulting lateral force on each entry/exit point is only half that exerted on the continuous suture. Therefore, the new suture design is twice as resistant to lateral tearing.
As observed in our earlier study on this question, the weakest version of the new suture design was that obtained when the central stitches were passed through the same entry/exit point, in which case the tension exerted was much greater. This variable was considered in our preliminary tests, which showed that even this weaker version of the new design withstood 30% more force than the continuous suture or the simple interrupted suture methods before reaching the breaking point.
Finally, we considered a suture design with separate central points. This reduced the tension on each of the entry/exit points, which meant that the suture was almost three times stronger than continuous sutures and almost twice as strong as the interrupted suture method.
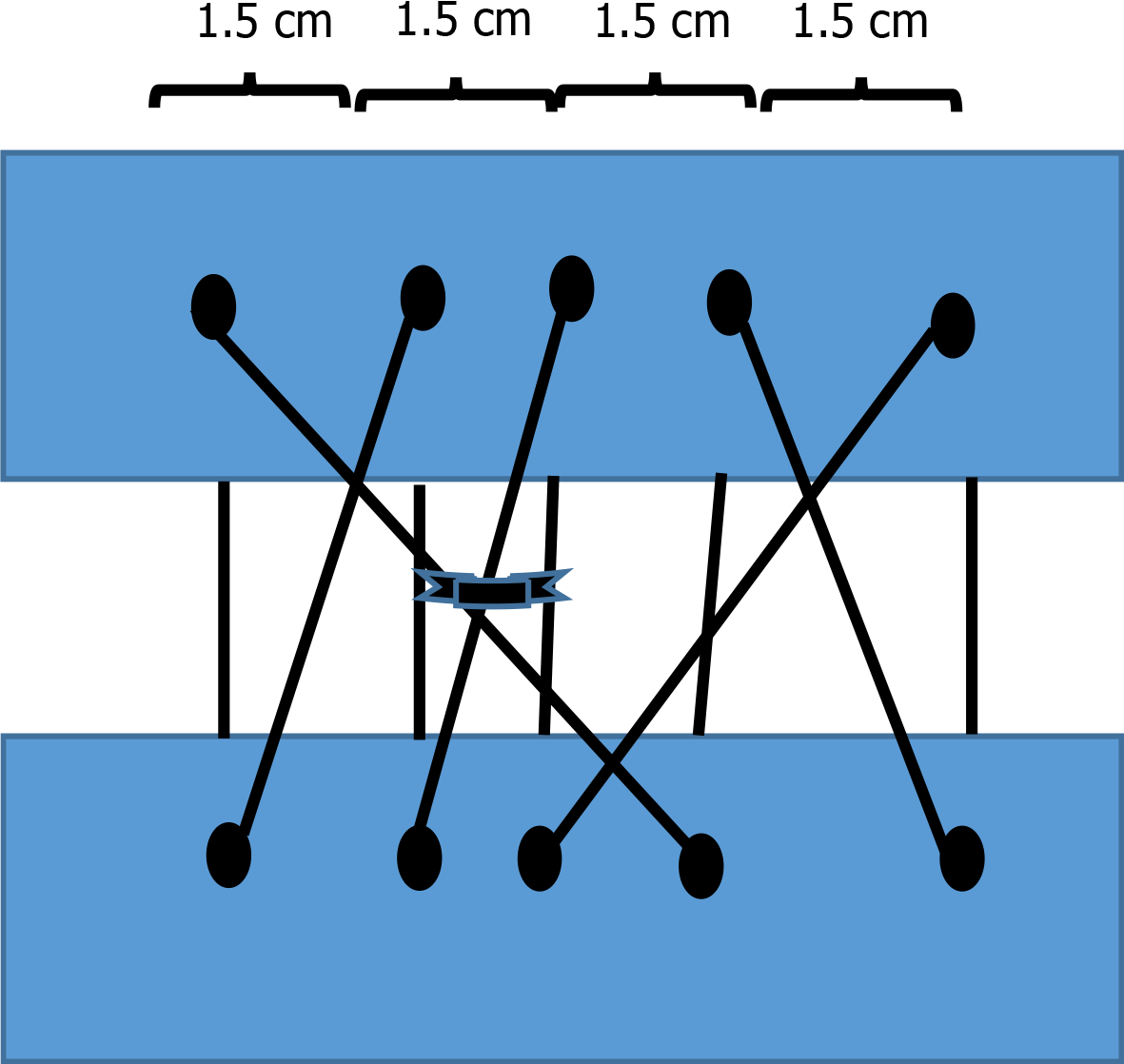
In view of these considerations, and for maximum suture stability, for Phase 3 of our project (the clinical study) these central points will be sited approximately 1-1.5 cm apart, producing the suture model shown in Figure 5. It is also interesting to note that with this design each point of the double-diabolo suture can unite 6 cm of tissue, which makes it very useful in practical terms; for example, a 24 cm laparotomy could be closed with just four sutures, making the procedure much less laborious and time consuming.
In this context of clinical application, it is also important to note that the surgical closure of laparotomies is associated with a failure rate of approximately 15% and a corresponding occurrence of incisional hernias[4,14,22]. This incidence of incisional hernias has remained constant over the last decade despite numerous technical and material modifications[23]. While the early failure of laparotomy closure and the development of an evisceration is almost always attributed to technical errors, the development of an incisional hernia is assumed to be of multifactorial origin[24,25].
Deerenberg et al[26] reported that the annual cost of incisional hernia repair in the United States was $3.2 billion. Therefore, if the results of our work are confirmed in the clinical study (Phase 3) and if the breaking point of our suture is proven to be almost twice that of conventional sutures, it would be possible to reduce the incidence of laparotomic hernias by half, producing an annual financial saving, in the United States alone, of $1.6 billion.
In summary, the results obtained in this study experimentally confirm our hypothesis that the double diabolo suture design results in less tension being exerted on the thread and on the entry/exit points (for a given separation force) than is the case with conventional sutures. In consequence, the double diabolo design has a breaking point that is almost twice that of the simple interrupted suture and more than twice that of the continuous suture. As observed above, in vivo results have still to be obtained. For this purpose, Phase III of our study is now in progress, in which we will evaluate the results of laparotomy closure comparing the performance of the double diabolo suture with that of the two traditional techniques. We believe that if the theoretical and experimental findings are reproduced in the clinical phase, the technique we describe should enter into standard practice, especially in cases in which the suture must withstand significant tension, as is the case for example with laparotomy closure, thoracotomy closure, diaphragm suture and the closure of a hernial orifice.
The basic suture technique has not changed significantly since ancient times.
To find a suture more resistant than the usual ones.
To compare the two types of suture used in standard practice with the proposed new design, the double diabolo.
The authors manufactured a device to apply a progressively-increasing separation force to the suture surfaces, and to measure the tension exerted until the breaking point is reached.
With the “double diabolo” suture, in comparison with conventional sutures, greater force must be applied to reach the breaking point.
The results obtained in this study experimentally confirm our hypothesis that the double diabolo design has a breaking point that is almost twice that of the simple interrupted suture and more than twice that of the continuous suture.
Phase III of our study is now in progress, in which we will evaluate the results of laparotomy closure comparing the performance of the double diabolo suture with that of the two traditional techniques.
Manuscript source: Invited manuscript
Specialty type: Surgery
Country/Territory of origin: Spain
Peer-review report’s scientific quality classification
Grade A (Excellent): 0
Grade B (Very good): 0
Grade C (Good): C
Grade D (Fair): 0
Grade E (Poor): 0
P-Reviewer: Kelemen D S-Editor: Ma YJ L-Editor: Filipodia P-Editor: Li JH
| 1. | Matalon S, Kozlovsky A, Kfir A, Levartovsky S, Mazor Y, Slutzky H. The effect of commonly used sutures on inflammation inducing pathogens - an in vitro study. J Craniomaxillofac Surg. 2013;41:593-597. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 12] [Cited by in RCA: 8] [Article Influence: 0.7] [Reference Citation Analysis (0)] |
| 2. | Ethicon Wound Closure Manual. Somerville, NJ: Johnson & Johnson. February 2, 2019. Available from: https://www.ethicon.com/. |
| 3. | Kirkup J. The Evolution of Surgical Instruments: An Illustrated History from Ancient Time to the Twentieth Century. Publisher: Novato, Calif.: Historyofscience.com. 2006: 449-465. Available from: https://librarysearch.ohsu.edu/permalink/f/t8l2fp/CP71132283300001451. |
| 4. | Högström H, Haglund U, Zederfeldt B. Suture technique and early breaking strength of intestinal anastomoses and laparotomy wounds. Acta Chir Scand. 1985;151:441-443. [PubMed] |
| 5. | Högström H, Haglund U, Zederfeldt B. Tension leads to increased neutrophil accumulation and decreased laparotomy wound strength. Surgery. 1990;107:215-219. [PubMed] |
| 6. | Israelsson LA. The surgeon as a risk factor for complications of midline incisions. Eur J Surg. 1998;164:353-359. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 55] [Cited by in RCA: 44] [Article Influence: 1.6] [Reference Citation Analysis (0)] |
| 7. | Trimbos JB, van Rooij J. Amount of suture material needed for continuous or interrupted wound closure: an experimental study. Eur J Surg. 1993;159:141-143. [PubMed] |
| 8. | Pérez Lara FJ, Zubizarreta Jimenez R, Hernández González JM, Prieto-Puga T, Moya Donoso F. A novel suturing technique, based on physical principles. World J Adv Res Rev. 2020;08:080-090. [RCA] [DOI] [Full Text] [Cited by in Crossref: 1] [Cited by in RCA: 1] [Article Influence: 0.2] [Reference Citation Analysis (0)] |
| 9. | Fretz P, Fischer R. Possible phycomycetes granuloma in the larynx of a horse. Can Vet J. 1976;17:293-297. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 111] [Cited by in RCA: 94] [Article Influence: 3.5] [Reference Citation Analysis (0)] |
| 10. | Bloemen A, van Dooren P, Huizinga BF, Hoofwijk AG. Randomized clinical trial comparing polypropylene or polydioxanone for midline abdominal wall closure. Br J Surg. 2011;98:633-639. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 57] [Cited by in RCA: 62] [Article Influence: 4.4] [Reference Citation Analysis (0)] |
| 11. | Fink C, Baumann P, Wente MN, Knebel P, Bruckner T, Ulrich A, Werner J, Büchler MW, Diener MK. Incisional hernia rate 3 years after midline laparotomy. Br J Surg. 2014;101:51-54. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 187] [Cited by in RCA: 214] [Article Influence: 17.8] [Reference Citation Analysis (0)] |
| 12. | Sen S, Garg A, Gealy D, McKinley S, Jen Y, Goldberg K. Automating multi-throw multilateral surgical suturing with a mechanical needle guide and sequential convex optim.ization. In IEEE International Conference on Robotics and Automation (ICRA), 2016. Available from: https://goldberg.berkeley.edu/pubs/icra2016-final-suturing.pdf. |
| 13. | Wieskötter B, Herbort M, Langer M, Raschke MJ, Wähnert D. The impact of different peripheral suture techniques on the biomechanical stability in flexor tendon repair. Arch Orthop Trauma Surg. 2018;138:139-145. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 23] [Cited by in RCA: 25] [Article Influence: 3.6] [Reference Citation Analysis (0)] |
| 14. | Israelsson LA, Jonsson T. Overweight and healing of midline incisions: the importance of suture technique. Eur J Surg. 1997;163:175-180. [PubMed] |
| 15. | Israelsson LA, Jonsson T. Suture length to wound length ratio and healing of midline laparotomy incisions. Br J Surg. 1993;80:1284-1286. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 132] [Cited by in RCA: 119] [Article Influence: 3.7] [Reference Citation Analysis (0)] |
| 16. | Millbourn D, Cengiz Y, Israelsson LA. Effect of stitch length on wound complications after closure of midline incisions: a randomized controlled trial. Arch Surg. 2009;144:1056-1059. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 233] [Cited by in RCA: 232] [Article Influence: 15.5] [Reference Citation Analysis (0)] |
| 17. | Cengiz Y, Blomquist P, Israelsson LA. Small tissue bites and wound strength: an experimental study. Arch Surg. 2001;136:272-275. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 67] [Cited by in RCA: 64] [Article Influence: 2.7] [Reference Citation Analysis (0)] |
| 18. | Henriksen NA, Deerenberg EB, Venclauskas L, Fortelny RH, Miserez M, Muysoms FE. Meta-analysis on Materials and Techniques for Laparotomy Closure: The MATCH Review. World J Surg. 2018;42:1666-1678. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 39] [Cited by in RCA: 53] [Article Influence: 7.6] [Reference Citation Analysis (0)] |
| 19. | Kubota H, Aoki M, Pruitt DL, Manske PR. Mechanical properties of various circumferential tendon suture techniques. J Hand Surg Br. 1996;21:474-480. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 96] [Cited by in RCA: 88] [Article Influence: 3.0] [Reference Citation Analysis (0)] |
| 20. | Srivastava A, Sood A, Joy SP, Woodcock J. Principles of physics in surgery: the laws of flow dynamics physics for surgeons - Part 1. Indian J Surg. 2009;71:182-187. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 14] [Cited by in RCA: 18] [Article Influence: 1.1] [Reference Citation Analysis (0)] |
| 21. | Srivastava A, Sood A, Joy PS, Mandal S, Panwar R, Ravichandran S, Sarangi S, Woodcock J. Principles of physics in surgery: the laws of mechanics and vectors physics for surgeons-part 2. Indian J Surg. 2010;72:355-361. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 28] [Cited by in RCA: 25] [Article Influence: 1.7] [Reference Citation Analysis (0)] |
| 22. | Schumpelick V, Kingsnorth AN. Closure of laparotomy. In: Schumpelick V, Kingsnorth AN, (eds). Incisional Hernia. Part V. Berlin, Springer, 1999: 231-234. |
| 23. | Israelsson LA, Jonsson T. Closure of midline laparotomy incisions with polydioxanone and nylon: the importance of suture technique. Br J Surg. 1994;81:1606-1608. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 67] [Cited by in RCA: 54] [Article Influence: 1.7] [Reference Citation Analysis (0)] |
| 24. | Wadström J, Gerdin B. Closure of the abdominal wall; how and why? Acta Chir Scand. 1990;156:75-82. [PubMed] |
| 25. | Petersen S, Ludwig K. Comments on the publication of Korenkov M, Paul A, Sauerland S, Neugebauer E, Arndt M, Chevrel JP, Corcione F, Fingerhut A, Flament JB, Kux M, Matzinger A, Myrvold HE, Rath AM, Simmermacher RKJ (2001) Classification and surgical treatment of incisional hernia. Langenbeck's Arch Surg 386:65-73. Langenbecks Arch Surg. 2001;386:309. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 3] [Cited by in RCA: 10] [Article Influence: 0.4] [Reference Citation Analysis (0)] |
| 26. | Deerenberg EB, Harlaar JJ, Steyerberg EW, Lont HE, van Doorn HC, Heisterkamp J, Wijnhoven BP, Schouten WR, Cense HA, Stockmann HB, Berends FJ, Dijkhuizen FPH, Dwarkasing RS, Jairam AP, van Ramshorst GH, Kleinrensink GJ, Jeekel J, Lange JF. Small bites vs large bites for closure of abdominal midline incisions (STITCH): a double-blind, multicentre, randomised controlled trial. Lancet. 2015;386:1254-1260. [PubMed] |