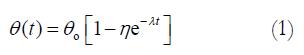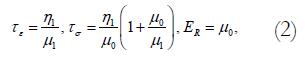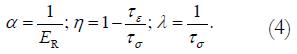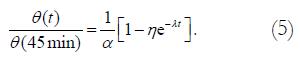Time-dependent viscoelastic properties along rat small intestine

Abstract

AIM: To measure the time-dependent (viscoelastic) behavior in the change of the small intestinal opening angle and to test how well the behavior could be described by the Kelvin model for a standard linear solid.

METHODS: Segments from the duodenum, jejunum, and ileum were harvested from 10 female Wistar rats and the luminal diameter, wall thickness, and opening angle over time (θ(t)) were measured from rings cut from these segments.

RESULTS: Morphometric variations were found along the small intestine with an increase in luminal area and a decrease in wall thickness from the duodenum to the ileum. The opening angle obtained after 60 min was highest in the duodenum (220.8±12.9°) and decreased along the length of the intestine to 143.9±8.9° in the jejunum and 151.4±9.4° in the ileum. The change of opening angle as a function of time, fitted well to the Kelvin model using the equation θ(t)/θo = [1-ηexp (-λt)] after the ring was cut. The computed creep rate λ did not differ between the segments. Compared to constant calculated from pig aorta and coronary artery, it showed that α agreed well (within 5%), η was three times larger than that for vascular tissue, and λ ranged ±40% from the value of the pig coronary artery and was a third of the value of pig aorta.

CONCLUSION: The change of opening angle over time for all the small intestine segments fits well to the standard linear spring-dashpot model. This viscoelastic constant of the rat small intestine is fairly homogenous along its length. The data obtained from this study add to a base set of biomechanical data on the small intestine and provide a reference state for comparison to other tissues, diseased intestinal tissue or intestinal tissue exposed to drugs or chemicals.

Key Words: Biomechanics, Standard linear solid, Creep, Opening angle

INTRODUCTION

The small intestine, like other hollow organs such as heart, blood vessels, bladder and urethra, is functionally subjected to dimensional changes depending on active and passive biomechanical properties. Hence, the biomechanical properties of the small intestine are of particular functional importance.

Most of the data relating to the mechanical aspects of the gastrointestinal (GI) tract deal with motility patterns, flow rates, peristaltic reflexes, and tone in sphincter regions[1-7]. Data in the literature pertaining to the passive mechanical properties of small intestine are concerned with the length-tension relationship in circular and longitudinal tissue strips in vitro[8-11], the compliance[12], and the stress-strain relationship of the intact wall[13,14]. These studies have provided valuable information on some mechanical properties of small intestinal tissue and the distensibility of the intact intestinal wall. However, we still lack a complete database of mechanical parameters to fulfill detailed biomechanical analysis of small intestinal physiology.

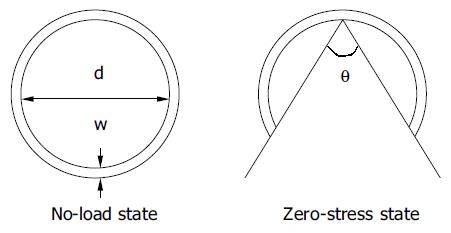
In biomechanical analysis, it is important to determine the stress-free state as the reference for the strain analysis. Residual stress and strain are the internal stress and strain that reside in the organ when external forces are removed (the no-load state). Residual strain has been demonstrated in the small intestine[15-18]. Residual stress reduces transmural stress and strain variations at physiological loads in biological tissues and hence may optimize the mechanical function. The opening angle is commonly used to characterize residual stresses in hollow organs, such as the cardiovascular system and the GI tract. When a hollow organ is cut into rings perpendicular to the central axis, and the rings are then cut radially, the rings will open over a period of time into sectors. When the opening angle has reached a final, static angle, the tissue is considered to have attained a “zero-stress state”. Since zero-stress configuration serves as the reference state for computing stress and strain under physiological or pathophysiological conditions, knowing it is essential in any mechanical analysis. It was reported that the opening angle of rat small intestine reached steady state opening angles after 30-60 min[15-18].

Viscoelastic properties have been described for the normal and diseased human rectum using pressure data[19,20]. The viscoelastic behavior of the intestinal wall during diabetes has been investigated by Zhao et al[21]. However, information is lacking in the time-dependent course of the opening angle. The gradual increase of opening angle over time, until reaching steady sate is defined as creep and reflects the viscoelastic properties of the organ wall. The aims of the current study were: (1) to provide the data on the morphometry of the small intestine in rats, (2) to study the time-dependent changes of the opening angle (creep) along the length of the intestine and (3) to model this relationship based on the assumption that the small intestine behaves like a standard linear solid and derives viscoelastic constants to allow for comparison with other tissue types in the literature.

MATERIALS AND METHODS

Sample preparation

Ten female Wistar rats weighing 220-240 g were included in this study. The rats were anesthetized with pentobarbital sodium (50 mg/kg ip). Following laparotomy, the calcium antagonist, papaverine (60 mg/kg) was injected into the lower thoracic aorta through an iv cannula (22 G/25 mm), in order to abolish contractile activity in the GI tract. Once muscular relaxation was achieved, three 6 cm long segments were harvested from the duodenum, jejunum and ileum. The duodenum was taken from the descending part starting 1 cm from the pylorus, the jejunum from 5 cm distal to the ligament of Treitz, and the ileum from 5 cm proximal to the ileo-cecal valve. The residual contents in the lumens were gently cleared using saline and the segments were then placed immediately into cold Krebs solution containing 6% dextran and 10^-2 moL MgCl and aerated with a gas mixture (95% O₂ and 50 mL/L CO₂, pH 7.4) for 30 min.

From the proximal end of each segment, rings of 1-2 mm in length were cut for the morphometric measurement and zero-stress state experiment. Each ring was placed into a separate Petri dish filled with cold Krebs solution as mentioned above. The rings were placed into the dishes with a portion of the ring running between two metal pins planted into the surface of the dish in order to assist in keeping the rings upright after opening. Three successive rings from each of the three intestinal segments were arranged in series and the rings were cut radially opposite to the mesentery (at 90° relative to the horizontal plane) with a pair of microsurgery scissors, while in the solution. Successive rings were cut open, each after 5 min. Each series of rings was filmed using a video camera (SONY CCD Camera, Japan) and a videocassette recorder for later analysis.

Data analysis

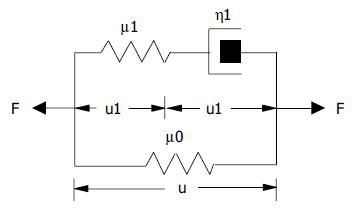
The morphometric data were obtained from digitized images captured from videocassette at 10, 20, 30, 40, 50 s, 1, 2, 3, 4, 10 min, and every 5 min afterwards until 60 min after the initial cut (Optimas 5.2 image capture software, Optimas Corp., USA). Measurements of inner diameter (d), wall thickness (w), and opening angle (θ) were made using dedicated software (Sigmascan 4.1, Jandel Scientific). The opening angle θ was defined as the angle subtended by two radii drawn from the midpoint of the inner wall to the inner tips of two ends of the specimen (Figure 1). The measured data were used to model the change of opening angle as a function of time, primarily by fitting the observed data to the Kelvin model for a standard linear solid (Figure 2). Thus, the data were fitted to the exponential function[22]

Math 1

Math 1 Math(A1).

Figure 1 Schematic diagram of wall thickness (w), inner diameter (d), and opening angle (q) for a ring radially cut into a sector.

Figure 2 Kelvin body, a mechanical model for a standard linear solid viscoelastic material. m1 and m0 are spring constants; h1 is a coefficient of viscosity; u is the displacement including u1 for dashpot and u1’ for spring; F is the sum of the force.

where θo = asymptotic steady state value of the opening angle, λ =the creep rate (s^-1), t = time after the initial cut (s), η = the creep fraction (nondimensional).

This equation relates to the Kelvin body as follows. In the model, μ₁ and μ₂ are spring constants and η₁ is a coefficient of viscosity. By letting

Math 2

Math 2 Math(A1).

where τe=relaxation time for constant strain, τ_σ = relaxation time for constant stress, E_R = relaxed elastic modulus.

We obtained the equation describing this model:

Math 3

Math 3 Math(A1).

We defined

Math 4

Math 4 Math(A1).

The empirical constants η and λ could then be used to plot predicted creep curves and for comparison with other tissues.

For most rings, the opening angle reached 90% of its maximum value in 45 min. Subsequently, the opening angle data were normalized by the angle at 45 min before fitting the data to the exponential function. In order to take this normalization into account, the equation modeling a standard linear solid was modified as follows. Taking Equation (1) and letting θ (45 min)=αθo, we have

Math 5

Math 5 Math(A1).

The empirical constants α, η, and λ were calculated for the data obtained in this study and are presented in Table 2.

Table 2 Standard linear solid coefficients determined for duodenum, jejunum, and ileum of rat small intestine (mean±SE).

	α	η	λ(s–1)	R2
Duodenum	0.954±0.023	0.710±0.013	1.04×10–3±1.09–04	0.989
Jejunum	0.978±0.017	0.779±0.012	1.29×10–3±1.05–04	0.992
Ileum	1.005±0.013	0.720±0.012	1.63×10–3±1.33–04	0.992

Statistical analysis

The data were representative of a normal distribution and results were subsequently expressed as mean±SE. Analysis of variance (ANOVA) was used to test for the differences in the viscoelastic constants (α, η, and λ ) for the various intestinal segments (Sigmastat 2.0^TM). In case of significance, data were evaluated in pairs by a multiple comparison procedure (Student-Newman-Keuls method). If the normality test or the equal variance test failed, Kruskal-Wallis one-way analysis of variance on ranks was used. P<0.05 was considered statistically significant.

RESULTS

Morphometry data

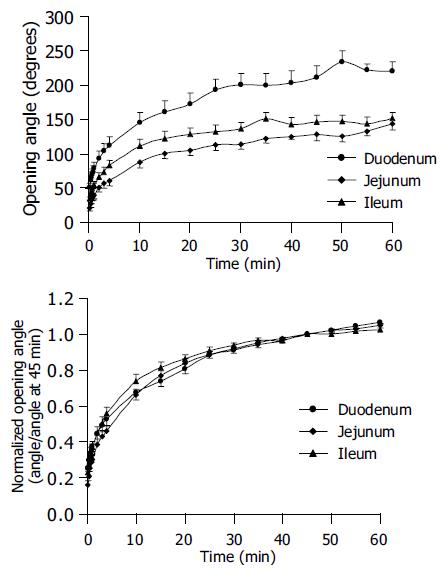
Seventy-eight intestinal rings, and 30 duodenal, 18 jejunal, and 30 ileal rings were obtained from 10 rats. There were fewer jejunal rings because the jejunum was implemented in the study after the fourth rat was completed. This was done in order to obtain a more complete dataset. The highest wall thickness of 0.88±0.03 mm was found in the duodenum. The wall thickness decreased to 0.72±0.06 mm in jejunum and 0.66±0.02 mm in ileum (Table 1, P<0.05). The biggest inner diameter was in the ileal rings and the smallest in the jejunal rings (Table 1, P<0.05). The maximum opening angle was achieved within 60 min, and it was highest in the duodenum (220.8±12.9°) and decreased along the length of small intestine (Table 1, P<0.01).

Table 1 Average opening angle at 45 and 60 min and maximal luminal area and wall thickness for rings cut from rat duodenum, jejunum, and ileum from rat intestine (mean±SE).

	Duodenum	Jejunum	Ileum
Angle (45 min)	211.1±17.2	128.5±10.1b	145.9±9.2b
Angle (60 min)	220.8±12.9	143.9±8.9b	151.4±9.3b
Lumen diameter (mm)	0.86±0.03	0.73±0.04a	0.89±0.03
Wall thickness (mm)	0.88±0.03	0.72±0.06a	0.66±0.02b

^aP<0.05,

^bP<0.01 vs duodenum.

Creep of opening angle

The changes of opening angle and normalized opening angle as function of time (creep) are shown in Figure 3. The opening angles became bigger as function of time. The opening angle was significantly bigger in the duodenal rings than in the other two segmental rings at all time points (Figure 3 top, P<0.01). However, the opening angles did not differ between the jejunal and ileal rings (Figure 3 top, P>0.05). After the opening angle data were normalized by the angle at 45 min, the normalized opening angles as function of time did not differ between the duodenal, jejunal and ileal rings (Figure 3 bottom, P>0.05).

Figure 3 Changes of opening angle and normalized opening angle as function of time.

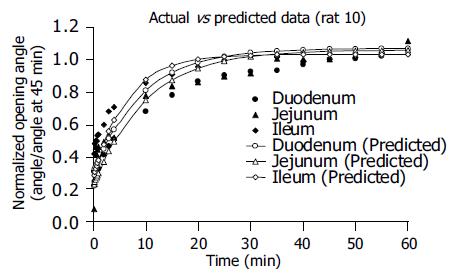
The empirical constants α, η, and λ from a standard linear model analysis did not differ between the different segments (Table 2, P>0.05). Experimental data and predicted data are shown in Figure 4. The solid points represent experimental data of θ(t)/θ(45 min), and the hollow points represent calculated values of θ(t)/θo using the empirical constants α, η, and λ. It showed that the predicted creep curves agreed well with data obtained from this study.

Figure 4 Experimental data and predicted data in rat 10.

DISCUSSION

The time-dependent change of the intestinal opening angle reflects viscoelastic properties (creep). The major finding in this study is that the opening angles at all time points are bigger in the duodenum than in the jejunum and ileum in the normal rats. The change of opening angle for all the small intestine segments showed a slow creep phase and the behavior fitted well to the standard linear spring-dashpot model. The empirical constants α, η, and λ calculated from the standard linear solid model did not differ among the three intestinal segments. Furthermore, we have confirmed previous data that both opening angle and the wall thickness decrease from the duodenum to the ileum, whereas the lumen area increases.

Axial variations of morphometric parameters of small intestine

Our results and previous study[15] has demonstrated substantial axial variations of the morphometric parameters. A decrease in wall thickness is in line with findings in prior studies[24]. Several zero-stress state studies have been done in the GI tract[15-18]. All GI studies done so far showed that the rings open into sectors when cut radially. When radial cuts are made, the duodenal rings are more likely to turn inside out producing large opening angles and therefore indicate a larger residual strain than the jejunal and ileal rings[15]. From a mechanical point of view, a large residual strain may be a natural way of efficiently resisting luminal pressures. Thus, it is likely that the compressed duodenal mucosa may be better protected against injury from pressure changes produced by frequent contractions and the luminal contents ejected at intervals from stomach. In contrast, the less compressed ileal mucosa represents a region under a relatively lower and stable pressure.

Creep of opening angle of intestinal segments

Creep occurs when the material is suddenly stressed and the stress is maintained constant. Hence, the material continues to deform[25]. Creep is a feature of viscoelasticity that is found in most materials including those in the GI tract. Mechanical models, such as the Maxwell model, the Voigt model, and the Kelvin model (also called the standard linear solid)[25,26] are often used to describe the visco-elastic behavior of materials. We assumed that the intestine was a standard linear solid and described the change of opening angles of intestine as function of time using this model. A slow creep phase was found and the behavior fitted well to the standard linear spring-dashpot model. Bharucha et al[27] developed a technique to assess quasi-static colonic P-V curves in the human descending colon and demonstrated that colonic P-V curves approximate to a power exponential function and are reproducible within subjects. In the present study, the experimental data also fit to the exponential function[22]. The predicted creep curves were plotted using the empirical constants α, η, and λ calculated for standard linear solid model. The constants were relatively similar for all three intestinal segments, indicating that the viscoelastic properties of the rat small intestine are fairly homogenous. This is consistent with the relaxation data of normal small intestine reported by Zhao et al[21] (unpublished data). Using these constants, it was also found that θ(t)/θo reached 95% of the full amplitude after 35 min for the duodenum and jejunum and after 30 min for the ileum. The data obtained from this study add to a base set of morphometric and biomechanical data on the small intestine. These data also provide a reference state for comparison to other tissues, diseased intestine or intestine exposed to drugs or chemicals.

Comparison to other studies

The research by Han and Fung[22] on the pig aorta showed that the opening angle reaches 95-98% of the steady-state value after 10-15 min. The constants α, η, and λ obtained in the present study were compared to those calculated from work done by Han and Fung[22] and Frobert et al[23] for pig aorta and coronary artery (Table 3). The results for α agreed very well, η was three times larger than that for vascular tissue and λ ranged ±40% of the value found by Frobert et al[23] for the pig coronary artery and was a third of the value that was found by Han and Fung[22] for the pig aorta. It is likely that the differences are caused by structural differences between tissues[25]. Studies using enzymatic digestion of structural components have been carried out on the zero-stress state analysis of the cardiovascular system[28]. Similar studies may shed more light on the viscoelastic properties of different tissue components in the intestine.

Table 3 Comparison of standard linear solid coefficients obtained in this study and from the literature.

	Rat duodenum	Rat jejunum	Rat ileum	Pig aorta[22]	Pig coronary artery[23]
α	0.954	0.978	1.005	0.981	0.971
η	0.71	0.779	0.72	0.263b	0.274b
λ (s–1)	1.04×10–3	1.29×10–3	1.63×10–3	3.31×10–3b	1.17×10–3

^bP<0.01 vs rat intestine.

In conclusion, the geometric parameters and biomechanical properties of the different segments of small intestine are different. The results obtained from this study add to a base set of morphometric and biomechanical data on the small intestine. The data obtained in this study provide a reference state for future comparison to other tissues, diseased intestinal tissue or intestinal tissue exposed to drugs or chemicals.