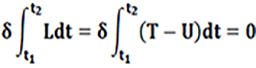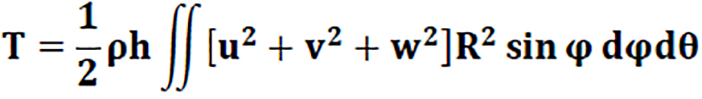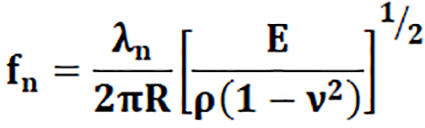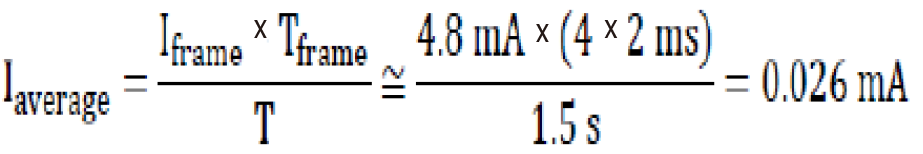Acoustic concept based on an autonomous capsule and a wideband concentric ring resonator for pathophysiological prevention

Abstract

BACKGROUND

Research on the performance of elements constituting our modern environment is constantly evolving, both on a daily basis and on technological basis. But to date, the response of the system to the expectations of the population remains too modest.

AIM

To elaborate an ultrasonic technique to scan and evaluate in-vivo physiological properties by coupling sensors and multilayer biological tissues model.

METHODS

A low-frequency ultrasonic method (around a frequency of 32 KHz) based on the use of an innovative autonomous ultrasonic capsule as a miniaturized elementary spherical sensor (1 cm of diameter) and micro-rings resonators were examined.

RESULTS

Other their functions as passive listeners for the prevention and diagnosis in physiopathology of the respiratory and laryngeal apparatus, these micro-resonators coupled to the ultrasonic capsule through biological tissues (the body) are capable of evaluating the effects of aggression of the environment on human metabolism.

CONCLUSION

This would allow consequently the detection of some potential diseases at an early stage, even in people who still represent no symptoms, which would permit an early treatment and a higher chance of cure.

Key Words: Sensor; Capsule; Acoustics; Ring resonators; Biological tissues

Core tip: Research on the performance of elements constituting our modern environment is constantly evolving, both on a daily basis and on technological basis. But to date, the response of the system to the expectations of the population remains too modest. The current trend lies in the very definition of performance, seen mainly from the point of view of optimizing the service provided to the users. Estimating it, is putting first the medico-technological coherence that will be measured by its capacity to respond to a certain number of needs of both care and comfort.

INTRODUCTION

Studying interactions between acoustic and living fields goes far beyond biological and health impact studies. Within the context of the development or application of treatments, we intend to explore potential innovations motivated by the wide variety of medical challenges.

Obtaining continuous measurements is often more difficult and only a few constraining devices (rectal, esophageal probes, etc.) allow continuous monitoring of the physiological properties of an individual.

Many of the studies have addressed endoscopic ultrasound applications, the majority of which used wired systems. As an example, Lay et al[1] developed a wired ultrasonic imaging capsule for gastrointestinal disorders combining the imaging capabilities of endoscopic ultrasound. The work of Peng et al[2] focuses more on ultrasonic ablation of cancer cells and He et al[3] combines’ optoacoustic interference for these endoscopic characterizations. To this end, de Groen[4] presents a panoramic view of endoscopic features and associated applications.

The evaluations of the quantities concerned are based on significant parameter uncertainty, which constitutes an undeniable field of application for statistical approaches. In this context and taking into account the limitations and the difficulty of some applications (morphology, age, etc.), our work focused on the development of an autonomous information system able to collect data on physiological variations or body composition using vibratory waves. This means of exploration combines endoscopy and ultrasound.

The layout of a sensor network embedded in the body is at the heart of concerns in terms of wave propagation, wave/tissue interactions, and biocompatibility of the radiating elements.

The objective of this work was partly to contribute to the development of innovative radiating structures close to the body (sensors radiating inside the body and through multilayer tissues). The development of a new autonomous ultrasound capsule-based scanning method associated with multilayer models represents a very important challenge given the difficulty of experimental implementation in the low frequency band. This work aimed to obtain conclusive results to assess exposure compared to the thresholds tolerated normatively and to propose an alternative method in order to set a better soft diagnosis to avoid in the limit of possible exposure regarding the harmful radiation [Magnetic resonance imaging (MRI), X-rays, etc.]. This device makes it possible to monitor continuously the physiological evolution (mechanical stress, etc.) and consequently reduce, by alert, the risks in situations considered as extreme.

To improve understanding and quantify the interaction process of evolving tissue characteristics in real conditions, a new low-frequency ultrasonic technique with a miniaturized elementary spherical sensor that behaves as a point source (capsule) was examined. This source was coupled through tissues to receivers spatially identified on the body and adapted, by their concentric ring shapes, to the central vibration frequency of the transmitter. The use of a dedicated algorithm allowed data logging and triggering of alerts if the threshold of a critical value was exceeded.

Using an embedded electrical control architecture, this “capsule” can simultaneously manage tasks such as acoustic transmission/reception, remote data storage and/or telecommunication, as well as provide extended autonomy, which is currently not available for discrete elements.

Given the technical characteristics of such resonators, the randomly distributed capsule network will be able to deliver useful information regarding the evolution of the mechanical state of a dynamic system. A threshold regarding the desired state set by the user must be included in the device in order to reach optimal decisions.

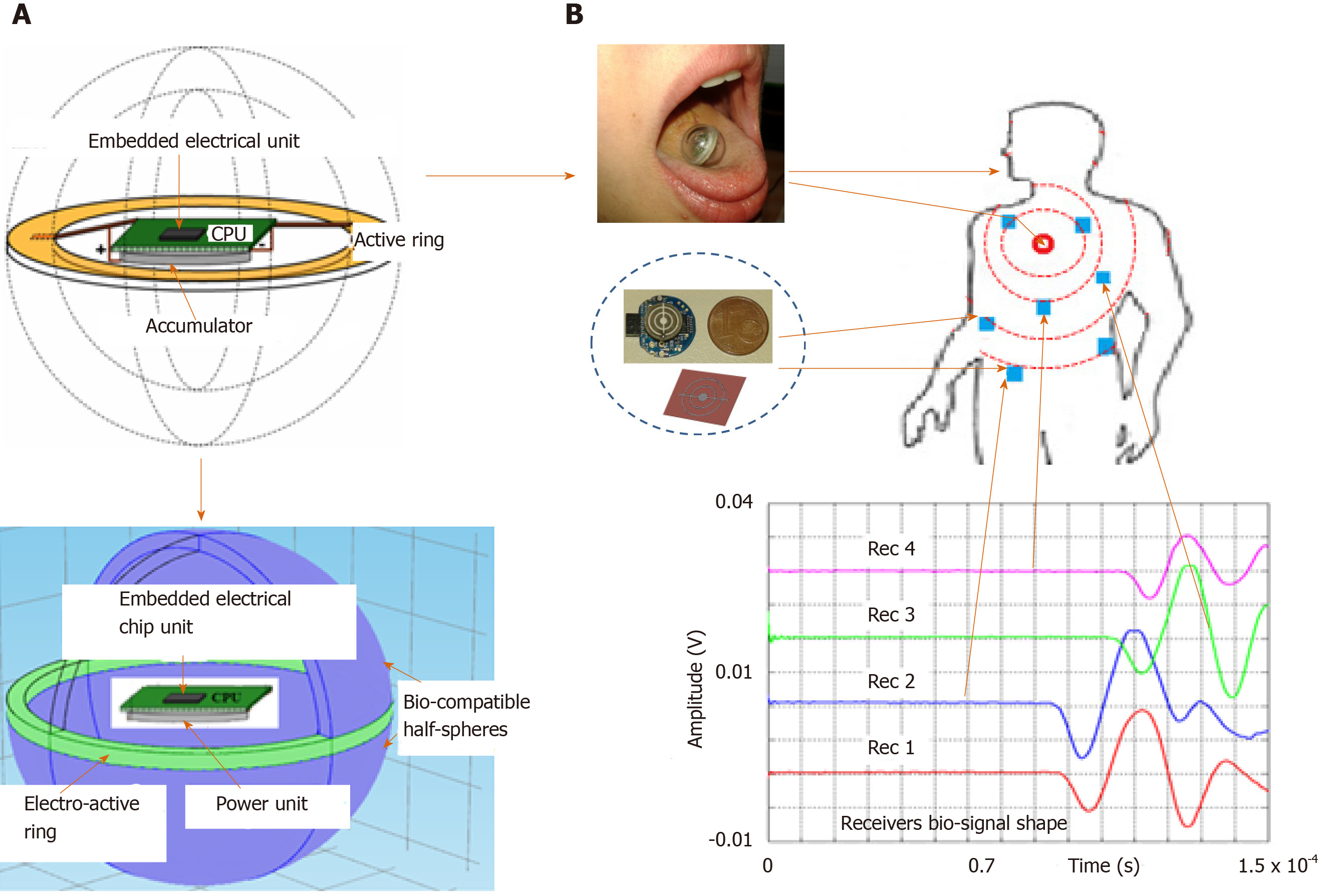
Figure 1 shows the global concept and the potential application in the biological domain. However, for legislative and regulatory reasons, the concept studied in this paper was validated using biological tissues of animal origin and agar as a coupling medium because its physical properties are close to those of human physiological fluid.

Figure 1 Illustration of the global concept based on a mobile ultrasonic capsule resonator as an emitter and a thin layer concentric rings resonators playing the role of receivers. A: The global concept based on a mobile ultrasonic capsule resonator; B: An emitter and a thin layer concentric rings resonators playing the role of receivers.

MATERIALS AND METHODS

Resonator devices

Integrated emitter capsule sensor: Contrary to most ultrasonic transmission techniques, our goal was to obtain a low-frequency acoustic point source to generate a spherical wave in the medium. To do this, we used a piezo element for which the frequency was optimized to bring the entire mechanical structure of a small sphere into resonance. The radius of the sphere is smaller than the acoustic wavelength generated in the medium so it can be considered as an acoustic point source.

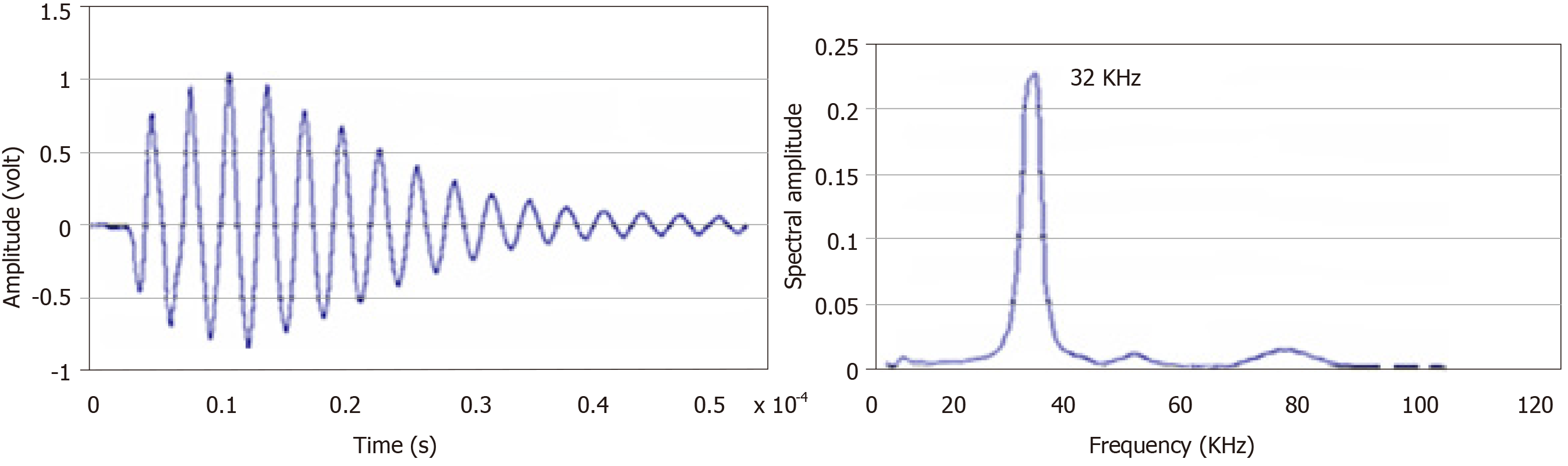
The resonator is a closed spherical shell composed of two hemispheres made of a biocompatible material. Its inner radius is about 8 mm and it is about 2 mm thick[5]. Resonance of the overall structure occurs as a result of the vibrations produced by a piezoelectric ring (0.5 mm thick) clamped between the two hemispheres (Figure 1A). This configuration offers a good compromise between a frequency of around 32 kHz suitable for the “ultrasonic” exploration of complex dispersive media and easy decoupling of the mechanical vibration frequency from the process (background noise) “until then considered as an undesirable parameter”.

Fundamental acoustic vibrational mode: Spherical motion

Relatively few studies have investigated miniaturized spherical resonators. The most recent studies concern an ultrasonic capsule device measuring 1 cm × 2.5 cm developed by Wang et al[6] and Memon et al[7] dedicated to scanning the gastrointestinal tract using ultrasound with an external emission provided by active elements positioned around the capsule. In the same context, Cox et al[8] conducted studies regarding the feasibility of a wired ultrasound capsule endoscopy. Walker[9] and Nasedkin et al[10] developed a theoretical and finite element model of an ultrasonic transducer incorporating spherical resonators. However, a number have been developed over the past decades, especially for studying the properties of gasses and liquids. Mehl et al[11] used a spherical resonator in a frequency range of 4 to 13 kHz to measure the velocity and attenuation of sound in C₂H₄ between 0 and 100 °C and 0.15 to 1.0 MPa. The resonator is made of two aluminum hemispheres with an inner diameter of 127 mm and a thickness of 12.1 mm. He et al[12] developed another spherical resonator to measure sound velocity in the gas phase (argon). The resonator comprises two stainless steel (00Cr17Ni14Mo2 type) hemispheres with an inner radius of 61.77 mm and a working frequency between 1 and 15 kHz. The resonator was placed in a pressurized container that was immersed in a thermos-regulated bath.

Analytical approach

Many studies have been conducted in the field of mechanical vibration of spherical shells for axisymmetric modes. Baker[13], Wilkinson[14], Kalnins[15] and Duffey et al[16], for example, studied the vibration of a macro spherical shell under the effect of transverse shear and rotational inertia.

In what follows, to establish the equations of motion of a spherical shell we considered the fundamental theory of Love based on the Lagrangian formulation. In the case of an undamped system, the Lagrangian “L” is defined as the difference between kinetic “T” and potential “U” energy: L = T – U.

For a dynamic system undergoing a continuously free vibratory motion (t₁ ≤ t ≤ t₂), the equation of motion can be expressed using the Hamilton principle that satisfies the following condition (Formula 1).

Figure formula 1 

For a spherical shape, the kinetic energy is given by Formula 2.

Figure formula 2 

Where h is the thickness of the sphere, ρ is the material density, and (u, v, w) are the deformation of the sphere in spherical coordinates. Based on this model, Wilkinson[14] established, for a thin spherical shell, a cubic polynomial in λ² (frequency parameter) whose solution expresses the vibration modes governing the spherical axisymmetric vibration (without torsion): αλ⁶ - βλ⁶ +βλ⁶ - λ = 0. Where α, β and δ are the dimensional characteristics of the sphere.

The solution of the polynomial of Eq. 4 governs the motion of the spherical structure and can be expressed analytically by the “axisymmetric fundamental resonance mode” which is given by Formula 3, and provides the natural radial frequencies of both the breathing and nth mode of closed spherical shells.

Figure formula 3 

Where R is the radius of the mid-surface of the spherical shell, ρ is the density, E is Young’s modulus, ν is Poisson’s ratio, n is the mode number, and λ_n is a frequency parameter for the vibration mode n given by Formula 4.

Figure formula 4 

Figure 2A shows the natural frequencies of the membrane modes with the following properties: Elastic modulus E = 3300 Mpa, mass density ρ = 1190 kg/m³, Poisson’s ratio ν = 0.39, radius R = 6.7 mm, and thickness h = 2.6 mm.

Figure 2 Natural frequencies of tortionless modes for the sensor and frequency response mode of impedance measurement and finite element analysis. A: Natural frequencies of tortionless modes; B: Frequency response mode of impedance measurement and finite element analysis.

For each value of n ≥ 1, there are three distinct frequencies (three branches or three mode shapes), but only two branches are presented in this part of the study. These two lower and upper branches correspond to the membrane and bending modes, respectively. The mode associated with n = 0 on the membrane branch is called the “fundamental mode”, a pure breathing (elongation) mode of the spherical shell. The results are in good agreement with those of Soedel[17] and Husson[18] and those given by applying the modal analysis to determine the first resonance frequency of the sensor considered (Figure 2B).

Physical concept

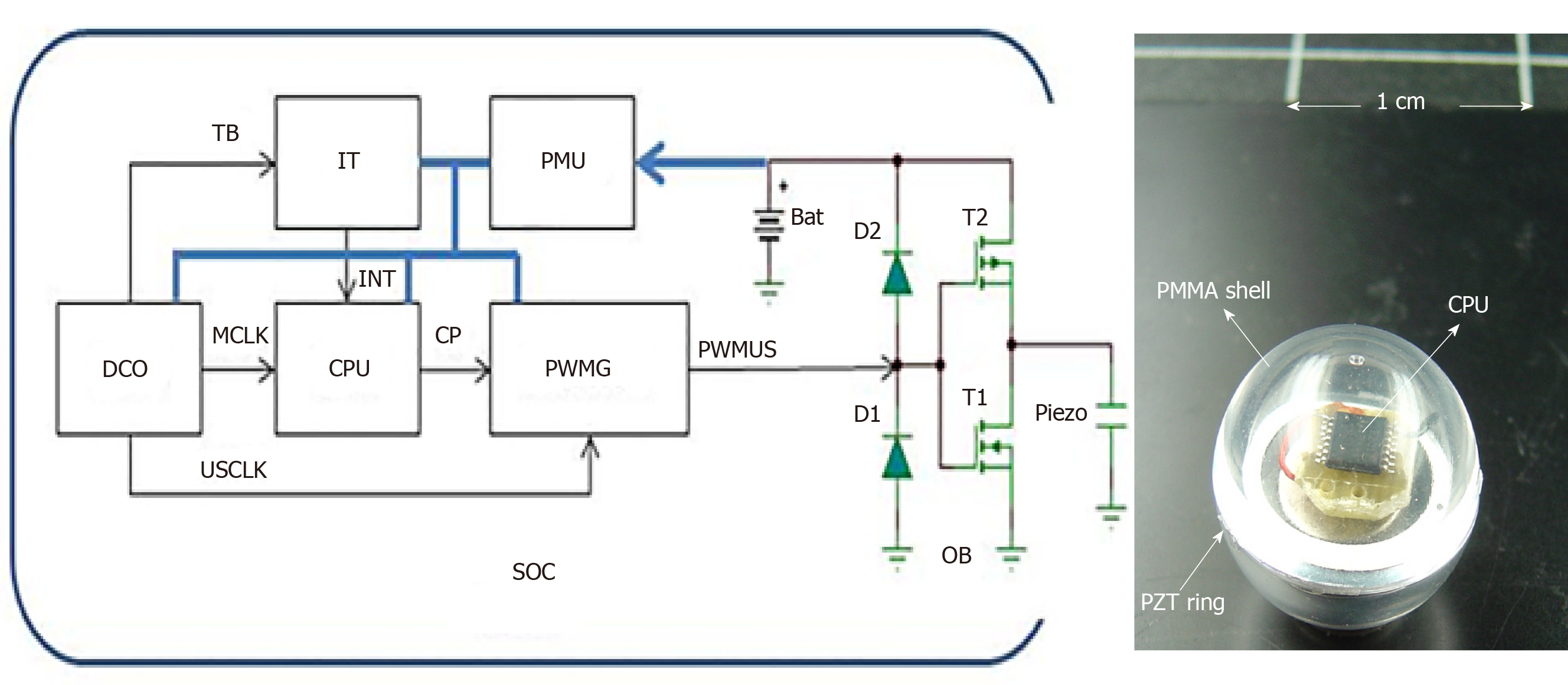
Embedded electrical scheduling unit: An electronic module is inserted into the hollow part of the sphere (Figure 3) to ensure the following tasks of the sensor simultaneously: (1) Structure resonance; (2) Emission-reception control; (3) Encoding algorithm; and (4) Signal processing and data storage.

Figure 3 Architecture of the real-time electrical control system embedded in the physical concept (ultrasonic capsule). DCO: A digital oscillator; CPU: Central processing unit; PMU: Power management unit; PWMG: A coded ultrasonic generator; IT: A task scheduler; OB: An output amplifier.

The electronics are integrated into a chip system that includes a central processing unit (CPU), a digital oscillator (DCO), a task scheduler (IT), a coded ultrasonic generator (PWMG), a power management unit (PMU), an output amplifier (OB), and an accumulator (BAT).

The device was made from a SoC of the MSP430 family from “Texas Instruments”. The MSP430F2012 was chosen for its small size and minimal hardware resources.

The DCO produces three clock sources: A low-frequency clock (TB) set to 12 kHz to produce a stable time base for the task scheduler (IT), a high-frequency clock (MCLK) set to 16 MHz for timing the CPU, and an average frequency clock (USCLK) set to 32 kHz, which is the frequency of the vibrations emitted by the capsule.

At regular intervals (60 ms), the task scheduler (IT) sends an interrupted signal (INT) to the CPU that produces a sequence of width-modulated bit pulses (CP). This bit sequence is both the interrogation signal and the medium identifier of the device. This sequence is modulated by the all or nothing width modulation generator (PWMG) based on the carrier frequency (USCLK). These coded pulses are amplified by the output amplifier (OB) before being applied to the piezoelectric element. A 3V accumulator (BAT) powers the unit. A PMU provides an economical supply for the various elements of the chain to ensure minimum energy consumption and maximum autonomy of the device.

Autonomies and energy balance: One of the goals was to design a sensor with a broad operating range that could be injected into a process (mixer, tank, etc.) for monitoring purposes, so we carried out measurements on power consumption during active sensor emissions. Electrical consumption was determined using a 10-Ohm shunt placed in series in the battery. The battery voltage and the voltage across the shunt were measured using differential isolation amplifiers. Both signals were recorded on a digital oscilloscope (Figure 4), which was also used to calculate the instantaneous power consumption of the device.

Figure 4 Power consumption during a 0111 frame emission (code 7).

Outside the frame of bits, the consumption was insignificant except for the low-frequency clock (TB) and the task scheduler (IT). The CPU, PWMG generator, output amplifier, and other clocks were stopped.

For the transmission of the frame of bits, all the elements were “in operation” and the consumption was maximal. This consumption is due mainly to the central unit that works even during the spaces between bits as these spaces are managed by software. Minor overconsumption occurs when the PWMG generator is turned on transmitting a 0 or 1 level, but this consumption is marginal.

Based on different recordings, we can see that the average consumption of the system for a bit frame is relatively independent of the code transmitted: Iframe ≈ 4.5 mA.

The average current consumed over a time frame T_frame = 15 ms repeated periodically every T = 1.5 s is then Formula 5.

Figure formula 5 

Another possibility could be a more sophisticated IT task management scheduler that can turn the system unit “off” during these spaces. In this case, the emission of code 15 (1111 and maximum power requirement) would produce an average current drain between two frames (Formula 6).

Figure formula 6 

Thin layer concentric ring receiver sensor

The usual ultrasonic concept is generally based on the use of a resonant piezoelectric transducer vibrating in thickness mode. As the resonant frequency of a transducer is inversely proportional to its size, it becomes greater and greater for low frequencies around 100 kHz.

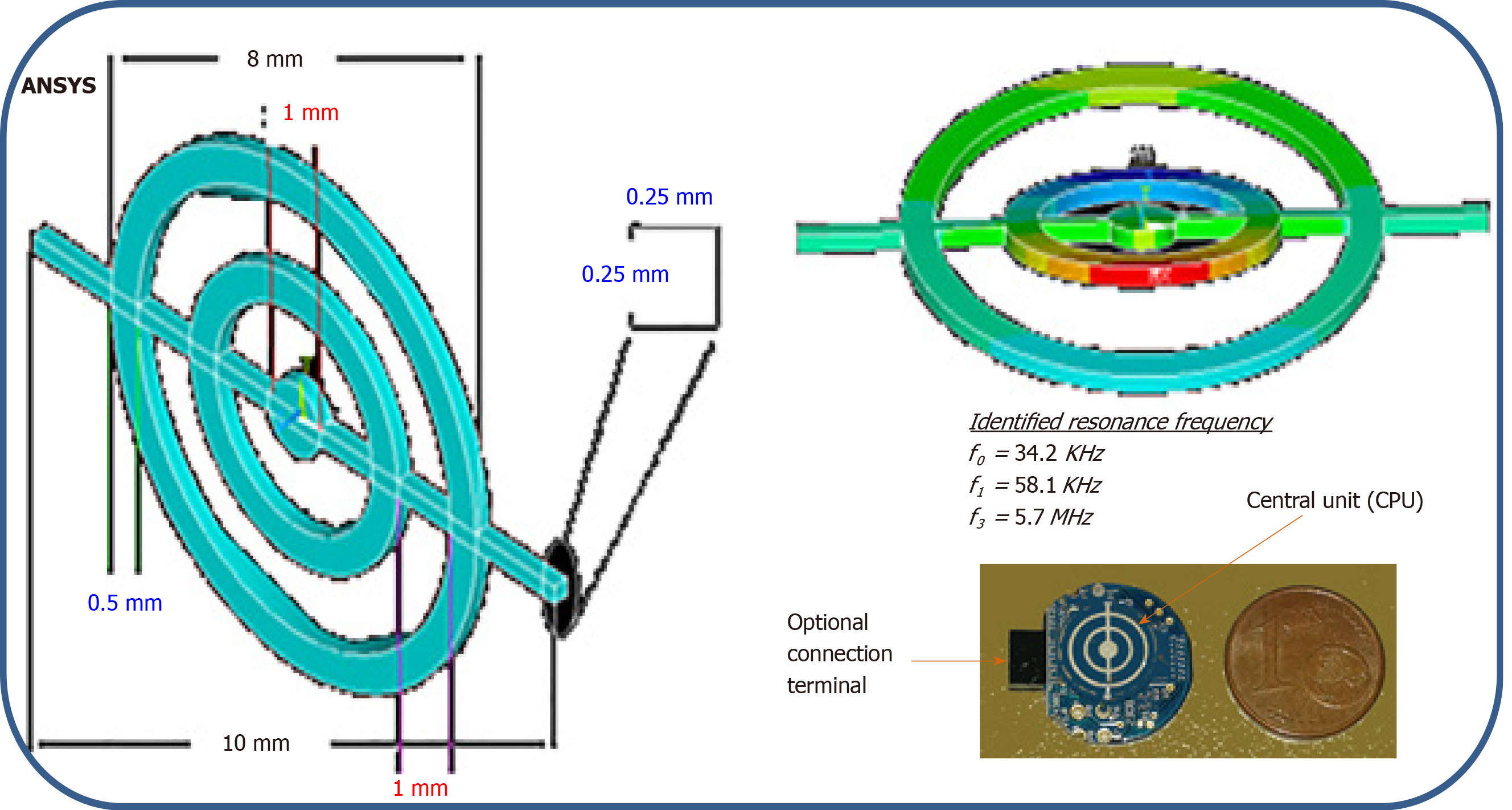
Our aim was to obtain miniaturized low-frequency acoustic broadband receivers with a frequency component of the same order as the resonance frequency of the capsule. To do this, a different procedure from the classic sensor design was used. The new technique was based on the principle of setting in resonance small, thin concentric rings (Figure 5).

Figure 5 Numerical and physical concept of a micro acoustic sensor based on the use of the vibrational motion of a resonator comprised of concentric rings.

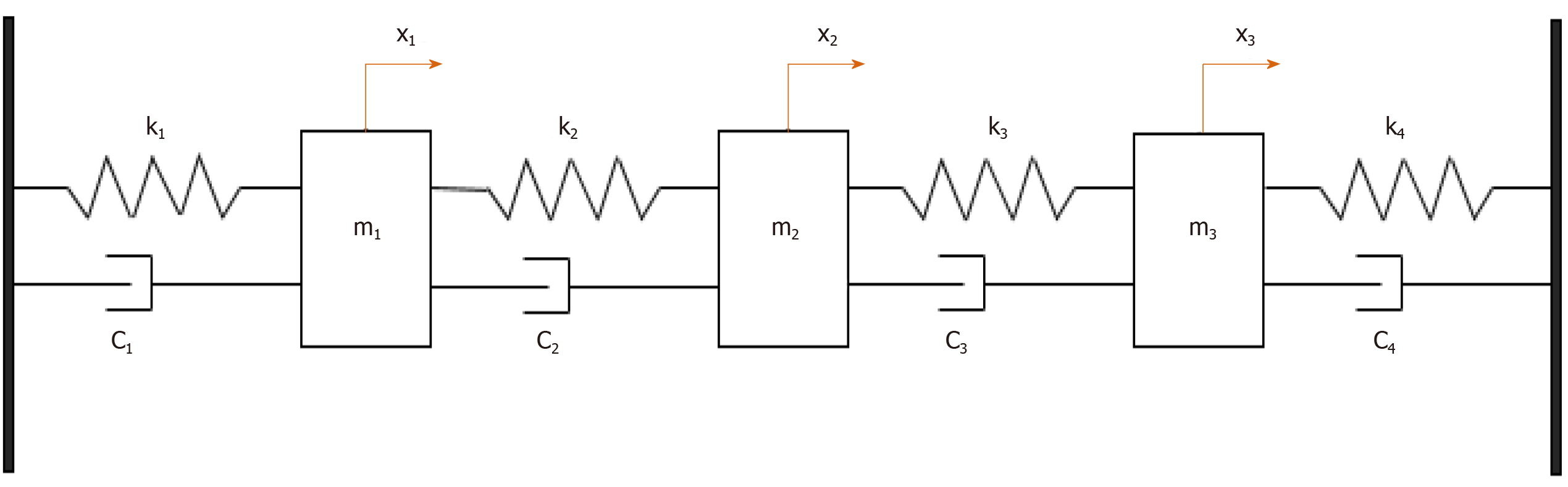
To validate the approach, the mechanical behavior (Figure 6) was assessed and the study was completed with a numerical step using the finite elements method to characterize the resonator vibration modes and visualize the corresponding distortions when the structure was excited. The concordance enabled the use of the experimental device to receive waves coupled with the body or tissues.

Figure 6 Mechanical equivalent of the micro acoustic sensor consisting of an assembly of masses (xi) interposed between systems of springs (ki) and dampers (Ci). k and c reflect the spring and dashpot characteristics.

From a mechanical point of view, eigenvalues of following equation express the dynamics frequencies of the system: -ω⁶ + 15.107jω⁵ + 4.1015ω⁴ – 33.1020jω³ + 1.1027ω² + 2.1032jω + 25.1036 = 0. So, f₀ = 35 KHz, f₁ = 56 KHz and f₂ = 5.25 MHz. Numerical values: k = 18.104 N/m, c = 0.5, m₁ = 4835.10^-6 kg, m₂ = 1088.10^-8 kg, m₃ = 1813.10^-8 kg.

The physical concept of the micro-receiver is elaborated on the basis of a piezoelectric disk of diameter at the base 10 mm and thickness of 0.25 mm. The central concentric rings are made through an assisted laser engraving system. Other than the physical maintenance of the rings, the central rod allows both electrical polarization and electrical continuity with the central control unit (Figure 5).

RESULTS

Metrological approach

System stability: Before using the composite sensor to characterize a medium reflecting real biological tissues, its performance was validated in a medium with well-known, stable physical properties. For this purpose, we used water as a coupling medium.

At a frequency of 32 kHz, the first mode of vibration emitted by the spherical structure produced the echo diagram presented in Figure 7.

Figure 7 Time and frequency response of the sensor resulting from a short electrical pulse.

Based on the resonance frequency mode, the experiment was conducted in thermos-regulated water (25 °C ± 0.3 °C) in which a network of resonators (one transmitter and some receivers) was placed.

Knowing in-situ information about the state of in-vivo tissues requires the instantaneous position of the receivers to be known. The spatial identification of the transmitter at all times gives access to the history of the latter and consequently provides access to the desired physical state or properties of the environment.

The principle of trilateration makes it possible to know the distance between the transmitter and a given receiver by instantaneously locating the source in motion and consequently determining the relative position of the transmitter with respect to a reference point. Measurements are made by exploiting the relative time of flight of the wave (using zero-crossing protocol) between the mobile transmitter and each receiver in the space considered.

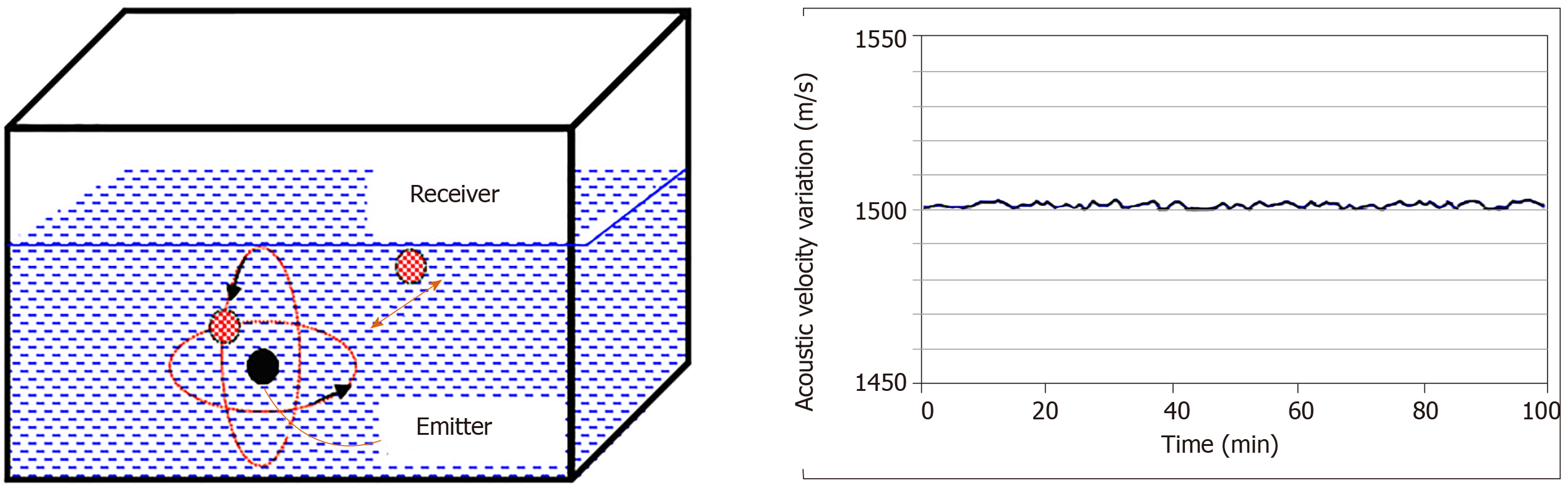
These transducers were coupled to the medium to be characterized and totally submerged. The emitter plays the role of a point source; this phenomenon generates a divergent ultrasonic wave, part of which was measured by receivers located at a regular distance from the transmitter. Figure 8 shows a schematic diagram of the measuring system and the stability plot of the variation in the compressional wave velocity measured at different reception points in the given space. A velocity of around 1545 ± 7 m/s in the Agar used as a coupling medium at 25 °C is always linked to a longitudinal vibration mode.

Figure 8 Schematic illustration of the metrological calibration of the capsule.

In-situ applications

To validate this concept experimentally, we proceeded by two approaches in order to show the field of application and the potential of such system in medical domain. (1) Passive listening approach using concentric micro-sensors for the pathophysiological prevention of the respiratory and vocal apparatus; and (2) Coupling approach (by transmission mode) Capsule/µ-Resonators to estimate the bio-physical evolution properties of multilayers biological tissues resulting from environmental aggression (electromagnetic waves radiation, stress, etc.).

Passive listening approach: This part of study aims to evaluate some larynx physical properties variation through a non-intrusive passive smart listening collar (Figure 9A). The vibratory signal was acquired after each person pronounced the vowel / a /, which reflects the greatest number of vocal cord vibrations modes[19,20]. The latter can provide systematic and in-vivo screening for some laryngeal diseases, including laryngeal cancer, by spectro-temporal analysis of the voice signal resonance. This would allow consequently the detection of these diseases at an early stage, even in people who still represent no symptoms, which would permit an early treatment and a higher chance of cure.

Figure 9 Passive listening approach. A: Physical concept of the micro-resonator acoustic prevention system; B: Spectrograms showing the different frequency components weights for two extreme physiological states: a healthy case and a cancerous state; C: Graphical interface of connected system showing the morphological diagram of signal issued from each category.

For that, micro resonators collar is implemented and is used to carry a detailed examination on four different categories of people: Healthy cases, subjects with laryngeal cancer, those suffering from inflammatory polypus, and the ones having chronic laryngitis. Figure 9B shows the spectrograms of the two extreme physiological cases: A healthy state versus a cancerous one. In our application, one hundred patients with an average age of 53 years of whom 20% were women were diagnosed in the same context but separately.

Figure 9C gives an idea about the display of data and the classification of categories in a real environment. It shows an example of the graphical interface implemented providing the time signature of the signals for each of the above-mentioned patient categories:

The ENT examination shows that in a healthy subject the laryngeal pathway is normal with good mobility of the vocal cords (A). The autocorrelation function (of the time signal) is a sin function; it is maximal at the intercept and contains several secondary periodic lobes resulting from the periodicity of the vibration of the vocal cords.

For a person with cancer (B), the temporal plot is irregular (random) and the spectrum is limited to low frequencies due to a significant decrease in and even total absence of vibration of the vocal cords.

As for subjects with inflammatory polyps or chronic laryngitis (C and D), the temporal plot contains some irregularities but also shows some similarities with the temporal plot of healthy patients. Additionally, the spectrum contains high frequencies but with lower values than healthy subjects.

Coupling capsule/µ-resonators approach: This approach was carried out on the variation of the wave properties such as velocity and energy absorption of the acoustic wave at reception. Raison of ethical consideration, the parameters were measured through a composite medium made from biological tissues of animal origin embedded in a coupling medium, in this case, “Agar” (Figure 10).

Figure 10 Illustration of the measurement cell showing the spatial distribution of the emitter capsule embedded in the volume of agar at controlled distance of the different bio-tissue samples equipped with micro-resonators receivers.

To measure the evolution over time of the physical state of the biological tissues, we considered four samples of animal origin placed at equal distance (10 cm) from the diagonal crossing where the transmitter was located. The samples were embedded in the agar.

The receivers (Ri; i = 1, 2, 3, 4) in the measurement space, close to the samples, were distributed as follows: R1 – Skin sample 3 mm thick; R2 – Composite sample; skin + muscle (3 mm + 7 mm); R3 - Muscle sample 10 mm thick; and R4 - Reference point (coupling without tissue).

Table 1 summarizes the averages of the physical properties of the different samples. These values were considered as starting values at time (t0) in the measurement process based on the “LabView” acquisition system.

Table 1 Averages of the physical properties of the different samples.

	Agar (0.5%)	Skin	Muscle
E	25 kPa	30 MPa	480 MPa
G	148 kPa	0.58 MPa	0.14 MPa
kg/m3	≅ 1	1.3	1.57
	0.5	0.3	0.31

Given the dependence of the ultrasonic velocities on the physical properties of the samples (e.g., compression and shear modulus), the curves on Figure 11 shows the decrease in the compression elastic and shear modulus (E and G) of the samples over time under the effect of aging (applied as physical stress).

Figure 11 Curves showing the evolution of the stress and shear components measured by the experimental approach and compared to the calculated displacement-stress vector (dashed lines) for an incident plane wave in the three-layer medium (agar, skin and muscle).

E and G were measured every two days over a period of 10 d (D) starting from the time of origin t₀ at 25°C.

As the agar is primarily a water incompressible fluid, its Poisson’s ratio is near 0.50 and slight deviations do not significantly affect the results.

To consolidate this variation, the ultrasonic quantification based on matrix stiffness formalism[21] was reported for each measurement showing the response of each layer and the multilayers taking into account the effects of the interfaces and boundary conditions between the layers (agar-muscle-epidermis). Indeed, the multi-layered structure being merged into a single layer, the reflection and transmission coefficients were calculated considering that the whole structure is bounded by fluids. Then, a back-recursive algorithm was applied to compute the displacement vectors amplitudes in each layer, which allows the calculation of acoustic field in every layer based on the angular spectrum approach.

DISCUSSION

The study and design of an autonomous embedded ultrasonic system able to meet a medical need was the main objective of this work. We have proposed a concept of measuring elements based on miniaturized spherical capsule sensors coupled with concentric ring receivers.

A detailed description of the proposed resonator and its vibratory mechanical behavior has been consolidated with a mechanical approach and a numerical approach using finite element analysis.

The physical implementation of the capsule led us to an autonomous vibratory element. The power analysis (impedance and phase) of the overall structure showed very good agreement between the numerical and analytical results.

However, the analysis of the effect of aging factors of tissues on the variation of the acoustic properties gave a coherent view of the mechanical behavior of both the measuring system and the dynamic medium considered. The curves show all the critical phases in a complex evolutionary environment, knowing that there are few techniques, which, under similar conditions, give access to the local physical properties sought.

As a result, this work presents a "soft" and reliable diagnostic system based on the vibratory mechanical behavior of the vocal apparatus. A double interest results in the prospects of such application.

Clinically, this system has been studied and designed to implement an alternative screening method for laryngeal pathologies to save patients from frequent exposure to harmful radiation as RX, MRI, etc.

In terms of prevention, the connected feature of this system offers a means of continuous information on the evolution of a state of health, continuously viewable by a "smart phone" interface, which could lead to a possible early detection of severe laryngeal diseases, especially cancer, giving the subject a higher chance of cure.

ARTICLE HIGHLIGHTS

Research background

Studying interactions between acoustic and living fields goes far beyond biological and health impact studies.

Research motivation

The present manuscript is one of the first reports on a potentially connected "real-time" diagnostic technique, optimizing interactions between acoustic and live fields, providing an autonomous information system capable of collecting data on physiological variations using a soft vibratory wave.

Research objectives

The objective of this work was partly to contribute to the development of innovative radiating structures close to the body (sensors radiating inside the body and through multilayer tissues).

Research methods

A low-frequency ultrasonic method based on the use of an innovative autonomous ultrasonic capsule as a miniaturized elementary spherical sensor and micro-rings resonators were examined.

Research results

Other their functions as passive listeners for the prevention and diagnosis in physiopathology of the respiratory and laryngeal apparatus, these micro-resonators coupled to the ultrasonic capsule through biological tissues are capable of evaluating the effects of aggression of the environment on human metabolism.

Research conclusions

This work presents a "soft" and reliable diagnostic system based on the vibratory mechanical behavior of the vocal apparatus. A double interest results in the prospects of such application.