How to impute study-specific standard deviations in meta-analyses of skewed continuous endpoints?

Abstract

AIM: To compare four methods to approximate mean and standard deviation (SD) when only medians and interquartile ranges are provided.

METHODS: We performed simulated meta-analyses on six datasets of 15, 30, 50, 100, 500, and 1000 trials, respectively. Subjects were iteratively generated from one of the following seven scenarios: five theoretical continuous distributions [Normal, Normal (0, 1), Gamma, Exponential, and Bimodal] and two real-life distributions of intensive care unit stay and hospital stay. For each simulation, we calculated the pooled estimates assembling the study-specific medians and SD approximations: Conservative SD, less conservative SD, mean SD, or interquartile range. We provided a graphical evaluation of the standardized differences. To show which imputation method produced the best estimate, we ranked those differences and calculated the rate at which each estimate appeared as the best, second-best, third-best, or fourth-best.

RESULTS: Our results demonstrated that the best pooled estimate for the overall mean and SD was provided by the median and interquartile range (mean standardized estimates: 4.5 ± 2.2, P = 0.14) or by the median and the SD conservative estimate (mean standardized estimates: 4.5 ± 3.5, P = 0.13). The less conservative approximation of SD appeared to be the worst method, exhibiting a significant difference from the reference method at the 90% confidence level. The method that ranked first most frequently is the interquartile range method (23/42 = 55%), particularly when data were generated according to the Standard Normal, Gamma, and Exponential distributions. The second-best is the conservative SD method (15/42 = 36%), particularly for data from a bimodal distribution and for the intensive care unit stay variable.

CONCLUSION: Meta-analytic estimates are not significantly affected by approximating the missing values of mean and SD with the correspondent values for median and interquartile range.

Key Words: Imputation; Interquartile range; Meta-analysis; Randomized controlled trial; Standard deviation

Core tip: Meta-analyses of continuous endpoints are generally supposed to deal with normally distributed data and the pooled estimate of the treatment effect relies on means and standard deviations. However, if the outcome distribution is skewed, some authors correctly report the median together with the corresponding quartiles. In the present work, we compared methods for the approximation of means and standard deviations when only medians with quartiles are provided. Our results demonstrate that meta-analytic estimates are not significantly affected by approximating the missing values of mean and standard deviation with the correspondent values for median and interquartile range.

INTRODUCTION

Meta-analysis (MA) is a powerful statistical method that merges the results of different studies considering the same outcome variables. The included studies are mainly randomized controlled trials with experimental and control arms. MA aims at assessing the treatment effect size under scrutiny, at identifying sources of heterogeneity among the included studies, at unrevealing patterns behind the available data, and sometimes at identifying new subgroup associations. Some authors believe that MA represents the highest level of evidence to provide recommendations on clinical issues.

Just as many other innovative statistical techniques, MA is still a matter of intense debate, since many of its assumptions are critical and even small violations of them can lead to misleading conclusions[1]. The appeal of MA resides also in the quick and cost-effective way it yields useful pieces of information for clinical decision making. Hence, MAs are published and quoted with an impressive increasing frequency and it seems evident that, despite their limitations, they will continue to play a crucial role in medical decision-making in the foreseeable future.

Meta-analyses of continuous outcomes exploit data with a Gaussian distribution, so that the pooled estimate computation requires the study-specific mean, standard deviation (SD), and sample size of the variable at stake. The easiest way to compare the outcomes of two treatment groups is to evaluate the difference between their means[2]. If measurements are expressed in the same unit, the mean difference between the treatment and control groups can be used. Results from trials in which the same outcome is measured in different units can be compared by using SD units rather than absolute differences[2,3]. However, if data are reported in a limited or incomplete way, it can be difficult or impossible to obtain sufficient information to perform a correct summary of the results. Missing SD and non-compliance in reporting collected data are common limitations in MAs of continuous outcomes.

If the outcome has a skewed distribution, authors often report in the original paper the median together with the 1^st and 3^rd quartiles, rather than the mean with its SD. MA authors arbitrarily combine these study-specific estimates to approximate the missing SD. In addition, some authors combine together means (SD) and medians (1^st and 3^rd quartiles) from different studies.

In this setting, the most immediate question is whether it is legitimate to approximate study-specific means and SDs from study-specific medians and quartiles and how to do it in the most appropriate way.

In the present work we simulated MA of continuous outcomes generated from seven different distributions and we compared four methods to approximate SDs when only study-specific medians and quartiles are available. For each simulation we calculated a pooled estimate by assembling the individual medians and, in turn, all four SD approximations. Finally, we compared these results with those obtained by pooling the individual means and SDs.

To our knowledge, this is the first study on how to impute the study-specific mean and SD in meta-analyses of skewed outcomes. After a failed tentative of comparing results coming from published studies, the present paper compares the available methods making use of both simulations and real-life set-ups to identify the best and the worst SD approximation.

MATERIALS AND METHODS

Simulation algorithm

We generated six datasets of 15, 30, 50, 100, 500, and 1000 trials, respectively. Each trial is based on an equal number of treated and control subjects which is fixed at the number of trials included in the MA under examination. The distributions of the continuous endpoints for the treatment and control groups are generated according to Table 1. The first five scenarios provided the basis for our analysis on simulated data. The last two scenarios of Table 1 represent our real-life data and are randomly extracted from an Italian observational study with more than 7000 patients with cardiovascular disease.

Table 1 Distributions of the continuous endpoint for treatment and control groups.

Scenario	Endpoint distribution
	Treatment group	Control group
Normal	Mean = 5 and SD = 2	Mean = 7 and SD = 2
Standard normal	Mean = 0 and SD = 1	Mean = 0 and SD = 1
Gamma	Alpha = 2 and beta = 5	Alpha = 2 and beta = 7
Exponential	Mean = 5 and lambda = 0.2	Mean = 7 and lambda = 0.14
Bimodal	50% Normal distribution with mean = 5 and SD = 2 and 50% standard normal distribution	50% Normal distribution with mean = 7 and SD = 2 and 50% standard normal distribution
ICU stay	Real-life data	Real-life data
Hospital stay	Real-life data	Real-life data

ICU: Intensive care unit.

In summary, we generated 1695 (15 + 30 + 50 + 100 + 500 + 1000) trials for each of the seven distribution scenarios for a total of 11865 trials. For each trial we calculated the principal measures of position, mean and median, and variability, SD and interquartile range (IQR).

All simulations and analyses were performed using SAS (release 9.2, 2002-2008 by SAS Institute Inc., Cary, NC, United States)[4]. An example of SAS code is reported in Table 2.

Table 2 Example of SAS code to simulate a meta-analysis on 15 datasets with 15 records generated from a Gamma distribution (alpha = 2 and beta = 5 vs alpha = 2 and beta = 7 for the treatment and control groups, respectively).

* q is the assigned library;

**************************************************;

* SIMULATIONS;

**************************************************;

%let s = gamma;

%let ndset = 15;

* Simulation of n = 15 dataset using the Gamma distributions;

%macro simul;

%do q = 1 %to &ndset;

%let seed = %sysevalf(1234567 + &q);

%let num_i = %sysevalf(&ndset);

%let v = %sysevalf(0 + &q);

data s&q;

k = &q;

%do i = 1%to &num_i;

var1 = 5*rangam(&seed,2);

var2 = 7*rangam(&seed,2);

output;

%end;

run;

%end;

* Dataset combining;

data simul_&s;

set

%do w = 1%to &ndset;

s&w

%end;

;

run;

%mend;

%simul;

* Descriptive statistics for each dataset;

ods trace on;

ods output summary = summary_&s;

proc means data = simul_&s mean std median q1 q3;

class k;

var var1 var2;

run;

ods trace off;

data summary_&s;

set summary_&s;

l1 = (var1_Median-var1_Q1)/0.6745;

l2 = (var2_Median-var2_Q1)/0.6745;

u1 = (var1_Q3-var1_Median)/0.6745;

u2 = (var2_Q3-var2_Median)/0.6745;

if l1 > u1 then MeSD_v1_cons=l1; else MeSD_v1_cons=u1;

if l2 > u2 then MeSD_v2_cons=l2; else MeSD_v2_cons=u2;

if l1 > u1 then MeSD_v1_prec=u1; else MeSD_v1_prec=l1;

if l2 > u2 then MeSD_v2_prec=u2; else MeSD_v2_prec=l2;

MeSD_v1_mean=(var1_Q3-var1_Q1)/1.349;

MeSD_v2_mean=(var2_Q3-var2_Q1)/1.349;

* Median difference;

MeD = var1_Median-var2_Median;

*1 conservative estimate of standard deviation;

a1sd = ((MeSD_v1_cons)**2)/NObs;

b1sd = ((MeSD_v2_cons)**2)/NObs;

MeSD_cons=sqrt(a1sd + b1sd);

*2 less conservative estimate of standard deviation;

a2sd = ((MeSD_v1_prec)**2)/NObs;

b2sd = ((MeSD_v2_prec)**2)/NObs;

MeSD_prec = sqrt(a2sd + b2sd);

*3 mean estimate of standard deviation;

a3sd = ((MeSD_v1_mean)**2)/NObs;

b3sd = ((MeSD_v2_mean)**2)/NObs;

MeSD_mean = sqrt(a3sd + b3sd);

*4 Interquartile range;

a4sd = ((var1_Q3-var1_Q1)**2)/NObs;

b4sd = ((var2_Q3-var2_Q1)**2)/NObs;

MeSD_iqr = sqrt(a4sd + b4sd);

* Mean difference and pooled standard deviation;

MD = var1_Mean-var2_Mean;

asd = ((var1_StdDev)**2)/NObs;

bsd = ((var2_StdDev)**2)/NObs;

SD = sqrt(asd + bsd);

drop l1 l2 u1 u2 asd bsd a1sd b1sd a2sd b2sd a3sd b3sd a4sd b4sd;

run;

*************************;

* Meta-analyses;

data sum_&s;

set summary_&s;

keep k NObs MeD MeSD_cons MeSD_prec MeSD_mean MeSD_iqr MD SD qq;

run;

*1 Median and conservative estimate of standard deviation;

data meta_&s.1;

set sum_&s;

model = "Conservative SD";

MDz = MeD;

SDz = MeSD_cons;

w = 1/(SDz**2);

MDw = MDz*w;

keep model k NObs MDz SDz w MDw;

run;

*2 Median and less conservative estimate of standard deviation;

data meta_&s.2;

set sum_&s;

model = "Less Conservative SD";

MDz = MeD;

SDz = MeSD_prec;

w = 1/(SDz**2);

MDw = MDz*w;

keep model k NObs MDz SDz w MDw;

run;

*3 Median and mean estimate of standard deviation;

data meta_&s.3;

set sum_&s;

model = "Mean SD";

MDz = MeD;

SDz = MeSD_mean;

w = 1/(SDz**2);

MDw=MDz*w;

keep model k NObs MDz SDz w MDw;

run;

*4 Median and interquartile range;

data meta_&s.4;

set sum_&s;

model = "IQR";

MDz = MeD;

SDz = MeSD_iqr;

w = 1/(SDz**2);

MDw = MDz*w;

keep model k NObs MDz SDz w MDw;

run;

*Mean and standard deviation (reference);

data meta_&s.5;

set sum_&s;

model = "Reference";

MDz = MD;

SDz = SD;

w = 1/(SDz**2);

MDw = MDz*w;

keep model k NObs MDz SDz w MDw;

run;

proc format;

value model

1 = "conservative SD"

2 = "Less Conservative SD "

3 = "Mean SD "

4 = "IQR"

5 = "Reference"

;

run;

*** Fixed effect model meta-analysis - Inverse of Variance method;

%macro meta_iv;

%do i = 1%to 5;

ods output Summary = somme&i;

proc means data = meta_&s&i sum;

var MDw w;

run;

data somme&i;

set somme&i;

model = &i;

format model model.;

theta = MDw_Sum/w_Sum;

se_theta = 1/(sqrt(w_sum));

lower = theta - (se_theta*1.96);

upper = theta + (se_theta*1.96);

mtheta = sqrt(theta**2);

CV = se_theta/mtheta;

keep model theta se_theta lower upper cv;

run;

%end;

data aaMeta_&s;

set

%do w = 1% to 5;

somme&w

%end;

;

run;

title "distr = &s - k = &ndset";

proc print; run;

%mend;

%meta_iv;

Simulated MA

For each of the six datasets we carried out a series of MAs differing with respect to the method of imputation of the study-specific SD[2], as described in Table 3.

Table 3 Method for imputing the study-specific standard deviation.

Methodnumber	Method name	Mean imputation	Standard Deviation imputation1
0	Reference	Mean	SD
1	Conservative SD	Median	max[(3rd quartile - median)/0.6745; (median - 1st quartile)/0.6745]
2	Less Conservative SD	Median	min[(3rd quartile - median)/0.6745; (median - 1st quartile)/0.6745]
3	Mean SD	Median	(3rd quartile - 1st quartile)/(2 × 0.6745)
4	IQR	Median	(3rd quartile - 1st quartile)

¹The 0.675 is the Z value corresponding to an area of 75% of the standard normal distribution function. IQR: Interquartile range.

For each distribution scenario, 30 MAs were therefore performed (6 datasets × 5 methods).

Each MA was carried out using a fixed effect model by the Inverse-Variance method[3].

The global estimate is the mean difference between treatment and control groups, obtained by pooling individual means and SDs.

Comparison of estimates

For each distribution scenario we computed four standardized estimates, θstand_ijk, calculated as:

θstand_ijk = (θ_ijk - θreference_ijk)/ se(θ_ijk)

for

i = 1, 2, 3, 4; j = 15, 30,..., 1000 and k = 1, 2,…, 7.

where θ_ijk is the pooled mean difference resulting from the performed MA, se(θ_ijk) is the corresponding standard error and θreference_ijk is the global estimate obtained by pooling individual means and SDs for each dataset and distribution scenario.

We obtained a total of 168 standardized estimates (7 distributions × 6 datasets × 4 methods).

Statistical model

After blocking for dataset and distribution, we evaluated if the standardized estimates, calculated by each of the four methods, were different from zero in the framework of a repeated measures model using the mixed procedure implemented in the SAS software. Statistical significance was set at the two-tailed 0.05 level for hypothesis testing. Adjustment for multiple comparisons was performed with Tukey-Kramer, Bonferroni and Scheffé corrections[5,6].

Ranking

To identify which imputation method produced the pooled estimate θ_ijk with the minimum difference from the reference one, θreference_ijk, we ranked each standardized estimate θstand_ijk for each dataset and for each distribution scenario. According to this ranking, we calculated the rate at which each estimate appeared as the best, second-best, third-best, or fourth-best[7] and the area under the cumulative ranking curve[8].

Literature screening

We screened all the best published studies reported in the medical literature on critically ill patients included in the 1^st web based International Consensus Conference[9] to assess which information authors of original papers provided in the case of intensive care unit (ICU) and hospital stay outcome. We contacted the corresponding authors by e-mail when one or more of the following information was missing: Mean, SD, median, 1^st-3^rd quartiles. No manuscript provided all of the information requested and only 3 authors replied to our e-mail and provided the extra information needed.

Statistical analysis

The statistical methods of this study were reviewed by Rosalba Lembo from San Raffaele Scientific Institute, Via Olgettina 60, 20132 Milan, Italy.

RESULTS

Table 4 reports the means and the corresponding unadjusted and adjusted P values to assess the presence of a significant difference from zero. Conservative SD and IQR methods showed the lowest mean difference (with mean standardized estimates equal to 4.5 ± 3.5 for conservative SD and 4.5 ± 2.2 for IQR methods, respectively). The less conservative SD method appeared to be the worst, exhibiting the highest difference from the reference.

Table 4 Comparison of results obtained from the four methods of approximation of study-specific means and standard deviations in a meta-analysis of a continuous outcome.

	Standardized pooled estimate, (standard error)	P value1(unadjusted)	P value1(Tukey-Kramer adjustment)	P value1(Bonferroni adjustment)	P value1(Scheffé adjustment)
Conservative SD	4.5 (3.5)	0.14	0.7	0.9	0.8
Less conservative SD	7.8 (2.9)	0.01	0.056	0.07	0.12
Mean SD	6.1 (3.3)	0.04	0.3	0.6	0.5
IQR	4.5 (2.2)	0.13	0.2	0.4	0.4

¹P values were derived from a test on the “method” effect in a repeated measures model including also adjustment by “dataset” and “distribution” effects. IQR: Interquartile range.

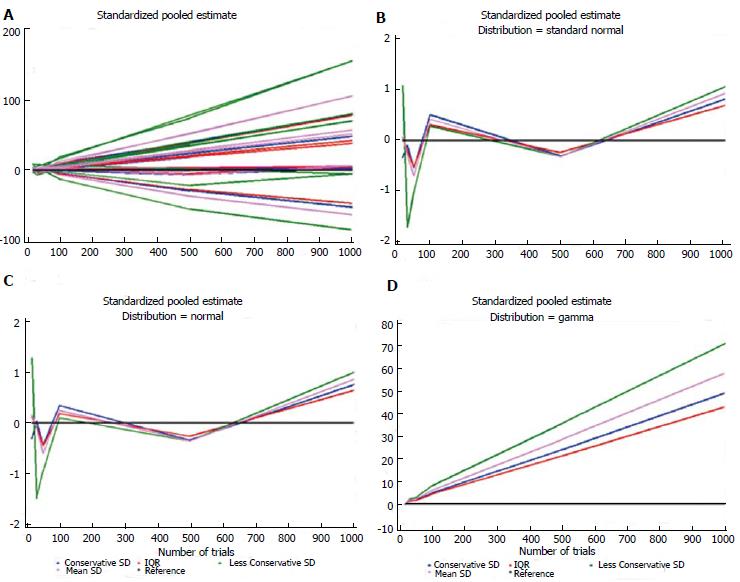
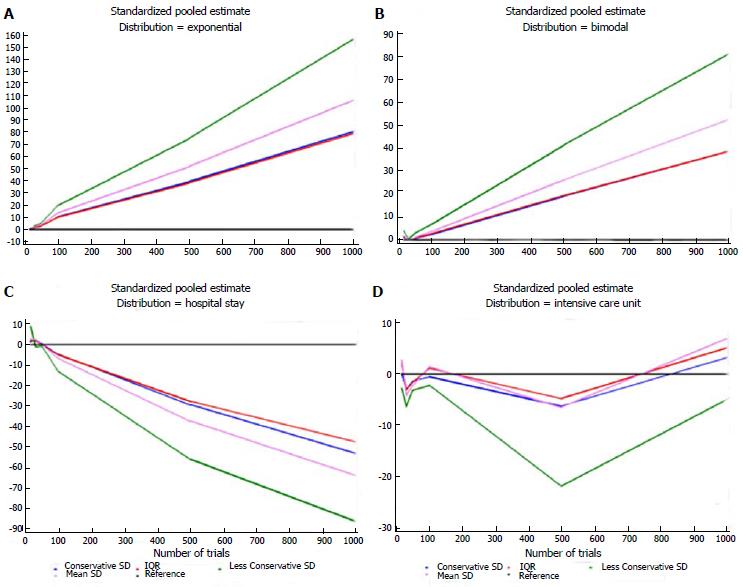
Table 5 shows the estimates for each distribution, dataset, and imputation method and some descriptive statistics. For each distribution, the number of times each standardized estimate ranked first is indicated. The method that ranked first most frequently was IQR (23/42 = 55%), particularly when the data were generated according to the Standard Normal, Gamma, and Exponential distributions. The second best is the Conservative SD method (15/42 = 36%), which was particularly suitable for data with a bimodal distribution and for the ICU stay variable. The quartiles at the bottom of Table 5 were similar for these two methods: 1.62 (0.27-4.94) and 1.40 (0.34-4.86), respectively. Figures 1 and 2 show plots of the pooled estimates for all distribution scenarios. The difference between θstand_ijk and reference values increased together with the increased number of trials in each MA.

Figure 1 Value of each standardized estimate, θstand_ijk, for each number of dataset included in the corresponding meta-analysis simulated. A: All distributions together; B: Normal (mean = 5 and SD = 2 for the treatment group; mean = 7 and SD = 2 for the control group); C: Standardized Normal; D: Gamma (alpha = 2 and beta = 5 for the treatment group; alpha = 2 and beta = 7 for the control group). The X-axis represents the number of studies (datasets) included in the meta-analysis. For each approximation method (blue line for the conservative estimate of SD, green line for the less conservative estimate of SD, pink line for the mean estimate of SD, and red line for the interquartile range), the Y-axis reports the difference between the standardized estimate and the reference (black line). IQR: Interquartile range.

Figure 2 Value of each standardized estimate, θstand_ijk, for each number of dataset included in the corresponding meta-analysis simulated. A: Exponential (mean = 5 and lambda = 0.2 for the treatment group; mean = 7 and lambda = 0.14 for the control group); B: Bimodal (50% Normal distribution (with mean = 5 and SD = 2) and 50% Standardized Normal for the treatment group; 50% Normal distribution (with mean = 7 and SD = 2) and 50% standardized normal for the control group); C and D: Real distribution of intensive care unit stay and hospital stay of an Italian cardiology dataset with 7471 patients. The X-axis represents the number of studies (datasets) included in the meta-analysis. For each approximation method (blue line for the conservative estimate of SD, green line for the less conservative estimate of SD, pink line for the mean estimate of SD, and red line for the interquartile range), the Y-axis reports the difference between the standardized estimate and the reference (black line). IQR: Interquartile range.

Table 5 Absolute differences between standardized estimates, θstand_ijk, calculated by means of one of the four methods (conservative SD, less conservative SD, mean SD and interquartile range), and the reference.

Distributionscenario	Dataset	Conservative SD	Less Conservative SD	Mean SD	IQR
Normal	15	-0.310	1.274	0.149	0.110
Normal	30	0.029	-1.483	-0.109	-0.081
Normal	50	-0.434	-0.946	-0.599	-0.444
Normal	100	0.340	0.095	0.243	0.180
Normal	500	-0.336	-0.357	-0.353	-0.261
Normal	1000	0.754	0.989	0.860	0.638
No. of times of beginning first in the ranking1		2	1	0	3
Standard normal	15	-0.335	1.072	0.062	0.046
Standard normal	30	-0.101	-1.710	-0.290	-0.215
Standard normal	50	-0.535	-1.013	-0.690	-0.511
Standard normal	100	0.502	0.281	0.416	0.308
Standard normal	500	-0.306	-0.314	-0.317	-0.235
Standard Normal	1000	0.814	1.054	0.923	0.684
No. of times of beginning first in the ranking1		1	1	0	4
Gamma	15	-0.283	0.054	-0.119	-0.088
Gamma	30	1.441	2.229	1.846	1.368
Gamma	50	1.795	2.929	2.218	1.644
Gamma	100	4.915	8.193	6.070	4.500
Gamma	500	24.081	35.799	28.753	21.314
Gamma	1000	49.089	71.072	58.012	43.002
No. of times of beginning first in the ranking1		0	1	0	5
Exponential	15	-0.150	-0.163	-0.157	-0.116
Exponential	30	1.880	2.958	2.301	1.706
Exponential	50	2.948	4.975	3.707	2.748
Exponential	100	10.213	19.490	13.493	10.002
Exponential	500	39.546	74.955	51.913	38.481
Exponential	1000	80.605	157.083	106.593	79.016
No. of times of beginning first in the ranking1		0	0	0	6
Bimodal	15	1.142	4.114	1.751	1.298
Bimodal	30	0.079	0.356	0.096	0.071
Bimodal	50	0.545	3.051	1.110	0.823
Bimodal	100	2.405	6.849	3.650	2.706
Bimodal	500	19.156	41.495	26.212	19.431
Bimodal	1000	38.825	81.301	52.527	38.938
No. of times of beginning first in the ranking1		5	0	0	1
ICU stay	15	0.076	-2.816	2.667	1.977
ICU stay	30	-3.011	-6.341	-4.201	-3.114
ICU stay	50	-1.361	-3.162	-2.163	-1.603
ICU stay	100	-0.58	-2.205	1.393	1.032
ICU stay	500	-6.218	-21.788	-6.462	-4.790
ICU stay	1000	3.162	-5.020	6.801	5.042
No. of times of beginning first in the ranking1		5	0	0	1
Hospital stay	15	1.437	8.948	2.777	2.058
Hospital stay	30	2.603	-1.088	2.595	1.924
Hospital stay	50	0.297	-0.839	-0.055	-0.041
Hospital stay	100	-4.674	-13.063	-6.734	-4.992
Hospital stay	500	-29.239	-55.703	-37.170	-27.554
Hospital stay	1000	-52.720	-85.673	-63.453	-47.038
No. of times of beginning first in the ranking1		2	1	0	3
1st quartile		0.337	1.023	0.368	0.273
Median		1.399	2.944	2.190	1.624
3rd quartile		4.855	12.034	6.666	4.942
Total number of times of beginning first in the ranking1		15	4	0	23

¹The ranking procedure was based on differences in absolute value. Number of times that each standardized estimate ranked as for first, for each simulated distribution. Median (interquartile range) of overall standardized estimate distributions. IQR: Interquartile range.

Table 6 reports the rates of occurrence as best, second-best, third-best and fourth-best, for the four imputation methods. The conservative SD and IQR methods most often appeared as best or second-best (cumulative frequencies: 35/42 and 41/42 respectively), and the less conservative SD and mean SD methods as third- or fourth-best. The less conservative SD method was identified as the worst method as it had by far the highest number of fourth positions. Even when it ranked first, the θstand_ijk was very similar to the IQR method, which is consistently suitable for any distribution scenario.

Table 6 Absolute and relative frequencies of occurrence of the four methods to approximate study-specific means and standard deviations in a meta-analysis of a continuous outcome n (%).

	No. of firstranking	No. of second ranking	No. of third ranking	No. of fourth ranking
Conservative SD	15 (35.7)	20 (47.6)	3 (7.1)	4 (9.5)
Less Conservative SD	4 (9.5)	1 (2.4)	1 (2.4)	36 (85.7)
Mean SD	0	3 (7.1)	37 (88.1)	2 (4.8)
IQR	23 (54.8)	18 (42.9)	1 (2.4)	0

IQR: Interquartile range.

Figure 3 shows the areas under the cumulative ranking curve for each imputation method. IQR method yields the largest area.

Figure 3 Area under the cumulative ranking curve for the four methods to approximate mean and standard deviation in a meta-analysis of continuous outcome. IQR: Interquartile range.

DISCUSSION

The aim of our work was to clarify how to best impute study-specific mean and SD when only the median and 1^st and 3^rd quartiles are provided.

It is a notoriously good practice to report information on medians and quartiles for skewed distributions but standard meta-analytic approaches require study-specific means and SDs, so that careful evaluation of the best trade-off between these two approaches is needed.

This issue is of prominent interest when dealing with MA, but few scientific works addressed this topic. Hozo et al[10] described two formulas for estimating the mean from the median, range, and sample size values. Pigott[11] discussed and examined how to deal with missing data (studies, effect size, and methodological information) during MA. Furukawa et al[12,13] reported on the imputation of the missing response rate from the mean ± SD[12] and suggested that borrowing the missing SD from other studies included in the MA may be a valid solution[13]. Thiessen Philbrook et al[14] compared results from MAs that either were restricted to available data or imputed the missing variance with one of four methods (P values, nonparametric summaries, multiple imputation, or correlation coefficients). Robertson et al[15] highlighted and evaluated different ways to include in MAs studies in which the treatment effect was not provided. Weibe et al[16] conducted a systematic review of methods for handling missing variances in MAs of continuous outcomes and classified the relevant approaches into eight groups: algebraic recalculation, approximate algebraic recalculation, study-level imputation, study-level imputation from nonparametric summaries, study-level imputation of correlation (for change-from-baseline or crossover SD and to calculate the design effect for cluster studies), MA-level imputation of overall effect, MA-level tests, and no-imputation methods. Finally, Stevens[17] gave an overview of the Bayesian approach to deal with missing data in MA. However, authors who carry out MAs rarely adopt similar methods in their current clinical practice.

In the present study, we showed that MA pooled estimates are not significantly affected by approximating the missing study-specific mean and SD with the corresponding median and IQR, in both simulated and real-life set-ups. In comparison with the other methods, we found that the Median-IQR method has extra advantages, since it is the simplest one and it makes no assumption on the underlying distribution of the data. Furthermore, we showed how the use of a less conservative approximation of SD can bias the meta-analytic pooled estimate when authors work with skewed data. Nevertheless, it is well known that median and mean values are very different as the data distribution is skewed[2].

Our study has several limitations. First, we did not perform a sensitivity analysis with the random effects model. However, since data were generated from the same distribution for each trial, we decided to apply fixed effect models. Second, we did not analyze mixed set-ups in which study-specific means and SDs are available for some studies and others are imputed. Third, we worked only on trials where the number of treated/control subjects was equal to the number of studies included in the MA. It follows that we did not consider set-ups with many studies and few subjects or vice versa. Although we present several distribution scenarios, the choice of their parameters was arbitrary. However, the performance is not expected to change with different parameters.

It is not surprising that many papers report median and IQR, rather than mean and SD. Actually this is considered good practice when dealing with non-normally distributed data. As an example, since the distributions of ICU or hospital stay are skewed, it might be worth using median and IQR when setting up any MA with these end-points.

Conclusion

Our work supports the procedure of using study-specific medians and quartiles to impute means and standard deviations. This avoids the dangerous practice of not including in the MA studies with missing information. Nevertheless, we recognize that, in order to improve the quality of future MAs, authors of research papers should report as much information as possible at least for concerning their primary outcomes. We suggest that authors who use median and interquartile range in MAs with continuous endpoints, perform a sensitivity analysis in which trials not providing study-specific means and SDs are excluded.

COMMENTS

Background

Meta-analyses (MAs) of continuous outcomes exploit data with a Gaussian distribution, so that the pooled estimate computation requires the study-specific means, standard deviations (SDs), and sample sizes. However, should data be reported in a limited or incomplete way, it can be difficult or impossible to obtain sufficient information to perform a correct summary of the results. Missing standard deviations and non-compliance in reporting collected data are common limitations in MAs of continuous outcomes. At the simpler level, an interest emerged as to the opportunity and the best way to approximate on study-specific means and SDs from study-specific medians and quartiles.

Research frontiers

The aim of the work was to clarify how to best impute study-specific mean and SD when only the median and 1^st and 3^rd quartiles are provided. The authors compared the available methods in simulated and real-life set-ups to identify the best and the worst one. In the present study, authors showed that MA pooled estimates are not significantly affected by approximating the missing study-specific mean and SD with the corresponding median and interquartile range. Among the four methods proposed, the Median-IQR method has the extra advantages since it is the simplest one and that makes no assumption on the underlying distribution of the data.

Innovations and breakthroughs

For the first time, to our knowledge, this manuscript provides a list of four available approximation methods in MAs of skewed outcomes. The authors became aware of these methods in the clinical practice and we strongly believe in the good practice to report information on medians and quartiles when a distribution is skewed. However, standard meta-analytic approaches require study specific means and SDs and it was natural to us to find out a compromise between these two needs. This issue is important when carrying out a MA, but few scientific works addressed this topic. Authors described formulas and estimating procedures to work with missing data in an MA, in either frequentist or Bayesian approach. However, authors who carry out MAs rarely adopt similar methods in their current clinical practice.

Applications

The work gives support to the procedure of using study-specific medians and quartiles to impute means and SDs in an MA of skewed outcome. This avoids the dangerous practice of not including in the MA studies with missing information.

Terminology

Approximation: An estimate of the value of a quantity to a desired degree of accuracy; Conservative estimate: Estimate that avoids excess in approximating the quantity or worth of the list of (potentially infinite) values identified; Distribution: List of the values in a population, or sample, with the corresponding frequency or probability of occurrence; Estimate: A value (a point estimate) or range of values (an interval estimate) to a parameter of a population on the basis of sampling statistics; Interquartile range: Measure of dispersion around the median given by the difference between the 3^rd quartile and 1^st quartile of the distribution; these quartiles can be clearly seen on a box-plot of the data; Study-specific: Related to a specific study included in a more comprehensive MA (i.e., group of study).

Peer-review

The study addresses a very interesting topic and deals with a major concern for investigators who have to perform a meta-analysis from published studies.