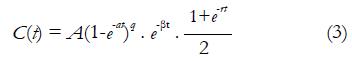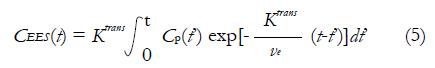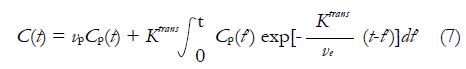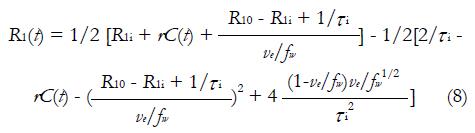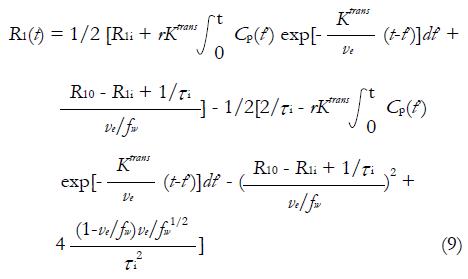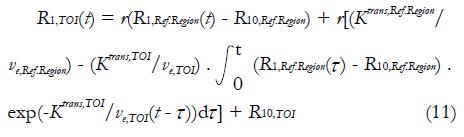Published online Jun 26, 2014. doi: 10.5662/wjm.v4.i2.46
Revised: December 31, 2013
Accepted: February 16, 2014
Published online: June 26, 2014
Processing time: 271 Days and 16.6 Hours
As a noninvasive functional imaging technique, dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) is being used in oncology to measure properties of tumor microvascular structure and permeability. Studies have shown that parameters derived from certain pharmacokinetic models can be used as imaging biomarkers for tumor treatment response. The use of DCE-MRI for quantitative and objective assessment of radiation therapy has been explored in a variety of methods and tumor types. However, due to the complexity in imaging technology and divergent outcomes from different pharmacokinetic approaches, the method of using DCE-MRI in treatment assessment has yet to be standardized, especially for breast cancer. This article reviews the basic principles of breast DCE-MRI and recent studies using DCE-MRI in treatment assessment. Technical and clinical considerations are emphasized with specific attention to assessment of radiation treatment response.
Core tip: Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) has shown great potentials not only in diagnosis, but also in therapy. DCE-MRI is a promising technique for assessing breast cancer radiation treatment due to its inherent sensitivity to the microvascular environment changes. Correlative studies have demonstrated proof concepts of DCE-MRI parameters as potential biomarkers. This article reviews the basic principles of breast DCE-MRI and recent studies using DCE-MRI in breast treatment assessment. Future clinical trials and research works are needed to develop standardized DCE-MRI assessment methods, towards the goal of individualized radiation therapy.
- Citation: Wang CH, Yin FF, Horton J, Chang Z. Review of treatment assessment using DCE-MRI in breast cancer radiation therapy. World J Methodol 2014; 4(2): 46-58
- URL: https://www.wjgnet.com/2222-0682/full/v4/i2/46.htm
- DOI: https://dx.doi.org/10.5662/wjm.v4.i2.46
Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) is an advanced MRI technique that can be used to acquire tissue functional information noninvasively. Following the administration of low molecular weight contrast agent (CA), DCE-MRI is sensitive to microvessel density and vascular permeability differences that can be associated with tumor angiogenesis. Because of this merit, DCE-MRI has been investigated in various oncologic tasks including early diagnosis[1-5], tumor staging[6,7], treatment planning[8,9], and treatment response assessment[10-14]. To assess treatment response, the acquisition of pre-treatment DCE-MRI and post-treatment DCE-MRI scans are required to measure treatment induced changes[14,15]. The change could be quantitatively characterized by a few parameters, which can be derived in the analysis of the DCE-MRI data. For intuitive comparison, simple semi-quantitative information can be obtained from the features of CA concentration evolution curve[16]. The quantitative functional information, such as micro-vascularity permeability, tissue perfusion and cellular density, must be obtained through the application of an appropriate pharmacokinetic model.
As a potential treatment assessment tool, DCE-MRI’s application in breast cancer radiation treatment is of our particular interest. Currently, breast cancer is one of leading incidences in women. Earlier statistics shows one out of eight (12.5%) women will eventually be affected by breast cancer during her lifetime[17]. Since 1990, the death rate of breast cancer have steadily decreased in the United States due to earlier detection and improved treatment[18], and radiation therapy (RT) has become an important technique in breast cancer treatment. Currently, conserving treatment consisting of lumpectomy followed by 6 wk of daily external beam RT has become one of the common treatment regimes in United States. At the same time, some advanced radiation treatment techniques have been proposed to neutralize complexities in breast cancer treatment[19-21]. With its intrinsic superiority in soft tissue contrast and added ability of vascularity measurement, DCE-MRI is a particularly attractive technique in early assessment of breast cancer radiation treatment. The value of using DCE-MRI as a tool for breast cancer radiation treatment assessment relies on the accuracy of quantitative DCE-MRI parameters derived by modeling injected CA pharmacokinetics. However, this is far from straightforward[15]. Some DCE-MRI technical factors will potentially affect the consistency of measured parameters accuracy. For example, differences in pharmacokinetic parameters were observed using different temporal resolution and spatial resolution during image acquisition, and the effect of this tradeoff has yet to be clarified[22]. For clinical consideration, different pharmacokinetic models as well as the interpretation may lead to biased results[23]. Thus, optimizing and standardizing DCE-MRI measurement methods in breast cancer radiation treatment assessment presents as a prerequisite for its clinical application.
In this article, we outline the basic principles in breast DCE-MRI methodology and highlight some relevant techniques and theories in DCE-MRI application. We then present the current findings to date and discuss future directions for DCE-MRI in breast cancer radiation treatment assessment.
DCE-MRI involves a sequential acquisition of magnetic resonance images of tissue before and after the intravenous injection of CA. The CA is usually a small molecular weight compound such as gadopentetate dimeglumine. T2* weighted MRI can be used right after the administration of CA in a few seconds to observe CA first-pass effect which contains perfusion information. Since the first-pass T2* effect is transient, the rapid imaging method performed over a single slice through tissue-of-interest (TOI) is necessary. This is of limited value in breast study because of the necessary larger volume coverage for comprehensive disease morphology assessment[24]. In contrast, T1-weighted DCE-MRI technique is more commonly used in breast cancer research.
The T1-weighted DCE-MRI is usually used over a longer time course in several minutes to measure the accumulation of low molecular T1-shortening paramagnetic CA in the tissue. When CA enters into the tissue-of-interest, the tissue T1 value decreases to an extent which is determined by the CA concentration. A CA concentration evolution curve as a function of time can be acquired from sequentially sampled T1-weighted magnetic resonance images signal intensity at the TOI[25]. The CA concentration at each time point after the administration, C(t), is calculated from longitudinal relaxation rate R1(t) [i.e., the inverse of T1(t)] and the longitudinal relaxation rate R10 before the CA administration with assumed linear dependence[26]:
R1(t) = rC(t) + R10 (1)
r is the longitudinal relaxivity of the CA at certain magnetic field strength. The conventional T1 measurement methods are usually based on inversion recovery spin echo technique. This theory follows a spin inversion and waits for an inversion time TI before the data acquisition. Sometimes, multiple TIs are necessary to accurately estimate a wide range of T1 values[27,28], which is the major contribution of long scan time. To reduce the scan time with uncompromised image quality, many T1 scanning methods have been proposed in brain research domain[29-32]. Another T1 mapping approach is to use multiple flip angles scans. To reduce imaging time, T1 value can be obtained by simple dual flip angles technique[33]. In this method, the ratio of signals of two T1-weighted MR scans with different flip angle φ and ψ is expressed as Ρ. With the general assumption about echo time TE < T2*, T1 value can be calculated by equation (2):
Math 6
TR is denoted as repetition time. equation (2) is used for both R1(t) and R10 calculation. To get R10 information, two additional T1-weighted MR scans must be performed prior to DCE-MRI scan to get T1 baseline information. These two scans with different flip angles are also called T1-calibrations. The following DCE-MRI scans are then acquired with flip angle φ (or ψ), and R1(t) is derived using the DCE-MRI signal at time point t and the T1-calibration with flip angle ψ (or φ) in equation (2). After applying longitudinal relaxation information into equation (1), the CA concentration evolution curve then can be expressed in pixel-by-pixel pattern or volume-of-interest pattern.
For image acquisition, fast T1-weighted sequence is usually adopted for clinical studies. To cover the large breast imaging volume, the imaging time for each frame is relatively longer. Currently, the typical temporal resolution is about 1 min covering the whole breast with three-dimensional fast (3D) spoiled gradient echo (SPGR) dynamic sequence[34,35]. A recent feasibility study demonstrated that the temporal resolution could potentially be enhanced when compressed sensing theory was employed to reconstruct undersamped acquisitions[36].
Semi-quantitative analysis is usually performed on MR signal intensity-time curves or CA concentration evolution curves. In 1998, Daniel et al[37] proposed a patient classification scheme based on visually inspection on MR signal intensity-time curve shape. This scheme defines 5 types of curves. A change in the curve shape type to a higher number is considered as a transformation to a more aggressive type. For a more quantitative approach, the enhancement ratio (ER), which is the percent increase of MR signal intensity at the first acquirement after CA administration (also known as early contrast uptake ECU), is reported as a prediction of tissue physiological environment for routine clinical applications[38]. At the same time, some other quantities, such as initial wash-in rate, the wash-out rate, the maximum point, and extrapolation point were associated as important parameters for the description of curve shape. In the analysis of CA concentration evolution curve, the most frequently used parameter is the initial Area Under the Curve (iAUCτ). iAUCτ denotes the integration of CA concentration evolution curve from injection point (t = 0) to a certain time point (t = τ), and it parameterizes the initial rise of the evolution curve. The concept of onset time representing time lag between CA injection and the appearance of contrast in the tissue is also a commonly used biomarker. Similarly, the gradients of CA uptake and washout as well as the maximum concentration have been investigated in some studies[39,40]. Rigorous mathematic models were also introduced to describe the CA kinetic curve. For example, Fan et al[41] developed an empirical mathematical model (EMM) to parameterize the mathematical behavior of CA concentration evolution curve in transplanted rodent prostate tumors:
Math 7
A is the upper limit of CA concentration, α is the rate constant of CA uptake, β is the overall rate of CA washout, γ is the initial rate of CA washout, and q is the related to the radius of curvature of C(t) at the transition from first-pass to initial washout. Results showed fitted parameters from EMM demonstrated the significant difference between metastatic tumors and nonmetastatic tumors. The same model was also demonstrated to be effective in differentiation of benign lesions from malignant lesions in a human breast study[42].
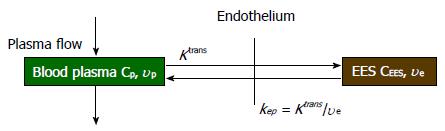
In quantitative analysis, biological parameters depicting vascular permeability, tissue perfusion and extracellular volume fraction can be derived from CA concentration evolution curves by fitting into an appropriate pharmacokinetic model. For breast tissue, the most widely used pharmacokinetic model is the one proposed by Tofts et al[43] in 1991. This two-compartment model describes the bidirectional transendothelial movement of CA between blood plasma and the extravascular-extracellular space (EES) through capillary walls (Figure 1). There are three functional parameters in this model: Ktrans, the transport rate of CA from blood plasma to EES; kep, the transport rate describing the return of CA from EES to blood plasma, and ve, the volume fraction of EES in tissue. The three parameters are related by the equation kep = Ktrans/ve; as a result, Ktrans and ve were reported in most breast DCE-MRI studies. The measured CA concentration C(t) consists of two components:
C(t) = CEES(t) + vpCp(t) (4)
In equation (4), CEES(t) is the CA concentration in EES, Cp(t) is the CA concentration in blood plasma, and vp is the plasma volume fraction in the tissue[44]. The CEES(t) term can also be expressed by the Kety Rate Law as the convolution of Cp(t) with an exponential term[45]:
Math 8
Ktrans is the CA extravasation rate, and ve is the EES volume fraction. Tofts argued that plasma volume fraction vp was very small for many TOIs including breast, so the contribution from Cp(t) in equation (4) is neglected. Then equation (5) can be rewritten as equation (6), which is referred as Standard Tofts Model:
Math 9
The knowledge of Cp(t) is acquired separately from pharmacokinetic model and will be discussed later.
Though the Standard Tofts Model is acceptable in tumors with no large increase in blood volume, the assumption is likely to be invalid in some contexts as blood volume can increase markedly. As a result, some investigators incorporated the effects of possible significant vascular signals[46,47], and equation (6) is added by an additional vascular term:
Math 10
The above equation is frequently called Extended Tofts Model. It was argued that Extended Tofts Model could be reliable in the region with higher vascular signal (abdomen, vp up to 0.3) than the region with lower corresponding signal (brain, vp up to 0.005)[48].
It has to be pointed out that both standard tofts model and extended tofts model are applied to the CA concentration evolution curve C(t), which is oftenly obtained by equation (1). However, the linear dependence of CA concentration and longitudinal relaxation change is not always the case, because this statement is equivalent to assuming that interstitium behaves as a homogeneous solution. To use equation (1), the water exchange from the extravascular intracellular space (EIS) to the EES must be sufficiently fast; but in practice, this is not always guaranteed[49-51]. equation (1) is then modified by taking Bloch equations into account[52]:
Math 11
R1i is the intracellular longitudinal relaxivity, r is the CA longitudinal relaxivity, Cp(t) is the CA concentration in blood plasma, ve is EES volume fraction, τi is the average intracellular water lifetime, and fw is the fraction of water that is accessible to mobile CA. Since the Standard Tofts Model doesn’t rely on the fast water change assumption, the C(t) can be replaced by equation (6), leading to “Fast-Exchange Regime” FXR Model:
Math 12
In practice, R1i is set to R10, and fw is assigned as a constant between 0 and 1. As seen in equation (9), a new variable τi is introduced in FXR Model. In theory, τi is the measurement of cell size. Presumably, as tumor cells apoptose in response to effective treatment, an decrease of τi would be observed. The utility of this parameter has yet to be fully studied[52].
Compared to the two-compartment models, the multi-compartment model has a potential capability of more precise description of pharmacokinetics inside human body. In a pilot study on mammary DCE-MRI, the tumor was modeled by 4 compartments and three of them were accessible to the CA from the central compartment (blood plasma). In addition, a peripheral compartment was introduced to distinguish normal tissues from the tumor[53]. Although the tumor heterogeneity was considered in this model, the in-tumor exchange pattern was still vague. As a nature of the multi-compartment model, the mathematic complexity limits the model’s capacity in breast DCE-MRI study.
Aside from the conventional compartmental models, distributed-parameter (DP) models are seen as another category of DCE-MRI pharmacokinetic model. While the conventional compartmental models have been widely used for more than two decades, they may not possess sufficient realism CA concentration gradients within compartments are assumed to be zero; consequently, CA is assumed to distribute the compartments on arrival instantaneously[54]. On the contrary, DP models describe concentration gradients in vascular compartment as a function of both space and time. Several DP models have been proposed[55,56], but the application in breast clinical study is far from prevalent.
In all pharmacokinetic models mentioned above, the information of CA concentration in blood plasma at each time point Cp(t), which is also known as Arterial Input Function (AIF), must be known prior to the model fitting. This knowledge can be achieved by imaging the major blood pool inside the field of view of images during DCE-MRI scan. For example, the study performed by Rijpkema et al[57] automatically extracted AIF data from DCE-MRI data in head-and-neck region tumor, prostate tumor and brain tumor cases. Unfortunately, such measurement is not feasible for clinical breast cancer studies because no large vasculature is qualified for MR sampling in breast tissue. Though Port et al[58] was able to acquire individual AIF through the visualization of aorta in the breast tumor study, the special procedure was not standardized in clinical protocols. Another approach is to use a population based AIF as an approximation of individual AIF[59,60]. A commonly used model is expressed by a bi-exponential decay [25]:
Cp(t) = D[a1 exp(-m1t) + a2 exp(-m2t)] (10)
D is the CA administration dose as per unit of bodyweight. The two terms in this curve correspond to the fast dynamic equilibrium of CA between blood plasma and EES (represented by a1 and m1) and the slow renal removal of CA (represented by a2 and m2). Several groups of parameter values were reported[44,61].
As can be observed, appropriate AIF is important for accurate quantitative DCE-MRI analysis. However, current approaches in AIF analysis are far from satisfactions. Some investigators have made a lot of efforts in quantitative DCE-MRI analysis in absence of AIF knowledge. Inspired by positron emission tomography, Yankeelov et al[62] proposed a reference region model in 2005. This compartmental model compares the TOI’s CA concentration evolution curve shape to that of a reference region; as a result, the need of AIF information is eliminated. Based on two-compartment model, CA diffuses from blood plasma into EES of the reference region and the TOI respectively, and no exchange of CA exists between the reference region and the TOI. Following equation (1), the longitudinal relaxation signal for TOI, R1,TOI(t), can be derived from reference region’s longitudinal relaxation signal R1,Ref.Region(t):
Math 13
As can be seen, the Ktrans,TOI and ve,TOI must be known in the reference region model. In the mouse tumor study, these values were assigned to the muscle values from publications. But evidently, individual variation of Ktrans and ve values of the selected reference region may result in errors in the values of TOI.
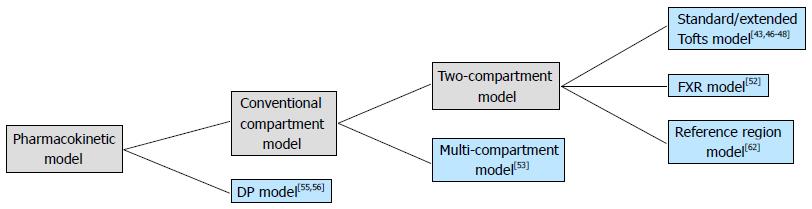
The aforementioned pharmacokinetic models are organized in a hierarchal scheme in Figure 2. To get the functional parameters, appropriate model fitting algorithm must be applied to the DCE-MRI data. For clinical application, the mathematical fitting method should to be fast and accurate. Currently, non-linear Levenberg-Marquart algorithm have been widely used in DCE-MRI studies[63]. Some other fitting methods also have been investigated[64,65]. In some cases, however, the convergence of the fitting algorithm is not guaranteed, thus the accuracy of model fitting may be compromised. Schmid et al[61] raised a semi-parametric approach with which the AIF is convolved with a set of B-splines to produce a design matrix from Bayesian penalized spline models (P-spline). The model parameter is then obtained from the deconvolved response function. At a cost of computation time, the semi-parametric technique was suggested to be more accurate when traditional fitting methods were poor during in vivo validation.
Biologically optimized radiotherapy is a novel technique in which a treatment plan is tailored individually to emphasize variations of pathological context[66]. This approach is made possible by the assessment of treatment response, an indispensable tool in the evaluation of new treatment techniques. As a non-invasive approach, the conventional medical images, including X-ray, ultrasound, computed tomography (CT) and MRI, have been used to evaluate the radiation treatment through the tumor morphological assessment[67]. However, this approach may be of limited value in gauging the radiation treatment efficacy because the tumor may have already developed its radiation resistance when the observation of morphology change is available[68]. In addition, the population-based evaluation standard in patient’s follow-up care after the radiation treatment may not be optimal considering the pathological variations among individuals. The functional analysis of cancer treatment with the possible individualized standards may be a promising approach. The reliability and validity of the functional assessment has been proved in some pilot studies[69,70]. In the radiation treatment context, the non-invasive functional imaging during the early stage of the fractionated therapy would be promising in providing early evidences in treatment management. The unnecessary systemic toxicity and the treatment delays could be avoided as treatment plans could be optimized based on individualized pathological analysis during the treatment regime[71].
The non-invasive function imaging approach is also valuable in the development of advanced treatment techniques. The recent progress in breast cancer radiation treatment allows the accurate delivery of a high dose in one or several fractions. Due to the unconventional dose size and fraction scheme, the biological response of the new techniques should be fully investigated in view of safety and effectiveness. One of the factors of radiation response is tumor oxygenation. Radiobiology theory claims that hypoxia leads to decreased radiation damage induced cell death with an increased level of DNA repair enzymes and radial scavengers[68]. Hypoxia can also cause genome changes which favor the radiation resistant cell population, thus promoting the development of cells with more aggressive phenotypes[66,72-74]. The varying degree of hypoxia is characterized by microvasculature abnormalities, including abnormal microvessel architectures and an increased permeability[75]. Due to the natural sensitivity of the microvascular environment, DCE-MRI measurement parameters were studied in correlation with physiological variables at the breast site. Some of the results are listed in Table 1. Although histopathological studies have shown discrepancies in the outcome, the results suggest that DCE-MRI is suitable for RT assessment of perfusion, permeability and oxygenation[66].
| Ref. | Correlation | Direction of correlation | P | |
| Physiological parameter | DCE-MRI measurement | |||
| Buadu et al[76], 1996 | MVD | Amplitude | + | < 0.01 |
| Slope maximum | + | < 0.01 | ||
| Enhancement Maximum time | - | < 0.01 | ||
| Tumor size | .. | NS | ||
| Stomper et al[77], 1996 | DNA S-phase percentage | Signal enhancement amplitude | .. | NS |
| Signal enhancement rate | .. | NS | ||
| Signal washout | .. | NS | ||
| Hulka et al[78], 1997 | Tumor grade | RSI | + | < 0.01 |
| Matsubayashi et al[79], 2000 | Peripheral-central MVD ratio | Early rim enhancement | + | 0.048 |
| Peripheral-central fibrosis ratio | Early rim enhancement | - | < 0.01 | |
| Central-peripheral fibrosis ratio | Delayed rim | + | 0.013 | |
| Gianfelice et al[80], 2003 | Residue tumor percentage after MRIgFUS | ISI | + | NR |
| MDF | + | NR | ||
| PEI | + | NR | ||
| Su et al[81], 2003 | VEGF | Apparent Vb | .. | NS |
| In-flux rate and distribution volume in interstitial space (VeK1) | .. | NS | ||
| Out-flux rate (K2) | .. | NS | ||
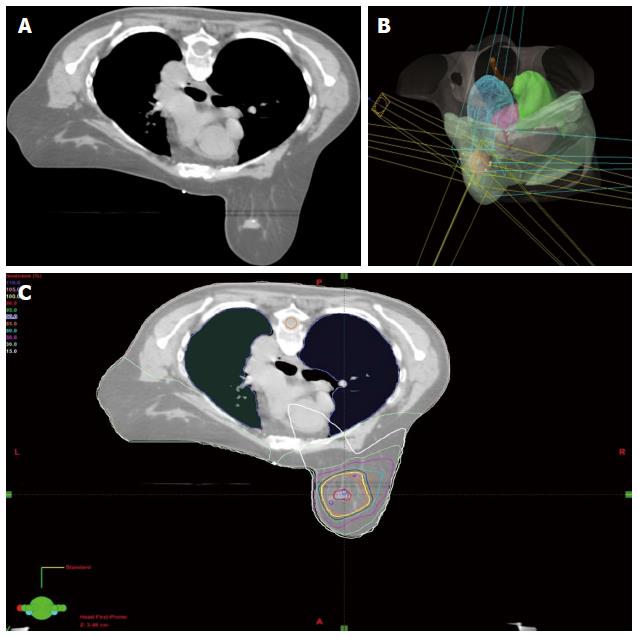
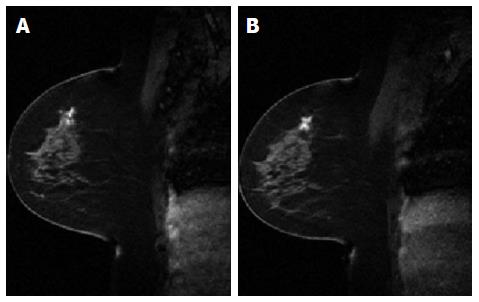
Conventionally, the workflow of RT consists of CT simulation, radiotherapy planning and treatment delivery. Specifically, a breast cancer patient may be scanned with CT simulator to obtain the CT data for treatment planning, as shown in Figure 3A. Based on the CT data, a state-of-the-art RT plan can be developed with a conformal dose distribution, as shown in Figure 3B and 3C. The conventional workflow is summarized in Figure 4A for an easy appreciation. The conventional workflow may, however, miss one critical stage of treatment: treatment assessment. Effective treatment assessment would not only potentially help optimize the radiation treatment strategy, but also could provide valuable insights on the future development of RT. As shown in Figure 4B, the proposed workflow of RT consists of four critical components: CT simulation, radiotherapy planning, treatment delivery and treatment assessment. To assess treatment response using DCE-MRI, one DCE-MRI scan must be obtained before the treatment for baseline data. In addition to standard CT image, the pre-treatment DCE-MRI scan can also be used in target delineation during treatment planning. After radiation treatment, at least one post-treatment DCE-MRI scan must be acquired, and the DCE-MRI parameters derived by the semi-quantitative analysis and/or the quantitative analysis will be compared to the corresponding baseline values. Multiple post-treatment scans allow the longitudinal study of biological response through the parameter dynamic change. Figure 5 illustrates an example of pre-treatment and post-treatment DCE-MRI image comparison from a selected patient. Table 2 lists some studies of the DCE-MRI application in breast cancer radiation treatment assessment. Currently, limited studies have been done in this specific area; further study focusing on breast radiation response assessment is desirable and urgent. In addition to the radiation treatment assessment studies, some representative breast non-radiation treatment studies are also included to provide valuable references and insights on the DCE-MRI application in radiation treatment assessment.
| Ref. | Treatment method | DCE-MRI measurement | Major results |
| Dao et al[82] 1993 | Conserving radiation therapy | Signal intensity | The signal intensity over time in localized fibrosis showed a different pattern from the one in tumor recurrence; early increased signal intensity of the lesion within 3 min after CA administration were observed in recurrent tumors |
| Drew et al[83] 2001 | Neoadjuvant chemoradiotherapy | DCE-MRI image | DCE-MRI detected the presence of residual disease with 100% accuracy |
| Hayes et al[16] 2002 | Neoadjuvant chemotherapy | Ktrans | The absolute change in the Ktrans values correlated negatively with the pretreatment values. The trend is more obvious for responding patients |
| Martincich et al[38] 2004 | Primary chemotherapy | ECU | ECU reduction was associated with a MHR (OR = 2.50, 95%CI: 0.263-23.775); no statistical significance was observed (P = 0.42) |
| Overmoyer et al[84] 2004 | Antiangiogenic drug | Kep | Correlative studies suggested a reduction of tumor Kep and tumor MVD |
| Wedam et al[85] 2006 | Antiangiogenic drug | Ktrans and ve | Ktrans decreased by 34.4% (P = 0.003), and ve was decreased by 14.3% (P = 0.002) after the treatment using bevacizumab |
| Yankeelov et al[52] 2007 | Neoadjuvant chemotherapy | Ktrans, ve, and τi (average intracellular water lifetime) | Significant (P < 0.05) changes were seen in Ktrans and ve; Ktrans in voxels with values in 0.2-0.5 min-1 before treatment were found decreased (P < 0.035) |
| Chang et al[86] 2013 | SBRT | iAUC5min | The mean iAUC5min in GTV increased from 1.93 ± 0.20 mmol-min to 2.31 ± 0.16 mmol-min, about 16% (P = 0.012) after treatment |
Although DCE-MRI is a promising and a powerful tool for assessing treatment response, there are several technical factors to be considered during its clinical implementation, which are crucial to the precise meaning of the derived results. Some key points in DCE-MRI analysis will be briefly discussed below to provide some valuable references for the future work with specific interest on DCE-MRI radiation treatment assessment.
Of all available fast T1 measurement techniques, SPGR imaging with dual flip angles has the superiority in noise efficiency compared with others[30,87]. For high precision T1 measurement which is often necessary in brain studies, multiple flip angle pairs can be adopted to minimize the statistical uncertainty of measured values. In the breast region, acceptable accuracy in T1 value can be achieved if the optimized flip angle pair is found. These two optimal angles are obtained by minimizing T1 variance which comes from the manipulation of the error propagation theory on equation (2) above[33]. In another pilot study of Deoni et al[30], it was argued that optimization of T1 accuracy can be achieved when the product of normalized dynamic range and the fractional signal is maximized. Both methods yield similar optimal flip angle pairs for a certain TR and T1 range. In a simulation study of breast pharmacokinetic parameter estimation[88], both Ktrans and ve were proved to be overestimated if tissue T1 is underestimated; on the contrary, if the T1 is overestimated, Ktrans and ve were less severely underestimated. Specifically, when the ductal native tissue T1 value is underestimated by 65%, Ktrans would be potentially overestimated by 531%. With the same T1 underestimation, ve hit its ceiling threshold with any combination of true Ktrans and ve. As can be seen, optimization of T1 measurement in the DCE-MRI imaging protocol is crucial for accurate quantitative pharmacokinetic analysis.
The error in the optimization of the nominal flip angle is a consequence of B1 inhomogeneity which becomes more prominent at higher magnetic field strength. Kuhl et al[89] proved that for the same breast lesion, the enhancement rate obtained at 3.0 T magnetic field was lower than the respective rate at 1.5 T magnetic field. In the further study[90], B1 field across the bilateral breast MRI field at 3.0 T showed substantial variation, and the variation was independent of coil type. The actual pulse angle varied between 22° and 12.5° over the field of view. Similarly, up to 55% error of nominal flip angle was observed from the healthy volunteer’s B1 maps at 3.0 T[91]. In a breast DCE-MRI study at 3.0 T[92], the median measured B1 field at the right side of breast (in prone position) was reduced by nearly 40% of the expected value. Experiment and simulation showed that a reduced B1 field decreased the ER of dynamic signal curve, and this trend became more prominent when CA uptake was higher. The pharmacokinetic parameters were also affected by B1 inhomogeneity through the varying flip angle[88]. Simulation results showed when the flip angle was underestimated by 55% of its nominal value, Ktrans measurement dropped by 66%, and 55% overestimation of flip angle led to 61% increase of Ktrans. As ve increased, Ktrans sensitivity to the varying flip angle was strengthened. On the other hand, ve showed similar changing pattern except the sensitivity to varying flip angle was independent of Ktrans value. In contrast to 3.0 T, the B1inhomogeneity is less prominent at 1.5 T and is less studied.
The temporal resolution in DCE-MRI is directly dependent on the imaging volume. In a clinically feasible scan which is a part of treatment planning imaging, the frame time covering the whole breast is about 1 min[52]. Theoretically, the reduced temporal resolution would affect the precision of pharmacokinetic analysis by changing the CA concentration evolution curve. In an animal study with 4.7 T magnetic field strength[93], DCE-MRI data was first acquired with 5 s temporal resolution. The data was then downsampled to temporal resolutions ranging from 15 to 85 s. The CA concentration curve showed large discrepancies during the earlier phase. Quantitatively, as temporal resolution decreased, Ktrans was progressively underestimated from 4% to 25%, and ve was overestimated from 1% to 10%. In another simulation study[88], as temporal resolution reduced, Ktrans underestimation was more pronounced at higher nominal values, while ve displayed a 2% minor variation.
One simple way to increase the temporal resolution is to image the lesion only. For radiation treatment assessment purpose, the planning target volume (PTV) is a good candidate, but the knowledge of the TOI must be known prior to scan. As an alternative strategy, undersampling the image with intensive mathematic operation can also increase the temporal resolution[36]. However, since there is no gold standard of true values for pharmacokinetic parameters, the benefit of high temporal resolution imaging is limited. Nevertheless, improvement of high temporal resolution in DCE-MRI will be a continuing interest for researchers.
Ideally, the AIF should be measured from DCE-MRI data for each case, as it varies between individuals in reflection of cardiac output, vascular tone and renal function[15]. Unfortunately, as discussed above, the measurement is not practical in clinical routine imaging because no larger vascularity is within field of view. Besides, the measurement demands high temporal resolution which is not achievable in whole breast imaging[22,59,94,95]. The idealized mathematical model functions are commonly used, though the used functions make no attempt to reflect the true blood supply to the volume of interest[22]. Some other quantitative methods require no AIF information[62,96], but further studies must be done focusing on human breast tissue. In conclusion, one should be aware that AIF methodology leads to potential inaccuracy of pharmacokinetic parameters.
There is no uniform standard of choosing a pharmacokinetic model in quantitative DCE-MRI analysis. The current consensus is that simple models describing the CA transfer rate from the blood plasma to the EES (Ktrans) and the EES volume fraction (ve) should be used for the assessment of vascularity change[15]. The Standard Tofts model and the Extended Tofts model have been widely used due to their simplicity. Despite the limitation of describing the biological picture of CA transport, the two simple models have been proved to be very useful with limited temporal resolution and without accurate AIF information[94]. However, these two models are not identical: in a comparative study into the robustness of compartmental modeling on abdominal tumors and gliomas, the Ktrans calculated by Extended Tofts Model was considerably lower than the value from Standard Tofts Model, while ve maintained similar range in both methods[48].
In pursuit of a more realistic biological mechanism, other models have been evaluated the aspect of accurate parameter reproducibility. For example, initial application of the FXR Model suggested that Ktrans and ve were underestimated by values up to 300% in the assumption of a linear relationship between CA concentration and longitudinal relaxivity change[50,51]. The FXR model was also reported as with the most complete statistical description of DCE-MRI time courses for the patients selected in the study[97]. As a DP model, adiabatic approximation of the tissue homogeneity model (ATH) was proved to be more effective in CA dynamic curve fitting than Tofts models for Time-resolved angiography With Stochastic Trajectories data[98]. However, these comparisons cannot be seen as the evidence of superiority in biological reality. The pharmacokinetic parameter, for example, Ktrans, does not absolutely measure capillary permeability in any model, though it is often assumed to do so; the exact meaning depends on the specific model used for analysis. For instance, the reduction of Ktrans can be interpred as a reduction of blood permeability in ATH model, or a reduction of both blood flow and permeability in Tofts models. As a result, the choice of model reflects the tradeoff between parameters that are either simple in math but lack biological specificity or more physiologically congruent but less stable in math.
Radiation treatment has certain regions of interest including Gross Tumor Volume, Clinical Target Volume and PTV. Data analysis performed over the TOI using the average CA concentration or average signal intensity generates the regional parameters. Though this method is faster, it ignores heterogeneity within the volume of interest. Alternatively, the parameters can be extracted in a pixel-by-pixel pattern within the TOI. The statistics summary such as the mean or median value and standard deviation can be used for assessment[52,90,100]; this method can describe the parameter distributions and limited information about microvessel heterogeneity[15]. In practice, the second method may be too slow for clinical application depending on voxel number and mathematic complexity of model fitting. The challenge can be neutralized by selecting meaningful voxels through certain simple metric[101], or using the advanced GPU acceleration to reduce analysis time[102-105].
DCE-MRI is a promising technique for assessing breast cancer radiation treatment due to its inherent sensitivity to change in the microvessel environment. Correlative studies have demonstrated proof concept of DCE-MRI parameters as potential biomarkers. Presently, an insufficient number of clinical studies have been done in breast cancer radiation treatment. Currently, progress has been achieved in pharmacokinetic model development in pursuit of precise physiology description; however, these methodologies have yet to be fully studied in correlation with clinical outcome in breast cancer radiation treatment. For future work, the study of new pharmacokinetic model with special interests on breast tumor pathology will help improve the interpretation of the DCE-MRI parameter. Advancement in DCE-MRI image acquisition with high spatial and temporal resolution will contribute to the utility of DCE-MRI application in radiation treatment assessment. On the perspective clinical trials are needed with primary aim designed to test standardized DCE-MRI assessment methods for both image acquisition and quantitative biomarker derivation. This is a crucial step towards the goal of individualized radiation treatment planning.
P- Reviewer: Bernhardt GA, Sip M S- Editor: Qi Y L- Editor: A E- Editor: Liu SQ
| 1. | Leach MO, Boggis CR, Dixon AK, Easton DF, Eeles RA, Evans DG, Gilbert FJ, Griebsch I, Hoff RJ, Kessar P. Screening with magnetic resonance imaging and mammography of a UK population at high familial risk of breast cancer: a prospective multicentre cohort study (MARIBS). Lancet. 2005;365:1769-1778. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 650] [Cited by in RCA: 681] [Article Influence: 34.1] [Reference Citation Analysis (0)] |
| 2. | Puech P, Betrouni N, Makni N, Dewalle AS, Villers A, Lemaitre L. Computer-assisted diagnosis of prostate cancer using DCE-MRI data: design, implementation and preliminary results. Int J Comput Assist Radiol Surg. 2009;4:1-10. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 67] [Cited by in RCA: 56] [Article Influence: 3.3] [Reference Citation Analysis (0)] |
| 3. | Goto M, Ito H, Akazawa K, Kubota T, Kizu O, Yamada K, Nishimura T. Diagnosis of breast tumors by contrast-enhanced MR imaging: comparison between the diagnostic performance of dynamic enhancement patterns and morphologic features. J Magn Reson Imaging. 2007;25:104-112. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 75] [Cited by in RCA: 83] [Article Influence: 4.6] [Reference Citation Analysis (0)] |
| 4. | Yuan Y, Giger ML, Li H, Bhooshan N, Sennett CA. Multimodality computer-aided breast cancer diagnosis with FFDM and DCE-MRI. Acad Radiol. 2010;17:1158-1167. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 40] [Cited by in RCA: 26] [Article Influence: 1.7] [Reference Citation Analysis (0)] |
| 5. | Langer DL, van der Kwast TH, Evans AJ, Trachtenberg J, Wilson BC, Haider MA. Prostate cancer detection with multi-parametric MRI: logistic regression analysis of quantitative T2, diffusion-weighted imaging, and dynamic contrast-enhanced MRI. J Magn Reson Imaging. 2009;30:327-334. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 269] [Cited by in RCA: 256] [Article Influence: 16.0] [Reference Citation Analysis (0)] |
| 6. | Hara N, Okuizumi M, Koike H, Kawaguchi M, Bilim V. Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) is a useful modality for the precise detection and staging of early prostate cancer. Prostate. 2005;62:140-147. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 136] [Cited by in RCA: 119] [Article Influence: 6.0] [Reference Citation Analysis (0)] |
| 7. | Delongchamps NB, Beuvon F, Eiss D, Flam T, Muradyan N, Zerbib M, Peyromaure M, Cornud F. Multiparametric MRI is helpful to predict tumor focality, stage, and size in patients diagnosed with unilateral low-risk prostate cancer. Prostate Cancer Prostatic Dis. 2011;14:232-237. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 84] [Cited by in RCA: 75] [Article Influence: 5.4] [Reference Citation Analysis (0)] |
| 8. | van der Heide UA, Houweling AC, Groenendaal G, Beets-Tan RG, Lambin P. Functional MRI for radiotherapy dose painting. Magn Reson Imaging. 2012;30:1216-1223. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 108] [Cited by in RCA: 120] [Article Influence: 9.2] [Reference Citation Analysis (0)] |
| 9. | Nelson SJ. Assessment of therapeutic response and treatment planning for brain tumors using metabolic and physiological MRI. NMR Biomed. 2011;24:734-749. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 74] [Cited by in RCA: 72] [Article Influence: 5.1] [Reference Citation Analysis (0)] |
| 10. | Beauregard DA, Pedley RB, Hill SA, Brindle KM. Differential sensitivity of two adenocarcinoma xenografts to the anti-vascular drugs combretastatin A4 phosphate and 5,6-dimethylxanthenone-4-acetic acid, assessed using MRI and MRS. NMR Biomed. 2002;15:99-105. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 54] [Cited by in RCA: 52] [Article Influence: 2.3] [Reference Citation Analysis (0)] |
| 11. | Benjaminsen IC, Brurberg KG, Ruud EB, Rofstad EK. Assessment of extravascular extracellular space fraction in human melanoma xenografts by DCE-MRI and kinetic modeling. Magn Reson Imaging. 2008;26:160-170. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 43] [Cited by in RCA: 48] [Article Influence: 2.7] [Reference Citation Analysis (0)] |
| 12. | Jarnagin WR, Schwartz LH, Gultekin DH, Gönen M, Haviland D, Shia J, D’Angelica M, Fong Y, Dematteo R, Tse A. Regional chemotherapy for unresectable primary liver cancer: results of a phase II clinical trial and assessment of DCE-MRI as a biomarker of survival. Ann Oncol. 2009;20:1589-1595. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 120] [Cited by in RCA: 147] [Article Influence: 9.2] [Reference Citation Analysis (0)] |
| 13. | Miller JC, Pien HH, Sahani D, Sorensen AG, Thrall JH. Imaging angiogenesis: applications and potential for drug development. J Natl Cancer Inst. 2005;97:172-187. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 258] [Cited by in RCA: 227] [Article Influence: 11.4] [Reference Citation Analysis (0)] |
| 14. | Padhani AR, Leach MO. Antivascular cancer treatments: functional assessments by dynamic contrast-enhanced magnetic resonance imaging. Abdom Imaging. 2005;30:324-341. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 100] [Cited by in RCA: 100] [Article Influence: 5.0] [Reference Citation Analysis (0)] |
| 15. | O’Connor JP, Jackson A, Parker GJ, Jayson GC. DCE-MRI biomarkers in the clinical evaluation of antiangiogenic and vascular disrupting agents. Br J Cancer. 2007;96:189-195. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 415] [Cited by in RCA: 377] [Article Influence: 20.9] [Reference Citation Analysis (0)] |
| 16. | Hayes C, Padhani AR, Leach MO. Assessing changes in tumour vascular function using dynamic contrast-enhanced magnetic resonance imaging. NMR Biomed. 2002;15:154-163. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 227] [Cited by in RCA: 209] [Article Influence: 9.1] [Reference Citation Analysis (0)] |
| 17. | Berg WA. Tailored supplemental screening for breast cancer: what now and what next? AJR Am J Roentgenol. 2009;192:390-399. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 121] [Cited by in RCA: 125] [Article Influence: 7.8] [Reference Citation Analysis (0)] |
| 18. | Heisen M. Understanding quantitative DCE-MRI of the breast: Towards meaningful clinical application. Dissertatie, Technische Universiteit Eindhoven (2010). Available from: http://www.tue.nl/publicatie/ep/p/d/ep-uid/241935/. |
| 19. | Benitez PR, Keisch ME, Vicini F, Stolier A, Scroggins T, Walker A, White J, Hedberg P, Hebert M, Arthur D. Five-year results: the initial clinical trial of MammoSite balloon brachytherapy for partial breast irradiation in early-stage breast cancer. Am J Surg. 2007;194:456-462. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 202] [Cited by in RCA: 182] [Article Influence: 10.1] [Reference Citation Analysis (0)] |
| 20. | Formenti SC, Truong MT, Goldberg JD, Mukhi V, Rosenstein B, Roses D, Shapiro R, Guth A Dewyngaert JK. Prone accelerated partial breast irradiation after breast-conserving surgery: Preliminary clinical results and dose–volume histogram analysis. Int J Radiat Oncol Biol Phys. 2004;60:493-504. [PubMed] |
| 21. | Luini A, Orecchia R, Gatti G, Intra M, Ciocca M, Galimberti V, Veronesi P, Santos GR, Gilardi D, Veronesi U. The pilot trial on intraoperative radiotherapy with electrons (ELIOT): update on the results. Breast Cancer Res Treat. 2005;93:55-59. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 54] [Cited by in RCA: 47] [Article Influence: 2.4] [Reference Citation Analysis (0)] |
| 22. | Parker GJ, Buckley DL. Tracer kinetic modelling for T 1-weighted DCE-MRI. Dynamic Contrast-Enhanced Magnetic Resonance Imaging in Oncology. New York: Springer 2005; 81-92. |
| 23. | Schabel MC, Parker DL. Uncertainty and bias in contrast concentration measurements using spoiled gradient echo pulse sequences. Phys Med Biol. 2008;53:2345-2373. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 178] [Cited by in RCA: 172] [Article Influence: 10.1] [Reference Citation Analysis (0)] |
| 24. | Hylton N. Dynamic contrast-enhanced magnetic resonance imaging as an imaging biomarker. J Clin Oncol. 2006;24:3293-3298. [RCA] [PubMed] [DOI] [Full Text] [Cited by in RCA: 1] [Reference Citation Analysis (0)] |
| 25. | d’Arcy JA, Collins DJ, Padhani AR, Walker-Samuel S, Suckling J, Leach MO. Informatics in Radiology (infoRAD): Magnetic Resonance Imaging Workbench: analysis and visualization of dynamic contrast-enhanced MR imaging data. Radiographics. 2006;26:621-632. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 74] [Cited by in RCA: 72] [Article Influence: 3.8] [Reference Citation Analysis (0)] |
| 26. | Tofts PS, Brix G, Buckley DL, Evelhoch JL, Henderson E, Knopp MV, Larsson HB, Lee TY, Mayr NA, Parker GJ. Estimating kinetic parameters from dynamic contrast-enhanced T(1)-weighted MRI of a diffusable tracer: standardized quantities and symbols. J Magn Reson Imaging. 1999;10:223-232. [RCA] [PubMed] [DOI] [Full Text] [Cited by in RCA: 1] [Reference Citation Analysis (0)] |
| 27. | Ordidge RJ, Gibbs P, Chapman B, Stehling MK, Mansfield P. High-speed multislice T1 mapping using inversion-recovery echo-planar imaging. Magn Reson Med. 1990;16:238-245. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 99] [Cited by in RCA: 104] [Article Influence: 4.3] [Reference Citation Analysis (0)] |
| 28. | Fatouros PP, Marmarou A. Use of magnetic resonance imaging for in vivo measurements of water content in human brain: method and normal values. J Neurosurg. 1999;90:109-115. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 143] [Cited by in RCA: 132] [Article Influence: 5.1] [Reference Citation Analysis (0)] |
| 29. | Deichmann R. Fast high-resolution T1 mapping of the human brain. Magn Reson Med. 2005;54:20-27. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 72] [Cited by in RCA: 78] [Article Influence: 3.9] [Reference Citation Analysis (0)] |
| 30. | Deoni SC, Rutt BK, Peters TM. Rapid combined T1 and T2 mapping using gradient recalled acquisition in the steady state. Magn Reson Med. 2003;49:515-526. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 569] [Cited by in RCA: 540] [Article Influence: 24.5] [Reference Citation Analysis (0)] |
| 31. | Steen RG, Gronemeyer SA, Kingsley PB, Reddick WE, Langston JS, Taylor JS. Precise and accurate measurement of proton T1 in human brain in vivo: validation and preliminary clinical application. J Magn Reson Imaging. 1994;4:681-691. [PubMed] |
| 32. | Zhu DC, Penn RD. Full-brain T1 mapping through inversion recovery fast spin echo imaging with time-efficient slice ordering. Magn Reson Med. 2005;54:725-731. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 62] [Cited by in RCA: 60] [Article Influence: 3.0] [Reference Citation Analysis (0)] |
| 33. | Schabel MC, Morrell GR. Uncertainty in T(1) mapping using the variable flip angle method with two flip angles. Phys Med Biol. 2009;54:N1-N8. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 67] [Cited by in RCA: 73] [Article Influence: 4.3] [Reference Citation Analysis (0)] |
| 34. | Cheng HL. T1 measurement of flowing blood and arterial input function determination for quantitative 3D T1-weighted DCE-MRI. J Magn Reson Imaging. 2007;25:1073-1078. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 58] [Cited by in RCA: 59] [Article Influence: 3.3] [Reference Citation Analysis (0)] |
| 35. | Turnbull LW. Dynamic contrast-enhanced MRI in the diagnosis and management of breast cancer. NMR Biomed. 2009;22:28-39. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 135] [Cited by in RCA: 142] [Article Influence: 8.9] [Reference Citation Analysis (0)] |
| 36. | Wang H, Miao Y, Zhou K, Yu Y, Bao S, He Q, Dai Y, Xuan SY, Tarabishy B, Ye Y. Feasibility of high temporal resolution breast DCE-MRI using compressed sensing theory. Med Phys. 2010;37:4971-4981. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 51] [Cited by in RCA: 50] [Article Influence: 3.3] [Reference Citation Analysis (0)] |
| 37. | Daniel BL, Yen YF, Glover GH, Ikeda DM, Birdwell RL, Sawyer-Glover AM, Black JW, Plevritis SK, Jeffrey SS, Herfkens RJ. Breast disease: dynamic spiral MR imaging. Radiology. 1998;209:499-509. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 156] [Cited by in RCA: 147] [Article Influence: 5.4] [Reference Citation Analysis (0)] |
| 38. | Martincich L, Montemurro F, De Rosa G, Marra V, Ponzone R, Cirillo S, Gatti M, Biglia N, Sarotto I, Sismondi P. Monitoring response to primary chemotherapy in breast cancer using dynamic contrast-enhanced magnetic resonance imaging. Breast Cancer Res Treat. 2004;83:67-76. [PubMed] |
| 39. | O’Flynn EA, DeSouza NM. Functional magnetic resonance: biomarkers of response in breast cancer. Breast Cancer Res. 2011;13:204. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 55] [Cited by in RCA: 53] [Article Influence: 3.8] [Reference Citation Analysis (0)] |
| 40. | Jansen SA, Fan X, Medved M, Abe H, Shimauchi A, Yang C, Zamora M, Foxley S, Olopade OI, Karczmar GS. Characterizing early contrast uptake of ductal carcinoma in situ with high temporal resolution dynamic contrast-enhanced MRI of the breast: a pilot study. Phys Med Biol. 2010;55:N473-N485. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 31] [Cited by in RCA: 28] [Article Influence: 1.9] [Reference Citation Analysis (0)] |
| 41. | Fan X, Medved M, River JN, Zamora M, Corot C, Robert P, Bourrinet P, Lipton M, Culp RM, Karczmar GS. New model for analysis of dynamic contrast-enhanced MRI data distinguishes metastatic from nonmetastatic transplanted rodent prostate tumors. Magn Reson Med. 2004;51:487-494. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 78] [Cited by in RCA: 78] [Article Influence: 3.7] [Reference Citation Analysis (0)] |
| 42. | Fan X, Medved M, Karczmar GS, Yang C, Foxley S, Arkani S, Recant W, Zamora MA, Abe H, Newstead GM. Diagnosis of suspicious breast lesions using an empirical mathematical model for dynamic contrast-enhanced MRI. Magn Reson Imaging. 2007;25:593-603. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 54] [Cited by in RCA: 51] [Article Influence: 2.8] [Reference Citation Analysis (0)] |
| 43. | Tofts PS, Kermode AG. Measurement of the blood-brain barrier permeability and leakage space using dynamic MR imaging. 1. Fundamental concepts. Magn Reson Med. 1991;17:357-367. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1119] [Cited by in RCA: 1103] [Article Influence: 32.4] [Reference Citation Analysis (0)] |
| 44. | Tofts PS. Modeling tracer kinetics in dynamic Gd-DTPA MR imaging. J Magn Reson Imaging. 1997;7:91-101. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1185] [Cited by in RCA: 1138] [Article Influence: 40.6] [Reference Citation Analysis (0)] |
| 45. | Kety SS. Theory of blood-tissue exchange and its application to measurement of blood flow. Methods in medical research. 1960;8:223-227. |
| 46. | Fritz-Hansen T, Rostrup E, Søndergaard L, Ring PB, Amtorp O, Larsson HB. Capillary transfer constant of Gd-DTPA in the myocardium at rest and during vasodilation assessed by MRI. Magn Reson Med. 1998;40:922-929. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 69] [Cited by in RCA: 62] [Article Influence: 2.3] [Reference Citation Analysis (0)] |
| 47. | Henderson E, Rutt BK, Lee TY. Temporal sampling requirements for the tracer kinetics modeling of breast disease. Magn Reson Imaging. 1998;16:1057-1073. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 216] [Cited by in RCA: 207] [Article Influence: 7.7] [Reference Citation Analysis (0)] |
| 48. | Roberts C, Issa B, Stone A, Jackson A, Waterton JC, Parker GJ. Comparative study into the robustness of compartmental modeling and model-free analysis in DCE-MRI studies. J Magn Reson Imaging. 2006;23:554-563. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 125] [Cited by in RCA: 120] [Article Influence: 6.3] [Reference Citation Analysis (0)] |
| 49. | Landis CS, Li X, Telang FW, Coderre JA, Micca PL, Rooney WD, Latour LL, Vétek G, Pályka I, Springer CS. Determination of the MRI contrast agent concentration time course in vivo following bolus injection: effect of equilibrium transcytolemmal water exchange. Magn Reson Med. 2000;44:563-574. [RCA] [PubMed] [DOI] [Full Text] [Cited by in RCA: 1] [Reference Citation Analysis (0)] |
| 50. | Yankeelov TE, Rooney WD, Huang W, Dyke JP, Li X, Tudorica A, Lee JH, Koutcher JA, Springer CS. Evidence for shutter-speed variation in CR bolus-tracking studies of human pathology. NMR Biomed. 2005;18:173-185. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 76] [Cited by in RCA: 65] [Article Influence: 3.3] [Reference Citation Analysis (0)] |
| 51. | Lee J, Shin JS, Park JY, Kwon D, Choi SJ, Kim SJ, Choi IH. p38 mitogen-activated protein kinase modulates expression of tumor necrosis factor-related apoptosis-inducing ligand induced by interferon-gamma in fetal brain astrocytes. J Neurosci Res. 2003;74:884-890. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 150] [Cited by in RCA: 154] [Article Influence: 7.3] [Reference Citation Analysis (0)] |
| 52. | Yankeelov TE, Lepage M, Chakravarthy A, Broome EE, Niermann KJ, Kelley MC, Meszoely I, Mayer IA, Herman CR, McManus K. Integration of quantitative DCE-MRI and ADC mapping to monitor treatment response in human breast cancer: initial results. Magn Reson Imaging. 2007;25:1-13. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 262] [Cited by in RCA: 258] [Article Influence: 14.3] [Reference Citation Analysis (0)] |
| 53. | Port RE, Knopp MV, Hoffmann U, Milker-Zabel S, Brix G. Multicompartment analysis of gadolinium chelate kinetics: blood-tissue exchange in mammary tumors as monitored by dynamic MR imaging. J Magn Reson Imaging. 1999;10:233-241. [RCA] [PubMed] [DOI] [Full Text] [Cited by in RCA: 1] [Reference Citation Analysis (0)] |
| 54. | Larson KB, Markham J, Raichle ME. Tracer-kinetic models for measuring cerebral blood flow using externally detected radiotracers. J Cereb Blood Flow Metab. 1987;7:443-463. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 83] [Cited by in RCA: 82] [Article Influence: 2.2] [Reference Citation Analysis (0)] |
| 55. | Hoffmann U, Brix G, Knopp MV, Hess T, Lorenz WJ. Pharmacokinetic mapping of the breast: a new method for dynamic MR mammography. Magn Reson Med. 1995;33:506-514. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 243] [Cited by in RCA: 228] [Article Influence: 7.6] [Reference Citation Analysis (0)] |
| 56. | St Lawrence KS, Lee TY. An adiabatic approximation to the tissue homogeneity model for water exchange in the brain: I. Theoretical derivation. J Cereb Blood Flow Metab. 1998;18:1365-1377. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 322] [Cited by in RCA: 307] [Article Influence: 11.4] [Reference Citation Analysis (0)] |
| 57. | Rijpkema M, Kaanders JH, Joosten FB, van der Kogel AJ, Heerschap A. Method for quantitative mapping of dynamic MRI contrast agent uptake in human tumors. J Magn Reson Imaging. 2001;14:457-463. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 151] [Cited by in RCA: 136] [Article Influence: 5.7] [Reference Citation Analysis (0)] |
| 58. | Port RE, Knopp MV, Brix G. Dynamic contrast-enhanced MRI using Gd-DTPA: interindividual variability of the arterial input function and consequences for the assessment of kinetics in tumors. Magn Reson Med. 2001;45:1030-1038. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 134] [Cited by in RCA: 129] [Article Influence: 5.4] [Reference Citation Analysis (0)] |
| 59. | Parker GJ, Roberts C, Macdonald A, Buonaccorsi GA, Cheung S, Buckley DL, Jackson A, Watson Y, Davies K, Jayson GC. Experimentally-derived functional form for a population-averaged high-temporal-resolution arterial input function for dynamic contrast-enhanced MRI. Magn Reson Med. 2006;56:993-1000. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 558] [Cited by in RCA: 520] [Article Influence: 27.4] [Reference Citation Analysis (0)] |
| 60. | Le Mignon MM, Chambon C, Warrington S, Davies R, Bonnemain B. Gd-DOTA. Pharmacokinetics and tolerability after intravenous injection into healthy volunteers. Invest Radiol. 1990;25:933-937. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 58] [Cited by in RCA: 57] [Article Influence: 1.6] [Reference Citation Analysis (0)] |
| 61. | Schmid VJ, Whitcher B, Padhani AR, Yang G-Z. A semi-parametric technique for the quantitative analysis of Dynamic contrast-enhanced MR images based on Bayesian P-Splines. New York: Springer 2008; . |
| 62. | Yankeelov TE, Luci JJ, Lepage M, Li R, Debusk L, Lin PC, Price RR, Gore JC. Quantitative pharmacokinetic analysis of DCE-MRI data without an arterial input function: a reference region model. Magn Reson Imaging. 2005;23:519-529. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 217] [Cited by in RCA: 214] [Article Influence: 10.7] [Reference Citation Analysis (0)] |
| 63. | Moré JJ. The Levenberg-Marquardt algorithm: implementation and theory. New York: Springer 1978; 105-116. |
| 64. | Ahearn TS, Staff RT, Redpath TW, Semple SI. The use of the Levenberg-Marquardt curve-fitting algorithm in pharmacokinetic modelling of DCE-MRI data. Phys Med Biol. 2005;50:N85-N92. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 73] [Cited by in RCA: 74] [Article Influence: 3.7] [Reference Citation Analysis (0)] |
| 65. | Sourbron S, Ingrisch M, Siefert A, Reiser M, Herrmann K. Quantification of cerebral blood flow, cerebral blood volume, and blood-brain-barrier leakage with DCE-MRI. Magn Reson Med. 2009;62:205-217. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 199] [Cited by in RCA: 204] [Article Influence: 12.8] [Reference Citation Analysis (0)] |
| 66. | Zahra MA, Hollingsworth KG, Sala E, Lomas DJ, Tan LT. Dynamic contrast-enhanced MRI as a predictor of tumour response to radiotherapy. Lancet Oncol. 2007;8:63-74. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 210] [Cited by in RCA: 214] [Article Influence: 11.9] [Reference Citation Analysis (0)] |
| 67. | Padhani AR. MRI for assessing antivascular cancer treatments. Br J Radiol. 2003;76:S60-S80. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 115] [Cited by in RCA: 103] [Article Influence: 4.9] [Reference Citation Analysis (0)] |
| 68. | Hall EJ, Giaccia AJ. Oxygen Effect and Reoxygenation. Philadelphia: Wolters Kluwer Health 2006; 86-103. |
| 69. | Cella DF, Tulsky DS, Gray G, Sarafian B, Linn E, Bonomi A, Silberman M, Yellen SB, Winicour P, Brannon J. The Functional Assessment of Cancer Therapy scale: development and validation of the general measure. J Clin Oncol. 1993;11:570-579. [PubMed] |
| 70. | Brady MJ, Cella DF, Mo F, Bonomi AE, Tulsky DS, Lloyd SR, Deasy S, Cobleigh M, Shiomoto G. Reliability and validity of the Functional Assessment of Cancer Therapy-Breast quality-of-life instrument. J Clin Oncol. 1997;15:974-986. [PubMed] |
| 71. | Moffat BA, Chenevert TL, Lawrence TS, Meyer CR, Johnson TD, Dong Q, Tsien C, Mukherji S, Quint DJ, Gebarski SS. Functional diffusion map: a noninvasive MRI biomarker for early stratification of clinical brain tumor response. Proc Natl Acad Sci USA. 2005;102:5524-5529. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 498] [Cited by in RCA: 480] [Article Influence: 24.0] [Reference Citation Analysis (0)] |
| 72. | Dachs GU, Tozer GM. Hypoxia modulated gene expression: angiogenesis, metastasis and therapeutic exploitation. Eur J Cancer. 2000;36:1649-1660. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 188] [Cited by in RCA: 178] [Article Influence: 7.1] [Reference Citation Analysis (0)] |
| 73. | Hockel M, Schlenger K, Aral B, Mitze M, Schaffer U, Vaupel P. Association between tumor hypoxia and malignant progression in advanced cancer of the uterine cervix. Cancer Res. 1996;56:4509-4515. [PubMed] |
| 74. | Höckel M, Schlenger K, Höckel S, Aral B, Schäffer U, Vaupel P. Tumor hypoxia in pelvic recurrences of cervical cancer. Int J Cancer. 1998;79:365-369. [RCA] [PubMed] [DOI] [Full Text] [Cited by in RCA: 1] [Reference Citation Analysis (0)] |
| 75. | Denekamp J, Daşu A, Waites A. Vasculature and microenvironmental gradients: the missing links in novel approaches to cancer therapy? Adv Enzyme Regul. 1998;38:281-299. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 671] [Cited by in RCA: 701] [Article Influence: 26.0] [Reference Citation Analysis (0)] |
| 76. | Buadu LD, Murakami J, Murayama S, Hashiguchi N, Sakai S, Masuda K, Toyoshima S, Kuroki S, Ohno S. Breast lesions: correlation of contrast medium enhancement patterns on MR images with histopathologic findings and tumor angiogenesis. Radiology. 1996;200:639-649. [PubMed] |
| 77. | Stomper PC, Herman S, Klippenstein DL, Winston JS, Budnick RM, Stewart CC. Invasive breast carcinoma: analysis of dynamic magnetic resonance imaging enhancement features and cell proliferative activity determined by DNA S-phase percentage. Cancer. 1996;77:1844-1849. [RCA] [PubMed] [DOI] [Full Text] [Cited by in RCA: 1] [Reference Citation Analysis (0)] |
| 78. | Hulka CA, Edmister WB, Smith BL, Tan L, Sgroi DC, Campbell T, Kopans DB, Weisskoff RM. Dynamic echo-planar imaging of the breast: experience in diagnosing breast carcinoma and correlation with tumor angiogenesis. Radiology. 1997;205:837-842. [PubMed] |
| 79. | Matsubayashi R, Matsuo Y, Edakuni G, Satoh T, Tokunaga O, Kudo S. Breast masses with peripheral rim enhancement on dynamic contrast-enhanced MR images: correlation of MR findings with histologic features and expression of growth factors. Radiology. 2000;217:841-848. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 125] [Cited by in RCA: 124] [Article Influence: 5.0] [Reference Citation Analysis (0)] |
| 80. | Gianfelice D, Khiat A, Amara M, Belblidia A, Boulanger Y. MR imaging-guided focused ultrasound surgery of breast cancer: correlation of dynamic contrast-enhanced MRI with histopathologic findings. Breast Cancer Res Treat. 2003;82:93-101. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 110] [Cited by in RCA: 95] [Article Influence: 4.5] [Reference Citation Analysis (0)] |
| 81. | Su MY, Cheung YC, Fruehauf JP, Yu H, Nalcioglu O, Mechetner E, Kyshtoobayeva A, Chen SC, Hsueh S, McLaren CE. Correlation of dynamic contrast enhancement MRI parameters with microvessel density and VEGF for assessment of angiogenesis in breast cancer. J Magn Reson Imaging. 2003;18:467-477. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 130] [Cited by in RCA: 123] [Article Influence: 5.9] [Reference Citation Analysis (0)] |
| 82. | Dao TH, Rahmouni A, Campana F, Laurent M, Asselain B, Fourquet A. Tumor recurrence versus fibrosis in the irradiated breast: differentiation with dynamic gadolinium-enhanced MR imaging. Radiology. 1993;187:751-755. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 150] [Cited by in RCA: 124] [Article Influence: 3.9] [Reference Citation Analysis (0)] |
| 83. | Drew PJ, Kerin MJ, Mahapatra T, Malone C, Monson JR, Turnbull LW, Fox JN. Evaluation of response to neoadjuvant chemoradiotherapy for locally advanced breast cancer with dynamic contrast-enhanced MRI of the breast. Eur J Surg Oncol. 2001;27:617-620. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 79] [Cited by in RCA: 67] [Article Influence: 2.8] [Reference Citation Analysis (0)] |
| 84. | Overmoyer B, Silverman P, Leeming R, Shenk R, Lyons J, Ziats N, Jesberger J, Dumadag L, Remick S, Chen H. Phase II trial of neoadjuvant docetaxel with or without bevacizumab in patients with locally advanced breast cancer. J Clin Oncol. 2004;22:727. |
| 85. | Wedam SB, Low JA, Yang SX, Chow CK, Choyke P, Danforth D, Hewitt SM, Berman A, Steinberg SM, Liewehr DJ. Antiangiogenic and antitumor effects of bevacizumab in patients with inflammatory and locally advanced breast cancer. J Clin Oncol. 2006;24:769-777. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 421] [Cited by in RCA: 408] [Article Influence: 21.5] [Reference Citation Analysis (0)] |
| 86. | Chang Z, Yin F-F, Yoo S, Horton J. Evaluating Radiation-Induced Changes with Diffusion Weighted MRI and Dynamic Contrast Enhanced MRI in Patients with Early Stage Breast Cancer Treated with Stereotactic Body Radiotherapy: Initial Results. Med physics. 2013;40:378. [RCA] [DOI] [Full Text] [Cited by in Crossref: 1] [Cited by in RCA: 1] [Article Influence: 0.1] [Reference Citation Analysis (0)] |
| 87. | Cheng HL, Wright GA. Rapid high-resolution T(1) mapping by variable flip angles: accurate and precise measurements in the presence of radiofrequency field inhomogeneity. Magn Reson Med. 2006;55:566-574. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 256] [Cited by in RCA: 281] [Article Influence: 14.8] [Reference Citation Analysis (0)] |
| 88. | Di Giovanni P, Azlan CA, Ahearn TS, Semple SI, Gilbert FJ, Redpath TW. The accuracy of pharmacokinetic parameter measurement in DCE-MRI of the breast at 3 T. Phys Med Biol. 2010;55:121-132. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 67] [Cited by in RCA: 72] [Article Influence: 4.8] [Reference Citation Analysis (0)] |
| 89. | Kuhl CK, Jost P, Morakkabati N, Zivanovic O, Schild HH, Gieseke J. Contrast-enhanced MR imaging of the breast at 3.0 and 1.5 T in the same patients: initial experience. Radiology. 2006;239:666-676. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 147] [Cited by in RCA: 136] [Article Influence: 7.2] [Reference Citation Analysis (0)] |
| 90. | Kuhl CK, Kooijman H, Gieseke J, Schild HH. Effect of B1 inhomogeneity on breast MR imaging at 3.0 T. Radiology. 2007;244:929-930. [PubMed] |
| 91. | Azlan C, Di Giovanni P, Ahearn T, Prins W, Clemence M, Semple S, Gilbert F and Redpath T. The effectiveness of a bisagittal power optimization approach in the reduction of B1 inhomogeneity in breast MRI at 3T. Proceedings of ISMRM 17th Annual Meeting;. Philadelphia: Wolters Kluwer Health 2009; Curran Associates Inc, 2009: 2106. |
| 92. | Azlan CA, Di Giovanni P, Ahearn TS, Semple SI, Gilbert FJ, Redpath TW. B1 transmission-field inhomogeneity and enhancement ratio errors in dynamic contrast-enhanced MRI (DCE-MRI) of the breast at 3T. J Magn Reson Imaging. 2010;31:234-239. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 56] [Cited by in RCA: 56] [Article Influence: 3.7] [Reference Citation Analysis (0)] |
| 93. | Hasselbalch AL, Angquist L, Christiansen L, Heitmann BL, Kyvik KO, Sørensen TI. A variant in the fat mass and obesity-associated gene (FTO) and variants near the melanocortin-4 receptor gene (MC4R) do not influence dietary intake. J Nutr. 2010;140:831-834. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 58] [Cited by in RCA: 59] [Article Influence: 3.9] [Reference Citation Analysis (0)] |
| 94. | Buckley DL. Uncertainty in the analysis of tracer kinetics using dynamic contrast-enhanced T1-weighted MRI. Magn Reson Med. 2002;47:601-606. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 225] [Cited by in RCA: 217] [Article Influence: 9.4] [Reference Citation Analysis (0)] |
| 95. | Kershaw LE, Cheng HL. Temporal resolution and SNR requirements for accurate DCE-MRI data analysis using the AATH model. Magn Reson Med. 2010;64:1772-1780. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 64] [Cited by in RCA: 69] [Article Influence: 4.6] [Reference Citation Analysis (0)] |
| 96. | Yankeelov TE, Cron GO, Addison CL, Wallace JC, Wilkins RC, Pappas BA, Santyr GE, Gore JC. Comparison of a reference region model with direct measurement of an AIF in the analysis of DCE-MRI data. Magn Reson Med. 2007;57:353-361. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 67] [Cited by in RCA: 74] [Article Influence: 4.1] [Reference Citation Analysis (0)] |
| 97. | Li X, Welch EB, Chakravarthy AB, Xu L, Arlinghaus LR, Farley J, Mayer IA, Kelley MC, Meszoely IM, Means-Powell J. Statistical comparison of dynamic contrast-enhanced MRI pharmacokinetic models in human breast cancer. Magn Reson Med. 2012;68:261-271. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 33] [Cited by in RCA: 30] [Article Influence: 2.1] [Reference Citation Analysis (0)] |
| 98. | Fusco R, Sansone M, Maffei S, Raiano N & Petrillo A. Dynamic contrast-enhanced MRI in breast cancer: A comparison between distributed and compartmental tracer kinetic models. J Biomedical Graphics Computing. 2012;2:23. [RCA] [DOI] [Full Text] [Cited by in Crossref: 16] [Cited by in RCA: 16] [Article Influence: 1.2] [Reference Citation Analysis (0)] |
| 99. | Evelhoch JL, LoRusso PM, He Z, DelProposto Z, Polin L, Corbett TH, Langmuir P, Wheeler C, Stone A, Leadbetter J. Magnetic resonance imaging measurements of the response of murine and human tumors to the vascular-targeting agent ZD6126. Clin Cancer Res. 2004;10:3650-3657. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 140] [Cited by in RCA: 128] [Article Influence: 6.1] [Reference Citation Analysis (0)] |
| 100. | Galbraith SM, Maxwell RJ, Lodge MA, Tozer GM, Wilson J, Taylor NJ, Stirling JJ, Sena L, Padhani AR, Rustin GJ. Combretastatin A4 phosphate has tumor antivascular activity in rat and man as demonstrated by dynamic magnetic resonance imaging. J Clin Oncol. 2003;21:2831-2842. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 279] [Cited by in RCA: 257] [Article Influence: 11.7] [Reference Citation Analysis (0)] |
| 101. | Lee SH, Kim JH, Cho N, Park JS, Yang Z, Jung YS, Moon WK. Multilevel analysis of spatiotemporal association features for differentiation of tumor enhancement patterns in breast DCE-MRI. Med Phys. 2010;37:3940-3956. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 46] [Cited by in RCA: 36] [Article Influence: 2.4] [Reference Citation Analysis (0)] |
| 102. | Chi J, Liu F, Weber E, Li Y, Crozier S. GPU-accelerated FDTD modeling of radio-frequency field-tissue interactions in high-field MRI. IEEE Trans Biomed Eng. 2011;58:1789-1796. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 23] [Cited by in RCA: 24] [Article Influence: 1.7] [Reference Citation Analysis (0)] |
| 103. | Hsu YH, Ferl GZ, Ng CM. GPU-accelerated nonparametric kinetic analysis of DCE-MRI data from glioblastoma patients treated with bevacizumab. Magn Reson Imaging. 2013;31:618-623. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 6] [Cited by in RCA: 8] [Article Influence: 0.6] [Reference Citation Analysis (0)] |
| 104. | Stone SS, Haldar JP, Tsao SC, Hwu WM, Sutton BP, Liang ZP. Accelerating Advanced MRI Reconstructions on GPUs. J Parallel Distrib Comput. 2008;68:1307-1318. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 174] [Cited by in RCA: 90] [Article Influence: 5.3] [Reference Citation Analysis (0)] |
| 105. | Zhuo Y, Wu XL, Haldar JP, Hwu WM, Liang ZP and Sutton BP. Accelerating Iterative Field-Compensated MR Image Reconstruction on GPUs. Biomedical Imaging: From Nano to Macro 2010; Curran Associates Inc, 2010: 820-823 [DOI 10.1109/Isbi.2010.5490112]. |