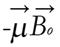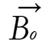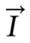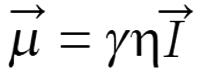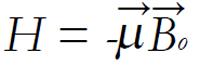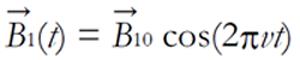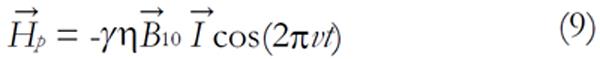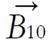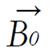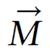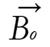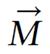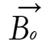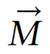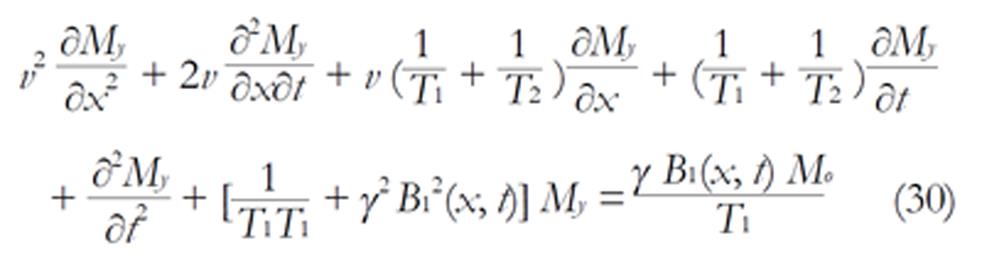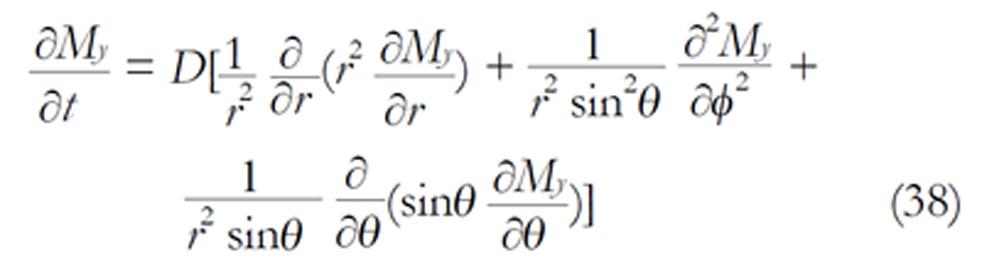Physics and mathematics of magnetic resonance imaging for nanomedicine: An overview

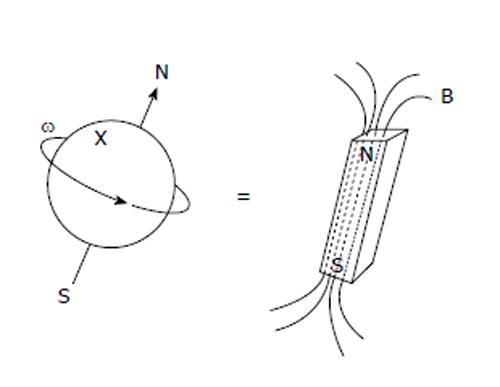
Figure 1 The charged nucleus (for example, ¹H) rotating with angular frequency ω = 2πv creates a magnetic field B and is equivalent to a small bar magnet whose axis is coincident with the spin rotation axis[4].

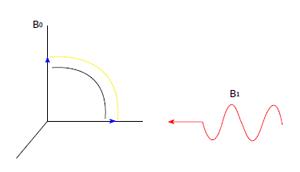
Figure 2 A 90-degree flip of the net magnetization.

Math 1 Math(A1).

Math 2 Math(A1).

Math 3 Math(A1).

Math 4 Math(A1).

Math 5 Math(A1).

Math 6 Math(A1).

Math 7 Math(A1).

Math 8 Math(A1).

Math 9 Math(A1).

Math 10 Math(A1).

Math 11 Math(A1).

Math 12 Math(A1).

Math 13 Math(A1).

Math 14 Math(A1).

Math 15 Math(A1).

Math 16 Math(A1).

Math 17 Math(A1).

Math 18 Math(A1).

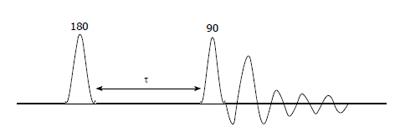
Figure 3 A series of spectra recorded with different values of τ to map out the recovery of the magnetization.

Math 19 Math(A1).

Math 20 Math(A1).

Math 21 Math(A1).

Math 22 Math(A1).

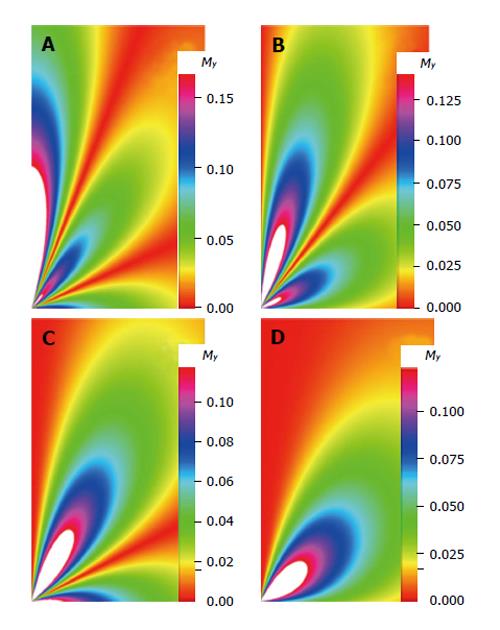
Figure 4 Image from the transverse magnetization as it varies with time, t = 3 ns, and the relaxation parameters τ_l = 5. 1 ns, l = 3.734375 for (A) m = 0; (B) m = 1; (C) m = 2; (D) m = 3.

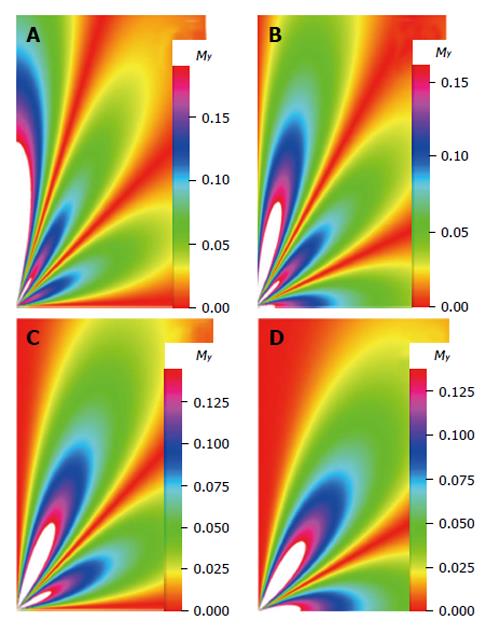
Figure 5 Image from the transverse magnetization as it varies with time, t = 3 ns, and the relaxation parameters τ_l = 6. 3 ns, l = 5.084034 for (A) m = 0; (B) m = 1; (C) m = 2; (D) m = 3.

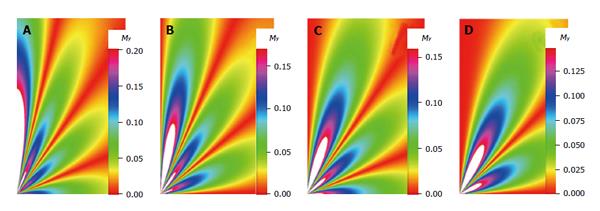
Figure 6 Image from the transverse magnetization as it varies with time, t = 3 ns, and the relaxation parameters τ_l = 7. 1 ns, l = 6.057692 for (A) m = 0; (B) m = 1; (C) m = 2; (D) m = 3.

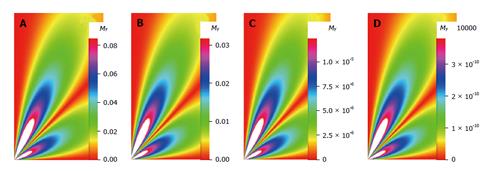
Figure 7 Image from the transverse magnetization as it varies with m = 3, and the relaxation parameters τ_l = 7. 1 ns, l = 6.057692 for (A) t = 5 ns; (B) t = 10 ns; (C) t = 50 ns; (D) t = 150 ns.

Math 23 Math(A1).

Math 24 Math(A1).

Math 25 Math(A1).

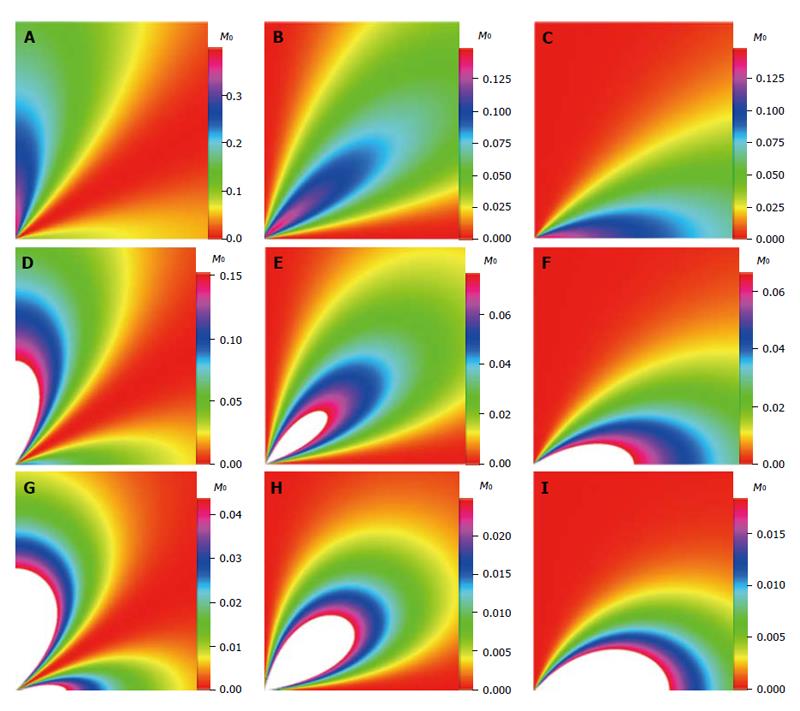
Figure 8 Density maps of M₀ using Equation (8) for l = 2 and (A) m = 0, 0 ≤ R ≤ 2^1/2; (B) m = 1, 0 ≤ R ≤ 2^1/2; (C) m = 2, 0 ≤ R ≤ 2^1/2; (D) m = 0, 0 ≤ R ≤ 8^1/2; (E) m = 1, 0 ≤ R ≤ 8^1/2; (F) m = 2, 0 ≤ R ≤ 8^1/2; (G) m = 0, 0 ≤ R ≤ 32^1/2; (H) m = 1, 0 ≤ R ≤ 32^1/2; (I) m = 2, 0 ≤ R ≤ 32^1/2.