Classical regression equations of spirometric parameters are not applicable for diagnosing spirometric abnormalities in adipotic adults

Abstract

The prevalence of overweighing and obese adults (defined as “adipotic” adults), has markedly increased over the world. A remarkable increase in the adipotic population urgently needs developing the regression equations for predicting spirometric parameters (SPs), which are specifically applicable to adipotic adults. Unfortunately, however, the reliable equations suitable for adipotic adults have not been reported to date. Recently, Yamaguchi et al have proposed the quantitative method to estimate the effects of adiposity on deciding the SPs incorporating with age-specific contributions of various explanatory, independent variables such as age (A), standing height (H), body weight (BW), and fat fraction of body mass (F). Extending the method proposed by Yamaguchi et al, we attempted to elaborate the novel regression equations applicable for diagnosing the spirometric abnormality in adipotic adults. For accomplishing this purpose, never-smoking, adipotic adults with body mass index (BMI) over 25 kg/m² and no respiratory illness were recruited from the general population in Japan (n = 3696, including men: 1890 and women: 1806). Introducing the four explanatory variables of A, H, BW, and F, gender-specific and age-dependent regression equations that allowed for prescribing the SPs in adipotic adults were constructed. Comparing the results obtained for non-adipotic adults (i.e., those with normal BMI), the negative or positive impact of height on SPs was preserved in adipotic adults, as well. However, the negative impact of age on SPs was blunted in adipotic men and the positive effect of BW on SPs was impeded in adipotic men and women. The fat fraction of body mass-elicited negative impact on SPs vanished in adipotic women. These results indicate that the regression equations of SPs for adipotic adults differ significantly from those for non-adipotic adults, leading to the conclusion that the regression equations for non-adipotic adults should not be used while judging the spirometric abnormalities in adipotic adults.

Key Words: Spirometric parameters, Reference mean, Lower limit of normal, Overweight, Obesity, Body weight, Fat fraction of body mass

Core tip: The impacts of age and a variety of anthropometric factors, including standing height, body weight, and fat fraction body mass, on decision of the spirometric parameters (SPs) differ significantly between non-adipotic adults [i.e., normal body mass index (BMI)] and adipotic adults (i.e., increased BMI). Therefore, if the reference means and lower limits of normal of SPs estimated from the regression equations established for non-adipotic adults are used, substantial errors will emerge while diagnosing the lung function abnormalities in adipotic adults.

INTRODUCTION

The prevalence of general population with adiposity, including overweight [25 kg/m² ≤ body mass index (BMI) < 30 kg/m²] and obesity (BMI ≥ 30 kg/m²), has markedly increased with time, reaching 37% in men and 38% in women over the world[1-3]. The proportion of adults with obesity significantly varies depending on the countries and regions ranging from more than 50% in Oceanian islands to 3%-7% in East Asia. The prevalence of adults with obesity has reached 32% in men and 34% in women in the United States, while 4.5% in men and 3.3% in women in Japan[3]. A remarkable increase in the prevalence of overweighing and obese subjects urgently needs developing the new tools specifically applicable to these subjects in a variety of medical disciplines, including the field of lung function testing. We defined the subjects with overweight or obesity as the “adipotic” subjects in the current editorial. In adipotic subjects, fat deposition in the thoracic or abdominal cavities limits the diaphragm mobility and rib movement, which results in that the lung volumes and the work of breathing are substantially impeded despite a lack of respiratory disease[4-11]. Fat deposition along large airways causes narrowing of central airways, leading to decreases in various lung function parameters such as forced vital capacity (FVC), forced expiratory volume during one second (FEV₁), and peak expiratory flow (PEF) rate. Meanwhile, fat accumulation along small airways elicits narrowing of peripheral airways, leading to decreases in flow parameters, including forced expiratory flow rate at 50% expiration of the FVC (FEF₅₀) and/or forced expiratory flow rate at 75% expiration of the FVC (FEF₇₅)[4,12,13]. Additionally, the adipose tissue acts as an endocrine or paracrine organ that produces bioactive mediators, which induces a proinflammatory state that causes immature development of the lung, bronchial hyperresponsiveness, increased risk of asthma, and so on[1].

Thyagarajan et al[14] demonstrated that subjects with overweight (BMI ≥ 26.4 kg/m²) had a reduction of 185 mL in the FVC and of 64 mL in the FEV₁ during a decade. Furthermore, they showed that the decrease in the FVC and FEV₁ was more prominent in obese individuals with BMI ≥ 30 kg/m². Saliman et al[15] showed that men and women with morbid obesity with BMI ≥ 40 kg/m² had, respectively, the FEV₁ of 65% and 79% of the reference means predicted from the classical regression equations for FEV₁. Rubinstein et al[12] demonstrated that even after normalizing the difference in slow vital capacity (VC), the FEF₇₅ was substantially low in men with obesity in comparison with that in men having normal BMI. The aforementioned facts suggest that if the abnormality of lung function is judged based on the reference means and lower limits of normal (LLNs) of spirometric parameters (SPs) obtained from the classical regression equations, the lung function of the adipotic subjects may frequently be judged to be abnormal even when they have no conspicuous respiratory illness. This is because the classical regression equations for SPs were developed based on the measures harvested predominantly from the subjects with no adiposity or from those with undefined adipotic states contaminated with no adiposity, overweight, and obesity. We consider that the regression equations for SPs with no thought about the excessive fat deposition in the body mislead physicians when judging the functional abnormalities in various lung diseases of adipotic individuals. In the current editorial, we set up the three purposes: (1) to survey the problems existing in the classical regression equations for SPs with little thought about adipotic states; (2) to demonstrate the regression equations for SPs in which the adipotic states are certainly taken into consideration using the data harvested from non-adipotic, never-smoking, healthy adults; and (3) to propose the novel regression equations for SPs with considerations of adipotic states, which are surely applicable for detecting the lung function abnormalities in adipotic adults.

Critical issues in classical regression equations for SPs with no consideration of adipotic states

Numerous ethnic-specific regression equations that allow for prescribing reference means and LLNs with regard to a variety of SPs in adults have been reported during half a century[16]. In essence, those regression equations were constructed by introduction of age and standing height as explanatory, independent variables. Applying the LMS strategy with smoothing function, in which the lambda (L), mu (M), and sigma (S) indicate the skewness, median, and dispersion of the measured data, respectively, Stanojevic et al[17] reported the valuable regression equations that are applicable to a wide age range including infants and elderly persons in white populations. Based on the work reported by Stanojevic et al[17], the Global Lungs Initiative (GLI), a Task Force of the European Respiratory Society (ERS), elaborated the global multi-ethnic regression equations that cover an almost entire range of age and are applicable to people of varied races[18-20]. The reason of why only the H was introduced as the explanatory anthropometric variable in the aforementioned regression equations is ascribed to the fact that the lung volume is modeled more appropriately by the height besides the age[18,19]. However, many studies conducted in the past confirmed that a variety of anthropometric variables other than H, including body weight (BW), BMI, body fat mass (BFM), and so on, also play an important role in deciding SPs [5,7,9,10,21-30]. Furthermore, we had better take notice of the fact that in previous studies, the effects of anthropometric variables, including H, BW, BMI, or BFM, on a certain spirometric parameter were presumed to be aging-independent. However, our recent studies[4,13] evidenced that H, BW, and BFM change with age.

The important roles of BW (or body mass) and BFM (body fat mass) on various SPs, which are closely linked to aging-dependent changes in BW and BFM, were extensively discussed in our previous papers[4,13]. Briefly, BW includes the respiratory muscles that modify a variety of pulmonary function parameters[5,7-10,31-33]. Irrespective of the gender, the muscle mass is significantly lost during a life with advancing age[34]. In addition, the muscle functions, including inspiratory and expiratory muscle strengths, are appreciably distorted as age advances[6,35,36]. The above-mentioned facts indicate that irrespective of the gender, the aging-dependent decrease in BW is primarily explained by the aging-dependent loss of muscle mass. However, the following fact should be noticed, i.e., the BFM that impairs various SPs[4,7,8,31] is included in the BW, as well, implying that BW acts as a double-edged sword in deciding SPs. Hence, the simultaneous introduction of BW and F (fat fraction of body mass) into the regression equations as the expiratory variables, in which F is the essential component forming BFM (BFM = BW•F), allows one to differentiate between the positive effect of BW and the negative effect of BFM on the decision of SPs in a first approximation[5,24,27].

Although many papers published so far used the BMI, body surface area, waist-hip index, abdominal circumference, or thoracic circumference as explanatory variables for SP predictions[5,9,10,21,22,29,30], the effects of these variables on SPs are explicable from the combined effects of A, H, BW, and F[4,13].

Regression equations for SPs with considerations of adipotic states elaborated from measures of non-adipotic adults

Based on the above-mentioned facts, Yamaguchi et al[4,13] performed semi-quantitative and quantitative studies under the following considerations: (1) SPs generally receive the influence of a variety of anthropometric variables represented by H, BW, and F; (2) their effect is age-specific; and (3) the extent of their age-dependent contribution is gender-specific. The study of Yamaguchi et al[13] was conducted on a large number of healthy, Japanese adults (≥ 20 years) with never-smoking and BMI < 30 kg/m², who were selected among individuals in the general population in Japan (n = 9839, including 3056 males and 6783 females). According to the international classification of BMI recommended by the World Health Organization (WHO)[37], individuals with no adiposity were defined as those with BMI < 25 kg/m², overweighing individuals as those with 25 kg/m² ≤ BMI < 30 kg/m², while obese individuals as those with BMI ≥ 30 kg/m². The individuals who meet the criteria of either overweight or obesity were defined as adipotic individuals (BMI ≥ 25 kg/m²). The regression equations elaborated by Yamaguchi et al[13] were constructed based on the SP data harvested from never-smoking, healthy adults with BMI < 30 kg/m². In a strict sense, the participants recruited for their study were non-obese subjects, in whom the overweighing subjects (25 kg/m² ≤ BMI < 30 kg/m²) were included to some extent. However, the percentage of overweighing subjects was low; i.e., 6.5% for men and 7.3% for women, which indicates that it may be allowed to presume that the regression equations developed from the above subjects are the non-adipotic equations in an initial approximation.

The logarithmic (Ln), additive model, in which age (A), standing height (H), BW, and fat fraction of body mass (F) are taken as explanatory variables in predicting a specific SP, is given by:

Ln(SP) = a₀ + a₁•Ln(A) + a₂•Ln(H) + a₃•Ln(BW) + a₄•Ln(F) ······ eq. (1)

In the eq. (1), the a_i (i is 1, 2, 3, or 4) assumes the age-dependent and/or age-independent coefficient concerning the partial regression of a certain explanatory variable, while the a₀ is the constant. The age-dependent variation of the a_i is approximated by the linear function as[13]:

a_i = b_i + c_i•A ······ eq. (2)

where the b_i (i is 1, 2, 3, or 4) and the c_i (i is 1, 2, 3, or 4) are the constants. The coefficients of a₀, b_i (i is 1, 2, 3, or 4), and c_i (i is 1, 2, 3, or 4) in males and females for the six spriometric parameters (SPs) (FVC, FEV₁, FEV₁/FVC, PEF, FEF₅₀, and FEF₇₅) are determined by applying the multiple-regression analysis in collaboration with least-squares minimization. The lower limit of normal (LLN) of respective Ln (SP) is decided according to the fifth percentile of the distribution of residuals between measured and predicted values. The gap between the Ln(reference mean) and the fifth percentile of the residual’s distribution is defined as ΔLLN. Therefore, the LLN for a specific SP is provided as follows:

LLN = (reference mean)•Exp[-ΔLLN] ······ eq. (3)

where Exp indicates the exponential function. Using the ΔLLN, the coefficient of variation (CV) for each SP is given by:

CV = 100•[Exp(ΔLLN) - 1] ······ eq. (4)

The a_i values (i is 0, 1, 2, 3, or 4) and ΔLLN thus determined are depicted in Table 1, in which A, M, and F indicate age (years), male subjects, and female subjects, respectively. The reference mean and LLN of a specific SP can be calculated using the eq. (1) and the eq. (3), respectively.

Table 1 Partial regression coefficients for spirometric parameters of non-adipotic subjects[13].

Spirometric parameter	a0	a1	a2	a3	a4	ΔLLN
Ln (FVC)
M	-10.269	0.358	1.989	0.164 - 0.003•A	-0.001•A	0.146
F	-5.659	-0.009•A	0.909 + 0.013•A	0.497 - 0.007•A	-0.067	0.178
Ln (FEV1)
M	-7.823	0.116 - 0.002• A	1.74	0	-0.001•A	0.136
F	-5.784	-0.003 •A	1.291	0.082 + 0.002 × A	-0.002•A	0.17
Ln (FEV1/FVC)
M	6.041	-0.11	-0.238	0	0	0.075
F	6.313	-0.178	-0.289	0.001×A	-0.171 + 0.003•A	0.079
Ln (PEF)
M	-1.185	-0.011•A	0.573 + 0.010•A	0	0	0.246
F	0.078	-0.012•A	0.011•A	0.293	-0.002•A	0.284
Ln (FEF50)
M	-1.194	-0.002•A	0.462	0.14	0	0.314
F	1.238	-0.004•A	-0.005•A	0.009•A	-0.15	0.37
Ln (FEF75)
M	-6.334	-0.003•A	1.498	-0.171	-0.282 + 0.004•A	0.4
F	-0.057	-0.88	0.381	0.167 + 0.002•A	-0.869 + 0.012•A	0.576

a₀ is invariable constant, while a₁, a₂, a₃, and a₄ are, respectively, age-dependent and/or age-independent partial regression coefficient for describing the effect of age (A), height (H), body weight (BW), and fat fraction of body mass (F) on a specific spirometric parameter (SP). Using a_i (i = 0 to 4), reference mean of each Ln (SP) is estimated (see eq. (1)); ΔLLN: The 5^th percentile of the residual’s distribution of each Ln (SP), from which lower limit of normal (LLN) of each SP is determined [see eq. (3)]. M: Male; F: Female; A: Age; FVC: Forced vital capacity (L); FEV₁: Forced expiratory volume after one second (L); PEF: Peak expiratory flow rate (L/s); FEF₅₀: Forced expiratory flow rate at 50% expiration of FVC (L/s); FEF₇₅: Forced expiratory flow rate at 75% expiration of FVC (L/s).

When constructing the regression formula predicting a specific spirometric measure, the best statistic procedure may be the application of the LMS method that the GLI proposed[17-20,38]. In the LMS method, the Lambda (L) indicates the skewness induced by the gap of the variables, including the objective variables, explanatory variables, and residuals, from the normality. The Mu (M) indicates the variation in the median of an objective outcome, whereas the Sigma (S) expresses the scattering of measured values centered on the reference mean[17-20,38,39]. These facts suggest that the LMS method can be applied for any data set that does not follow the normal distribution. On the other hand, the application of the statistical strategy such as the multiple regression analysis with least-squares minimization requires the establishment of normal distributions in the objective variable, explanatory variables, and residuals. Of them, the confirmation of normal distribution regarding the residual is the minimum requirement when the least-squares minimization is applied[40]. The significance of Mu and Sigma can be estimated from the reference mean and the coefficient of variation, respectively. Although the significance of lambda cannot be rectified in the least-squares minimization, Yamaguchi et al[13] demonstrated that the residuals of the FVC, FEV₁, and FEV₁/FVC (i.e., the major SPs) are approximated by the normal distributions in both genders, whereas the residuals of the flow parameters, especially the female FEF₇₅, are appreciably disengaged from the normal distributions. Supporting the findings reported by Yamaguchi et al[13], Kubuta et al[41] indeed found that the reference means and LLNs of major SPs (FVC, FEV₁, and FEV₁/FVC) estimated from the LMS method differ minimally from those from the multiple regression analysis with least-squares minimization. Hence, Yamaguchi et al[13] concluded that the regression equations predicting the major SPs, which are elaborated applying the least-squares minimization, are not inferior to those established on the basis of the LMS strategy.

The qualitative features obtained from the non-adipotic regression equations are summarized as follows[13]: (1) the SPs are negatively influenced by age and fat fraction of body mass while positively influenced by height and BW in an age-dependent and/or age-independent fashion; (2) significant errors concerning the reference mean and LLN of a specific SP are manifest when disregarding the age-dependent and/or age-independent effects of BW and fat fraction of body mass; and (3) the age-dependent and/or age-independent effects of explanatory variables on SPs are distinctly gender-specific; the gender-specific contributions of BW and fat fraction of body mass are of importance, particularly for prescribing the female SPs.

Regression equations for SPs with considerations of adipotic states elaborated from measures of adipotic adults

Extending the study of Yamaguchi et al[13], we try to establish the novel regression equations that incorporate with age-specific contributions of age (A), standing height (H), BW, and fat fraction of body mass (F) in determining a variety of SPs (FVC, FEV₁, FEV₁/FVC, PEF, FEF₅₀, and FEF₇₅), based on the spirometric measures harvested from never-smoking, adipotic adults (BMI ≥ 25 kg/m²) with no conspicuous respiratory illness (n = 3696, including men: 1890 and women: 1806). These subjects were defined as cohort A (Figure 1). The partial regression coefficients of a₀, b_i (i is 1, 2, 3, or 4), and c_i (i is 1, 2, 3, or 4) in the eq. (1) and in the eq. (2) for six SPs predicting the reference means and LLNs for adipotic men and women are denoted in Table 2.

Figure 1 Distributions of measured forced vital capacity and forced expiratory volume after one second along age axis in cohort A. A: Forced vital capacity (FVC) in men; B: Forced expiratory volume after one second (FEV₁) in men; C: FVC in women; D: FEV₁ in women.

Table 2 Partial regression coefficients for spirometric parameters of adipotic subjects (cohort A).

Spirometric parameter	a0	a1	a2	a3	a4	ΔLLN
Ln (FVC)
M	-7.158	0	1.669	-0.001•A	-0.1	0.375
F	-7.752	0	1.793	-0.001•A	0	0.279
Ln (FEV1)
M	-5.593	-0.001•A	1.321	0	-0.124	0.379
F	-6.439	-0.001•A	1.495	0	0	0.287
Ln (FEV1/FVC)
M	5.509	0	-0.2	0	0	0.11
F	5.661	0	-0.272	0.044	0	0.111
Ln (PEF)
M	-2.597	0	0.936	-0.001•A	-0.001•A	0.484
F	-1.859	-0.010•A	0.649 + 0.009•A	0	0	0.391
Ln (FEF50)
M	0.665	0	0	0.002•A	-0.855 + 0.014•A	0.566
F	0.779	-0.015•A	0.014•A	0	0	0.557
Ln (FEF75)
M	-1.217	0	0	0.216	-0.914 + 0.013•A	0.739
F	-2.927	-0.003•A	0.676	0	0	0.701

a₀ is invariable constant, while a₁, a₂, a₃, and a₄ are, respectively, age-dependent and/or age-independent partial regression coefficient for describing the effect of age (A), height (H), body weight (BW), and fat fraction of body mass (F) on a specific spirometric parameter (SP). Using a_i (i = 0 to 4), reference mean of each Ln (SP) is estimated (see eq. (1)); ΔLLN: The 5^th percentile of the residual’s distribution of each Ln (SP), from which lower limit of normal (LLN) of each SP is determined [see eq. (3)]. M: Male; F: Female; A: Age; FVC: Forced vital capacity (L); FEV₁: Forced expiratory volume after one second (L); PEF: Peak expiratory flow rate (L/s); FEF₅₀: Forced expiratory flow rate at 50% expiration of FVC (L/s); FEF₇₅: Forced expiratory flow rate at 75% expiration of FVC (L/s).

To learn the validity of the regression equations elaborated from the SP data measured for cohort A, the never-smoking, obese subjects with BMI ≥ 30 kg/m² and no respiratory illness were separately recruited and defined as cohort B (n = 500 including men: 231 and women: 269).

Effects of age (A) on SPs of adipotic adults: In adipotic men, the partial regression coefficients (a₁) of the Ln(A) for the SPs, with the exception of FEV₁, were zero, which indicates that most of the SPs are insensitive to aging in adipotic men; namely, in a sharp contrast to non-adipotic men[13], a fundamental role of aging in decreasing SPs was blunted in adipotic men. The a₁ in adipotic women exerted a negative (decreasing) impact on many SPs, including FEV₁, PEF, FEF₅₀, and FEF₇₅, in an age-dependent manner, which is qualitatively similar to that investigated for non-adipotic women[13]. Collectively, the effect of aging on the decision of SPs in adipotic adults is highly gender-specific.

Effects of height (H) on SPs of adipotic adults: In general, H acted as the factor augmenting the major SPs, including FVC and FEV₁, in an age-independent manner irrespective of the gender. However, the FEV₁/FVC decreased with increasing H in an age-independent manner in both genders. The male FEF₅₀ and FEF₇₅ were not influenced by the change in H. These findings are qualitatively consistent with those investigated for non-adipotic men and women[13], which suggests that the positive and/or negative contributions of height on SPs are preserved in adipotic adults, as well.

Effects of BW on SPs of adipotic adults: In men, the age-dependent, negative contribution of a₃ [partial regression coefficient of the Ln (BW)] was found to be significant for deciding the FVC and PEF, whereas the age-dependent, positive contribution of a₃ was identified to be important for deciding the FEF₅₀ and the age-independent, positive contribution of a₃ for deciding the FEF₇₅. However, the FEV₁ and FEV₁/FVC were insensitive to the change in BW. In women, the situation was qualitatively different from men; namely, the FVC was negatively associated with the change in BW in an age-dependent manner, while the FEV₁/FVC was positively associated with the change in BW in an age-independent manner. Other SPs in women were not influenced by the change in BW. These findings indicate that the effect of BW on the decision of SPs qualitatively differs between non-adipotic adults and adipotic adults.

Effects of fat fraction of body mass (F) on SPs of adipotic adults: In men, F exerted a negative impact on the PEF in an age-dependent manner while lowering the FVC and FEV₁ in an age-independent manner. On the other hand, the negative effect of F was faded as age advanced in the FEF₅₀ and FEF₇₅ in men. To our astonishment, the a₄ values [the partial regression coefficients of Ln(F)] were zero for all SPs in women, which indicates no effect of F on any SP in the adipotic women. This differs strikingly from the findings observed for non-adipotic women, in whom F exerted a negative impact on all SPs in an age-dependent or age-independent manner[13]. These findings are indeed unexpected, on which we have no convincing explanation. However, the following mechanisms may plausibly explain them; i.e., the F measured with the classical bioelectrical impedance method detects the overall fat accumulation in the body, including subcutaneous and visceral fats. A large quantity of subcutaneous fat in adipotic women may conceal the ability of the overall fat fraction to detect the change in fat deposition in the visceral tissues and organs, including thoracic and abdominal cavities, suggesting that the sensitivity of the overall fat fraction to detecting the fat deposition in the thoracic and abdominal cavities is relatively high in non-adipotic women but relatively low in adipotic women.

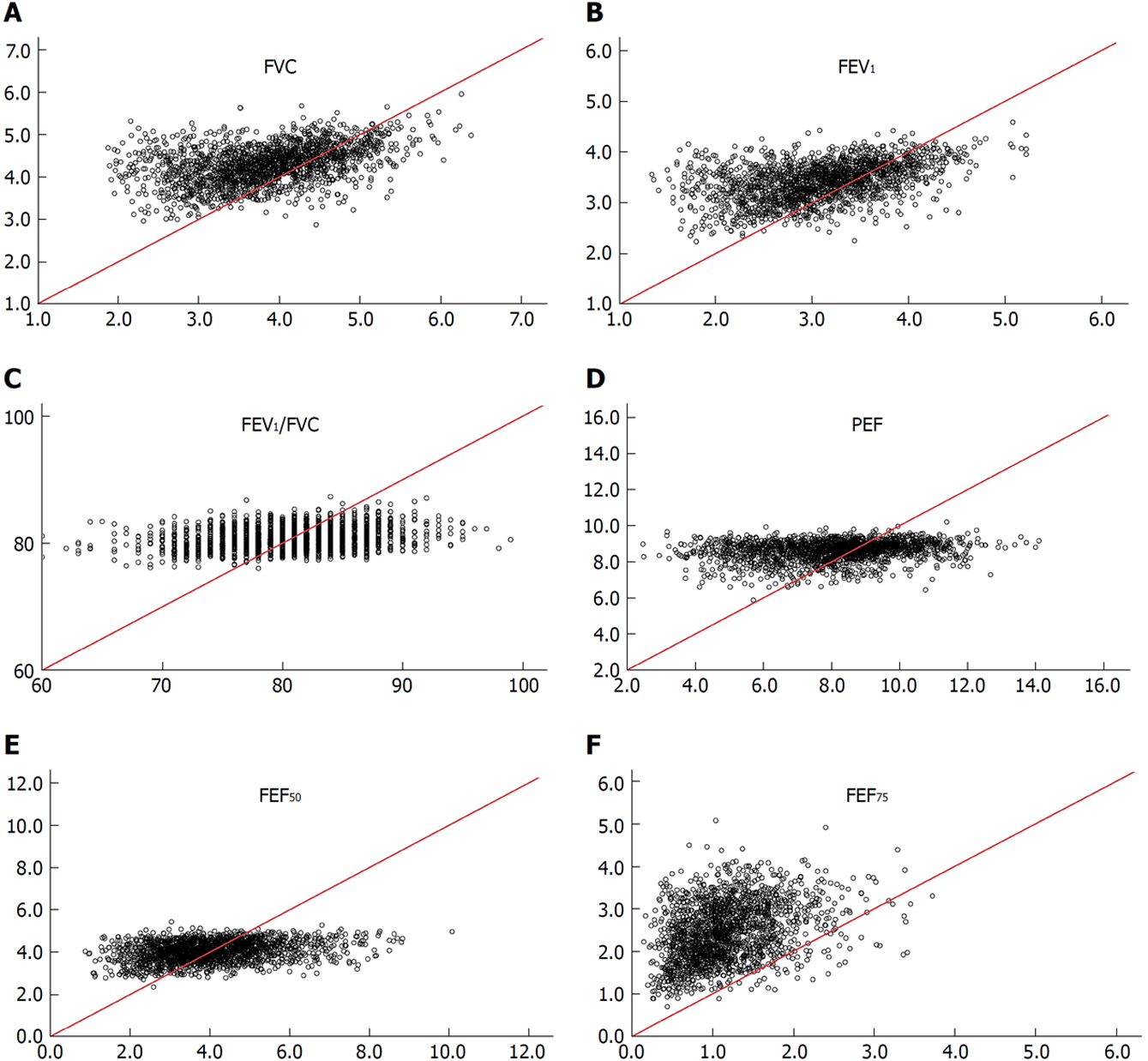
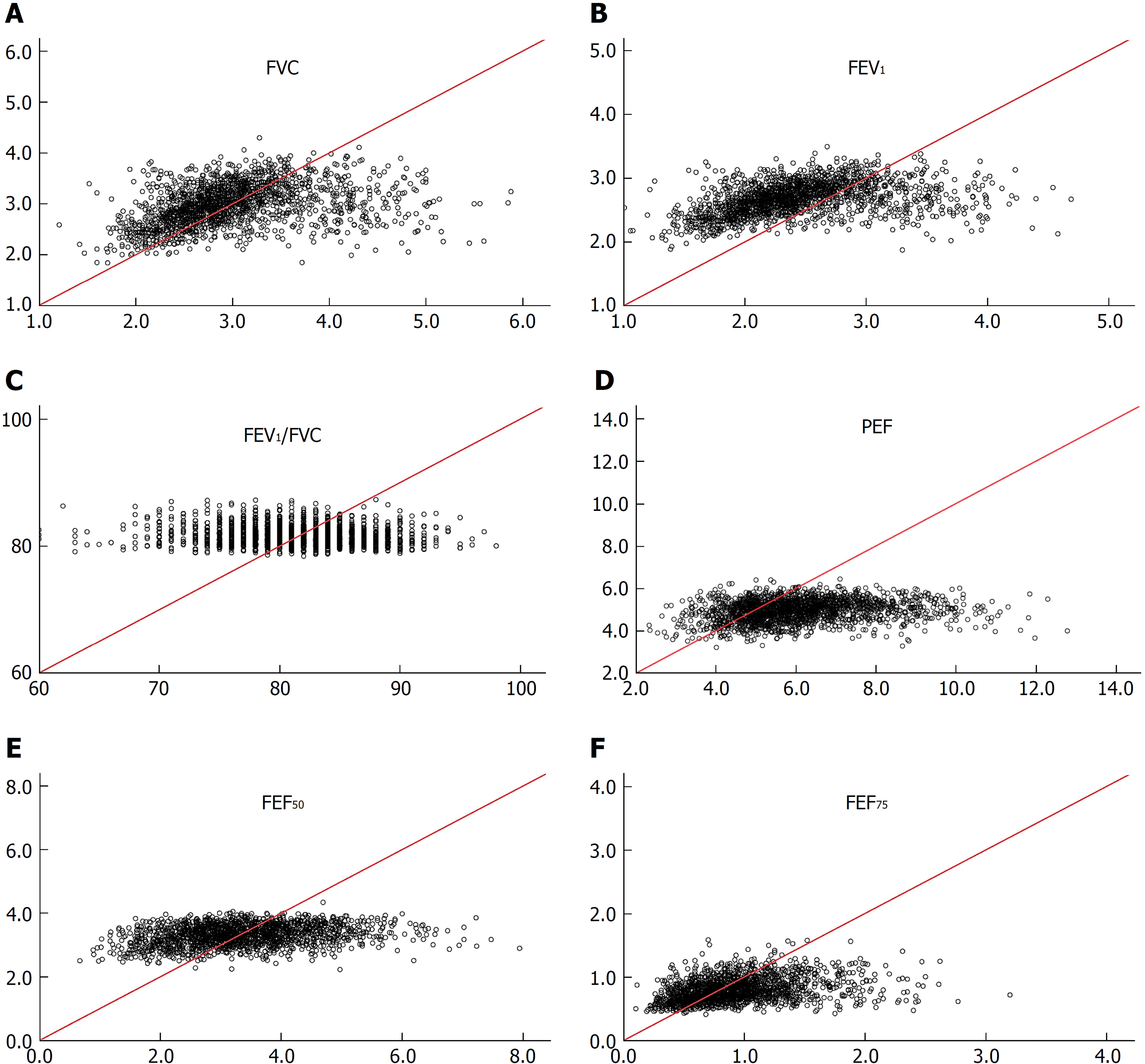
Regression equations of SPs established for non-adipotic adults are not applicable to diagnosing spirometric abnormalities in adipotic adults: Irrespective of the gender, the non-adipotic regression equation[13] could not predict any SP measure obtained from adipotic adults (Figures 2 and 3). To confirm this issue further, the incidence of obese subjects (cohort B, recruited apart from cohort A) who are judged to have impaired lung function was evaluated under the two conditions. The analytical results are shown in Table 3, in which (1) indicates the judgement based on LLNs from regression equations constructed from SP data of adipotic subjects; and (2) indicates the judgement based on LLNs from regression equations constructed from SP data of non-adipotic subjects. On average, 3.8% of the subjects (1.2% in obese men and 6.3% in obese women) in cohort B were judged to have impaired lung function when the LLNs obtained from the adipotic equations were used, whereas 20.2% of the subjects (22.3% in obese men and 20.0% in obese women) in cohort B were judged to have impaired lung function when the LLNs estimated from the non-adipotic equations were used. These facts suggest that about one-fifth of obese subjects with no conspicuous respiratory illness are judged to be abnormal in lung function (i.e., false positive) when the LLNs of non-adipotic equations are applied. Furthermore, we should give a considerable attention to the fact that the false-positive percentage of FVC or FEV₁ in obese subjects is substantially high if the LLNs obtained from the non-adipotic equations are used; that is, 24.8% for male FVC, 26.1% for male FEV₁, 24.1% for female FVC, and 47.8% for female FEV₁. These results indicate that since the FVC and FEV₁ are the major SPs for judging the abnormality in lung function[42], a large error as to a clinical decision-making may be produced in obese subjects if the LLN for FVC or FEV₁ estimated from the non-adipotic equations is applied.

Figure 2 Comparison of measured spirometric parameters of men in cohort A and reference means calculated from regression equations constructed for non-adipotic men. Horizontal axis: Measured values; Vertical axis: Values predicted from the non-adipotic regression equation[13]; Red line: Line on identity. FVC: Forced vital capacity; PEF: Peak expiratory flow; FEV₁: Forced expiratory volume after one second.

Table 3 Incidence of obese subjects (cohort B) who are judged to have impaired lung function.

	Measured values < LLNs of adipotic equations	Measured values < LLNs of non-adipotic equations
FVC
M	0.40%	24.8%b
F	6.20%	24.1%b
FEV1
M	0.40%	26.1%b
F	8.40%	47.8%b
FEV1/FVC
M	3.10%	16.8%b
F	2.20%	6.6%d
PEF
M	1.30%	26.5%b
F	3.60%	19.3%b
FEF50
M	0.90%	27.9%b
F	11.70%	16.40%
FEF75
M	1.30%	11.5%b
F	5.50%	6.60%

^bP < 0.0001.

^dP < 0.02 between the two conditions (the χ² test). LLNs of respective SPs are estimated from the 5^th percentiles of the residual’s distributions applying eq. (3) to adipotic and non-adipotic regression equations. M: Male; F: Female; A: Age; FVC: Forced vital capacity (L); FEV1: Forced expiratory volume after one second (L); PEF: Peak expiratory flow rate (L/s); FEF₅₀: Forced expiratory flow rate at 50% expiration of FVC (L/s); FEF₇₅: Forced expiratory flow rate at 75% expiration of FVC (L/s).

Figure 3 Comparison of measured spirometric parameters of women in cohort A and reference means calculated from regression equations constructed for non-adipotic women. Horizontal axis: Measured values; Vertical axis: Values predicted from the non-adipotic regression equation[13]; Red line: Line on identity. FVC: Forced vital capacity; PEF: Peak expiratory flow; FEV₁: Forced expiratory volume after one second.

CONCLUSION

In the present editorial, we identified that the regression equations of SPs for adipotic adults differ significantly from those for non-adipotic adults. Therefore, the regression equations elaborated for non-adipotic adults should not be used while judging the lung function abnormalities in adipotic adults.