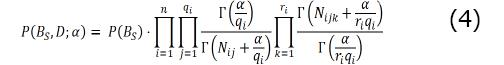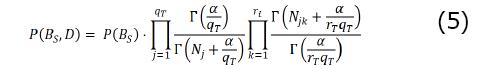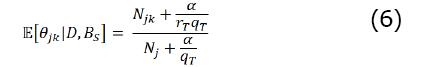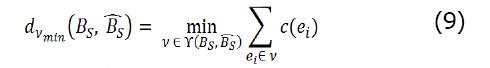Published online Sep 14, 2018. doi: 10.5306/wjco.v9.i5.98
Peer-review started: April 27, 2018
First decision: July 9, 2018
Revised: July 24, 2018
Accepted: August 5, 2018
Article in press: August 5, 2018
Published online: September 14, 2018
Processing time: 140 Days and 15.9 Hours
To develop a framework to incorporate background domain knowledge into classification rule learning for knowledge discovery in biomedicine.
Bayesian rule learning (BRL) is a rule-based classifier that uses a greedy best-first search over a space of Bayesian belief-networks (BN) to find the optimal BN to explain the input dataset, and then infers classification rules from this BN. BRL uses a Bayesian score to evaluate the quality of BNs. In this paper, we extended the Bayesian score to include informative structure priors, which encodes our prior domain knowledge about the dataset. We call this extension of BRL as BRLp. The structure prior has a λ hyperparameter that allows the user to tune the degree of incorporation of the prior knowledge in the model learning process. We studied the effect of λ on model learning using a simulated dataset and a real-world lung cancer prognostic biomarker dataset, by measuring the degree of incorporation of our specified prior knowledge. We also monitored its effect on the model predictive performance. Finally, we compared BRLp to other state-of-the-art classifiers commonly used in biomedicine.
We evaluated the degree of incorporation of prior knowledge into BRLp, with simulated data by measuring the Graph Edit Distance between the true data-generating model and the model learned by BRLp. We specified the true model using informative structure priors. We observed that by increasing the value of λ we were able to increase the influence of the specified structure priors on model learning. A large value of λ of BRLp caused it to return the true model. This also led to a gain in predictive performance measured by area under the receiver operator characteristic curve (AUC). We then obtained a publicly available real-world lung cancer prognostic biomarker dataset and specified a known biomarker from literature [the epidermal growth factor receptor (EGFR) gene]. We again observed that larger values of λ led to an increased incorporation of EGFR into the final BRLp model. This relevant background knowledge also led to a gain in AUC.
BRLp enables tunable structure priors to be incorporated during Bayesian classification rule learning that integrates data and knowledge as demonstrated using lung cancer biomarker data.
Core tip: Bayesian rule learning is a unique rule learning algorithm that infers rule models from searched Bayesian networks. We extended it to allow the incorporation of prior domain knowledge using a mathematically robust Bayesian framework with structure priors. The hyperparameter of the structure priors enables the user to control the influence of their specified prior knowledge. This opens up many possibilities including incorporating uncertain knowledge that can interact with data accordingly during inference.
- Citation: Balasubramanian JB, Gopalakrishnan V. Tunable structure priors for Bayesian rule learning for knowledge integrated biomarker discovery. World J Clin Oncol 2018; 9(5): 98-109
- URL: https://www.wjgnet.com/2218-4333/full/v9/i5/98.htm
- DOI: https://dx.doi.org/10.5306/wjco.v9.i5.98
Knowledge discovery from databases (KDD) is the non-trivial extraction of valid novel, potentially useful, and understandable patterns from the dataset[1]. Data mining is the computational process of the extraction of these patterns. In biomedicine, data mining is extensively applied for knowledge discovery[2]. The recent advances in biomedical research, triggering an explosion of data, have encouraged these applications. Particularly, the development of high-throughput “omic” technologies has generated a large number of datasets, which provide a holistic view of a biological process. These datasets present opportunities to discover new knowledge in the domain. They also present some challenges, especially from their high-dimensionality. High-dimensional datasets are challenging to data mining algorithms because several thousands of candidate variables (e.g., gene expressions or SNPs) can potentially explain an outcome variable of interest (e.g., phenotypes or disease states) but have only a few instances as evidence to support an explanation. These large numbers of candidate variables generate a model search space that is very large for data mining algorithms to explore efficiently, and having only a few instances generates uncertainty for the algorithm to determine the correctness of any candidate model. In such model search spaces, data mining algorithms can easily get stuck in local optima or they may infer associations between spurious variables and the outcome variable, by chance.
Fayyad et al[3], emphasized the importance of domain prior knowledge in all steps of the KDD process. In biomedicine, often in addition to the dataset, we have some prior domain knowledge about the dataset. This domain knowledge can help guide the data mining algorithm to focus on regions in the model search space that are either objectively more promising for a given problem or subjectively more interesting to a user. The prior knowledge can come from domain literature (e.g., searching through PubMed), a domain expert (e.g., a physician), domain knowledge-bases (e.g., Gene Ontology) or from other related datasets [e.g., from public data repositories like Gene Expression Omnibus (GEO)]. It is now imperative to develop data mining methods that can leverage domain knowledge to assist with the data mining process.
Rule learning methods are among the oldest, well-developed, and widely applied methods in machine learning. They are particularly attractive for KDD tasks because they generate interpretable models with understandable patterns and have good predictive performance. Interpretable models are succinct, human-readable models that explain the reasoning behind their predictions. Bayesian rule learning (BRL) is a rule learning method that has been shown to perform better than state-of-the-art interpretable classifiers on high-dimensional biomedical datasets[4,5]. BRL takes a dataset as input and searches over a space of Bayesian belief-networks (BN) to identify the BN that best explains the input dataset. BRL then infers a rule model from this BN. BRL uses the Bayesian score[6] as a heuristic to evaluate a BN during search. The score allows the user to specify a prior belief distribution over the space of BNs that encodes our prior beliefs about which models are more likely to be correct than others with respect to our domain knowledge. Typically in literature uninformative priors are used, which means that we claim that a priori all models are equally likely to be correct. As we saw earlier, often along with the dataset, additional domain knowledge is available that can assist with the data mining process. These sources lead us to believe that some models are more likely to be correct than others even before we see the dataset. We can specify this belief using informative priors. Two approaches to using informative priors in literature have shown promise[7,8]. In the Methods and Materials section of this paper, we discuss each of the two approaches and describe ways to extend BRL to specify such informative priors that can incorporate domain knowledge.
In this paper, we implemented an approach to incorporate prior domain knowledge into the BRL learning process using informative priors. We evaluated the effect of this prior knowledge on model learning using experiments with simulated and a real-world lung cancer prognostic dataset.
In this section, we describe our implementation in BRL to incorporate prior domain knowledge, and then describe two experiments we conducted to evaluate this implementation. Specifically, we describe a BRL greedy best-first search algorithm, the heuristic score used by the search to evaluate candidate models, and our approach to extend this heuristic score to incorporate prior background domain knowledge using informative priors. We call this extension to BRL as BRLp (BRL with informative priors). After describing our implementation of BRLp, we describe two experiments we conducted to study the effects of informative priors in model learning: (1) using simulated data; and (2) on a real-world lung cancer prognostic dataset.
BRL is a rule-based classifier that takes as input, a dataset D, and returns a rule set model. Let the dataset D be an observed instantiation of a system with a probability distribution over a set of n random variables and a target random variable of interest,D = {Xi,Ti; i ∈ 1...n} . Here, T is the target variable of interest, which is the dependent variable for the prediction task. Every other variable, Xi in D is an independent random variable that may help predict T. There are a total of m instances in D. In the classification problem, our task is to accurately predict the value of the target variable. For example, consider a diagnostic problem of predicting a disease outcome for a patient, say lung cancer outcome (either Case or Normal), using gene expression biomarker data, measured for each patient. Here, the dataset D would be composed of a set of m patients, each with n gene expression measurements {Xi; i ∈ 1...n}. The target variable T is the binary-valued lung cancer outcome variable, T = {Case, Normal}, for each patient in the dataset.
The BRL search algorithm explores a space of BNs, learned from the observed dataset D, and returns the most optimal BN found during the search. A BN is a graphical representation of the probabilistic dependencies of the different variables in the system under study. They are represented as a directed acyclic graph (DAG). In our lung cancer diagnostic problem example, an example of probabilistic dependence could be some hypothetical gene expression, say the binary-valued XA = {Up; Down} with a value for up-regulated and a value for down-regulated gene A, is known to be predictive of the outcome T. Then an optimal BN should contain a directed edge from XA→T. In other words, the lung cancer outcome depends upon whether or not gene XA is expressed. In such a BN, the probability distribution, P (T | XA) is the parameter of the BN.
The parameters of the BN can be represented in form of a conditional probability table (CPT). The CPT is often stored in form of decision trees[9,10]. The BRL generates a mutually exclusive and exhaustive set of inference rules from this decision tree for prediction of class of any new test instances. Here, each path from root to leaf of the decision tree is interpreted as a rule. The BRL rules are represented in the form of explicit propositional logic: IF antecedent THEN consequent. The rule antecedent is the condition made up of conjunctions (ANDing) of the independent random variable-value pairs, which when matched to a test instance, implies the rule consequent composed of the dependent target variable-value. Continuing with our example, a learned rule can be IF (XA = Up) THEN (T = Case). In other words, if the gene XA is up-regulated then the patient is classified to have a lung cancer outcome as a Case. There are several types of BRL search algorithms[4,5,11] to help find the optimal BN. In this paper, we will only discuss a simple greedy best-first search algorithm from our previous work[4] and is summarized in the next sub-section.
BRL greedy best-first search algorithm: The BRL greedy best-first search algorithm is described in detail in the paper by Gopalakrishnan et al[4], where it is referred to as BRL1. In this paper, we will refer to this algorithm simply as BRL. We will summarize the algorithm in this subsection. The BRL algorithm initializes the search with a network structure with just the variable T and no parent nodes. In each iteration of the algorithm, one new parent is added to T among the n random variables that is not already a parent of T. This BN implies the hypothesis that T is dependent upon the set of variables added as parents to T. This process is called model specialization. The resulting models from that iteration is added to a priority queue. The priority queue sorts these specialized models by evaluating them using a heuristic score called the Bayesian score, which evaluates the likelihood that the observed dataset was generated by a given hypothesized BN model. This score is described in detail in the next subsection. The greedy search picks the model in the head of the priority queue at the end of the iteration. This model is evaluated to be the best scoring model among the specializations in that iteration. In the next iteration, this model is selected for further specialization by adding more parents. The search terminates when a subsequent specialization step fails to improve the heuristic score. The search also terminates if the model has reached a limit on the maximum number of parents allowed for T. This search parameter is called maximum conjuncts. Finally, BRL generates a rule model inferred from the model returned by the search.
BRL heuristic score (Bayesian score): BRL search evaluates the quality of a candidate BN model using a heuristic score called the Bayesian score[9]. In this sub-section, we describe this score. We represent a BN model as the tuple B = (BS, BP), where BS is the network structure with a subset of π discrete-valued nodes, and BP is the numerical parameters of the network. The posterior probability of the candidate structure given the observed dataset, D, is calculated as in Equation 1.
P (BS | D) = P (BS, D)/P (D) (1)
Since we are comparing Bayesian networks learned from the same dataset D, the denominator does not affect our decision. Only the numerator helps with model selection as shown in Equation 2.
P (BS | D) ∝ P (BS, D) (2)
The joint probability of the network structure and the observed dataset, P (BS, D), is equal to the prior probability of the network structure, P (BS) and the likelihood that the observed data was generated by that network structure,P (D | BS) . This is shown in Equation 3.
P (BS, D) = P (BS) · P (D | BS) (3)
To compute the joint probability of the network structure and the observed dataset, P (BS, D), we use the BDeu score[6]. We get Equation 4.
Here, i iterates through each node in the BN with n nodes. Index j iterates though all, qi, possible variable-value instantiations of the parents of the ith node. Index k iterates through all ri values of the ith node. Nijk is the number of instances in D, where the variable i takes the kth value and its parent variables take the ith variable-value instantiation, and Nijk = ΣkNijk. The Gamma function is defined as Γ(x) = (x-1) !. The α is a user-defined parameter called prior equivalent sample size (pess). We set α = 1, which allows the data to easily dominate the score[9]. The P (BS) term is called the structure prior (see[9] section 18.3.6.1 for details) that represents the prior belief distribution over all network structures before we look at the data. The remaining terms in Equation 4 compose the likelihood term that infers the likelihood of the network from the observed data.
In the classification task using BRL, we do not learn a fully generalized BN but only care about the relationship of the variables with a specific target variable of interest, T. Variable T is discrete with different values. The set of parents of the ith variable is represented as πi. In BRL, we learn a constrained BN with node T and its set of parents, πT. The set πi can have qT possible attribute-value instantiations. So, for BN search in BRL, we optimize the heuristic score in Equation 5.
The expectation of each parameter value of the BN is computed with Equation 6.
We use this value as the posterior probability of the rule. The number of rules inferred by BRL is equal to the number of θjk values in the BN. The expectation of this value shows the degree of support a rule has in the observed dataset.
BRL with structure priors: In Equation 5, the P (BS) term is the structure prior that represents the prior distribution over all network structures. Here, we can specify our prior bias of certain network structure over others to skew the BRL search to focus on certain network structures more than others. Typically, in literature uninformative priors are used, which means that a priori we claim that we do not have any preference of network structures over the others. BRL in this case lets the data alone decide the final learned model. The challenge of specifying these priors is that the total number of network structures grows super-exponentially with the number of variables n[12]. It often becomes infeasible to specify structure priors for each of these network structures for even moderately sized datasets. So far in BRL, we had been using an uninformative prior by setting P (BS) = 1, in Equation 5.
Castelo and Siebes[7] describe a promising approach to elicit structure priors by specifying the probability of the presence or absence of each edge in the network structure. The user only needs to specify the probability of a subset of edges in the network structure. The probabilities for all the remaining edges are assigned a discrete uniform distribution value. A challenge using this approach is to specify the values of these probabilities. In our experiments with BRL using these priors, we observed that the likelihood term in Equation 5 always dominates the structure prior term. It would help us if we could control the influence of structure priors over the likelihood term using a scaling factor. As we described earlier in the introduction section, the background knowledge, we specify, itself has uncertainty associated with it. A scaling factor would help us control the influence of data and our prior knowledge.
Mukherjee and Speed[8] propose an informative prior that uses a log-linear combination of weighted real-valued function of the network structure, fi (BS). This function is called the concordance function. It can be any function that monotonically increases with the increase in agreement between the learned network structure and the prior beliefs of the user. This is shown in Equation 7.
P (BS) ∝ exp [λ· Σwifi (BS) ] (7)
The hyperparameter wi are the positive weights that represent the relative importance of each function. The hyperparameter λ is a scaling factor that helps to control the overall influence of the structure prior. This will help us quantify the uncertainty in the validity of our prior knowledge.
The structure prior we used for BRLp comes from an instantiation of the general form of this prior, shown in Equation 7, as described by Mukherjee and Speed[8]. It allows the user to specify their prior beliefs about the presence and absence of the edges in the network structure. This instantiation is shown in Equation 8.
P (BS) ∝ exp [λ· (|E (BS) ∩ E+| - |E (BS) ∩ E-|) ] (8)
Here, set E+ (positive edge-set) represents the set of edges the user believes should be present in the model, and set E- (negative edge set) represents the set of edges the user believes should be absent from the model. So, the concordance function in this instantiation simply gives a positive count for if the candidate graph contains an edge from the positive edge-set, and a negative count (penalty) when it contains an edge from the negative edge-set. In this instantiation, the weights hyperparameter is set to 1, since our counts are all valued 1. We need to learn the value of the hyperparameter λ. The range of values it can take depends upon the well-known Jeffrey’s scale[13]. When λ = 0, the whole exponent becomes 0, and P (BS) = exp (0) = 1, which is the uninformative prior. In other words, when λ = 0, BRLp should have no effect of structure prior and so would behave the same as the baseline model, BRL. As we increase the value of λ, the effect of the structure prior would have an increased influence over the likelihood term in Equation 5.
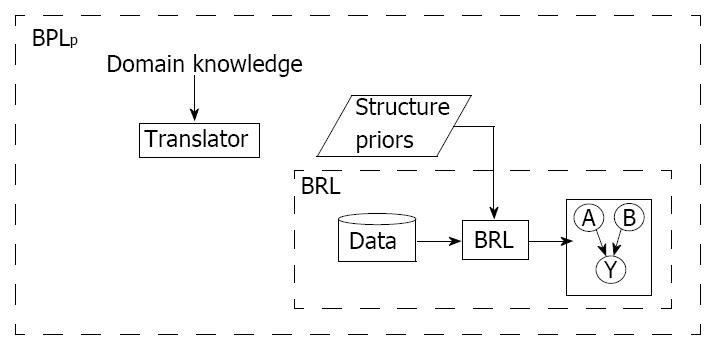
To summarize, BRLp uses a heuristic score called the BDeu score, shown in Equation 5, and encodes the structure prior in that score using Equation 8. The BRLp framework is shown in Figure 1. The inner dotted box, labeled “BRL”, is the classic BRL without prior knowledge, which takes in an input dataset, uses BRL algorithm to learn and output a model. The outer dotted box is our extension, BRLp that can incorporate domain knowledge. The translator process, currently done manually, converts knowledge from various sources to input into Equation 8.
In this section, we describe our experiment design that we used to demonstrate the functionality of BRLp. We examined its behavior on both, simulated dataset, and on a real-world dataset. We were mainly interested in the ability of BRLp to incorporate the supplied prior domain knowledge with respect to the structure prior hyperparameter λ. Additionally, we also monitored the changes in the predictive power of the learned model resulting from the influence of the supplied prior domain knowledge. We studied the functionality of BRLp on a simulated dataset, and then on a real-world dataset. Each is described, in detail, in the following sub-sections.
Simulated data analysis: We first generated simulated data to study the behavior of BRLp. We can control the properties of the simulated dataset, which gave us a controlled environment to check if BRLp was behaving as we expected on a dataset with the specified properties.
Data generation: We generated a simulated dataset with 1000 variables in addition to the target variable, T. We show the data-generating graph in Figure 2. Out of the 1000 candidate variables that can predict T, only one variable, R1000, is relevant. A relevant variable is a variable that helps to predict T. All the remaining 999 variables, {I1...I1000}, are irrelevant. Irrelevant variables are random values that do not help predict T. All the random variables in the graph are binary {0, 1}. The conditional distributions in the graph are Bernoulli with the success parameter p depending upon the value instantiation of their parent variables. The irrelevant and relevant variable values were randomly sampled with p = 0.5. The T variable value was sampled with p = 0.9 if its parent, R1000, took the value 1, and p = 0.1 otherwise.
Data background knowledge: In a simulation problem, we already knew the true data-generating graph as shown in Figure 2. We knew that in the learned network structure from BRLp, there should be an edge present between R1000 and T. So, in Equation 8, the positive edge-set only contained this edge, E+ = {(R1000, T)}. All the edges between irrelevant variables and T should be absent in the BRLp model, so they went to the negative edge-set, E+ = { (Ik, T);k = 1...999}. We evaluated the impact of the λ hyperparameter value of the structure prior on the final model learned by BRLp.
Methods evaluated: We evaluated the method BRLp here. We set the user-defined, search algorithm parameter of BRLp of maximum conjuncts (constraint on maximum number of parents of T) to 8. We evaluated the effect of the hyperparameter λ by assigning =its values λ={0,1,2,3,4,5,6,7,8,9,10}. The value of λ = 0 represents the baseline model of BRL with no structure priors.
Evaluation metrics: We evaluated BRLp with two metrics: (1) graph edit distance (GED); and (2) area under the receiver operator characteristics curve (AUC). We evaluated them over 5 runs of 10-fold cross-validation. In each run, the dataset was randomly shuffled to produce a different set of 10 stratified folds. GED measures how much of the prior domain knowledge gets incorporated into the model learning process. Specifically, how much does the model learned by BRLp agree with the supplied prior knowledge? This metric is described in detail in the next paragraph. We monitored the BRLp model predictive power by measuring the average AUC across the 5 runs of 10-fold cross-validation. The AUC helped us monitor the influence of structure priors in model predictive performance.
GED[14] is a metric of similarity between two graphs. In this experiment, we compared two constrained BNs. Specifically, we were interested in measuring how closely our BRLp predicted BN, ({B}_S)^ (learned by BRLp) resembled the true BN, BS, which generated the simulated dataset (Figure 2 in this experiment). This was used to estimate the value of adding structure prior knowledge for model learning when the true model is available for comparison. We computed this metric using Equation 9.
Here, dV min = [BS, ({B}_S)^] is a function that returns the GED between the two BNs. A specific ei is an edit operation to transform one graph into another. For the constrained BN we have two available edit operations - delete edge, and insert edge. There is a cost c (ei) associated with each edit operation. We set c (ei) = -1, for both the edit operations. A v is an edit path containing a sequence of edit operations to transform graph BS into ({B}_S)^. The set γ[BS, ({B}_S)^] is a set of all possible edit paths. To compute the graph edit distance, we find the edit path, v, that minimizes the overall cost and then return this minimum cost value indicating the minimum number of operations needed to transform one graph to another. Therefore, an edit distance of 0 indicates that the predicted graph is identical to the true graph. Since the maximum parents resulted from BRL is constrained to 8 from the user parameter, the worst possible model contains all 8 irrelevant variables. So, we get dV min = 9 (8 edge deletion operations from irrelevant variables, 1 insert edge operation to the relevant variables).
Real-world lung cancer prognostic biomarker data analysis: We obtained a real-world dataset for our analysis from Gene Expression Omnibus[15] (GEO), a public gene-expression data repository. We extracted the dataset from a study[16] that collected both tumor and normal tissue samples from 60 female non-small cell lung cancer (NSCLC) patients in Taiwan. As a result, there were 120 samples in this dataset (60 patients, each with paired tumor and normal tissue). RNA was extracted from these paired tumor and normal tissues for gene expression analysis on the Affymetrix Human Genome U133 Plus 2.0 Array platform. The platform has 54675 probes. The accession ID for this study on GEO database is GSE19804.
Data pre-processing: The raw dataset extracted from GEO contained 54675 probes and 120 instances. We needed to pre-process the data to prepare it for data analysis. The dataset pre-processing was done using Bioconductor (version 3.6) packages in R (version 3.4.3). We extracted the raw dataset using the affy package[17]. We used Robust Multichip Analysis (RMA) for background correction, quantile normalization, and probe summarization. We mapped probes to the genes they represented. Multiple probes can map to a single gene. In the final dataset, we would like to have just one random variable representing a unique gene. Among the multiple probes that map to a single gene, we chose the probe with the largest inter-quantile range to represent the gene. This process is called inter-quantile range (IQR) filtering. Finally, we also extracted the tissue phenotype (tumor or normal) for each sample and add to this dataset. The outcome variable of interest was this tissue phenotype. After this pre-processing step, we were left with 16382 genes. So, the final dataset for our analysis had 16382 variables and 120 instances. The R script we used for data pre-processing is available in the GitHub repository linked in the Conclusion section.
Many classification algorithms, including BRL, cannot handle continuous-valued variables, and require the input data to be discretized. Moreover, supervised discretization can help improve the performance of several classifiers including Support Vector Machines and Random Forests[18]. This is because supervised discretization acts as a feature selector that only retains variables with meaningful discretization bins. Biomedical datasets are high dimensional, there can be many noisy and redundant variables. Supervised discretization can help remove some of these variables from the model learning process. We discretized the dataset using efficient Bayesian discretization (EBD), a supervised discretization method, which has been shown to obtain better classification performance and stability but less robust when compared to the popular Fayyad-Irani supervised discretization method on several biomedical datasets[19]. We set the user-defined lambda parameter of EBD, to 0.5, as the recommended default value in the paper. During model learning, we split the data into 10 folds for cross-validation. For each train-test fold pair, supervised discretization bins were learned on the train dataset alone. The learned bins were applied to the test dataset. So, during supervised discretization, we did not look at the test dataset.
Data background knowledge: We explored the medical literature for known prognostic markers that may assist in model learning with BRLp. Before exploring, we first sought to understand more about the dataset, which turned out to have some interesting characteristics making it highly worthy of study. Of note, only tissue samples taken from non-smokers who were all women, who had contracted lung cancer were analyzed in this study. Table 1 summarizes some clinical features known about the 60 Taiwanese NSCLC patients studied in the dataset as described in the paper of the study[16].
| Attribute | Value | n (%) |
| Gender | Women | 60 (100) |
| Men | 0 (0) | |
| Tumor type | Adenocarcinoma | 56 (93) |
| Bronchioloalveolar carcinoma | 3 (5) | |
| Squamous | 1 (2) | |
| Others | 0 (0) | |
| Smoking history | Yes | 0 (0) |
| No | 60 (100) |
We noted from the Table 1 that the subjects in the dataset were all women (60 out of 60 patients), contain mainly adenocarcinoma patients (56 out of 60 patients), and none of them had any smoking history (60 out of 60 patients). Additionally, we also knew that all the patients were from Taiwan. So, we explored the medical literature to find known prognostic markers for this sub-population. Epidermal growth factor receptor (EGFR), a receptor tyrosine kinase is prognostic marker known to be frequently over-expressed in NSCLC[20]. EGFR encodes a transmembrane glycoprotein, a receptor for members of the epidermal growth factor family. A ligand binding to this receptor induces dimerization and tyrosine autophosphorylation, and leads to cell proliferation (referred from RefSeq, June 2016). In NSCLC patients, Shigematsu et al[21] observed that EGFR domain mutations are statistically significantly more frequent in women than men (42% vs 14%), in adenocarcinomas than other histologies (40% vs 3%), in non-smokers than smokers (51% vs 10%), and in East Asians than other ethnicities (30% vs 8%); all with a P-value of < 0.001. This description is very similar to the subjects in the dataset we are studying. Therefore, EGFR gene expression was potentially a good candidate to be incorporated as prior domain knowledge into model learning with BRLp on this dataset.
Methods compared: We again evaluated BRLp here. We set its of maximum conjuncts to 8. We evaluated the effect of the hyperparameter λ by assigning it values of λ = {0,1,2,4,6,8,10,20}. The value λ = 0 represents the baseline model of BRL with no structure priors. We included λ = 20, to study the scenario where the structure priors overwhelmingly dominates the likelihood score. Additionally, we compared these models with some state-of-the-art classifiers including three interpretable class of classifiers namely - C4.5[22], RIPPER[23], and PART[24]; and three complex and non-interpretable classifiers namely- Random Forests[25], naïve Bayes[26], and Support Vector Machines[27]. C4.5[22] is a popular decision tree learning algorithm, where each path of the decision tree can be interpreted as rules. RIPPER[23] (Repeated Incremental Pruning to Produce Error Reduction) is a propositional rule learning algorithm that uses a divide-and-conquer strategy during model training. PART[24] is a rule learning method that combines the approaches of both C4.5 and RIPPER by building partial decision trees, inferring rules from the trees, and using a divide-and-conquer strategy to build the rule model. Random Forest[25] is an ensemble learning method that learns a number of decision trees during training, and combines predictions from them during inference. The naive Bayes[26] classifier is a simple probabilistic classifier that learns a network with strong independence assumption between the variables, and uses the Bayes theorem for inference from the learned network. Support Vector Machines[27] is an algorithm that learns a hyperplane function to differentiate the classes in the problem space. We ran these classifiers from the Weka[28] workbench (version 3.8.1) using the default parameters for each classifier.
Evaluation metrics: We evaluated BRLp with two metrics: (1) Prior Frequency (PF); and (2) AUC. We evaluated the dataset over 5 runs of 10-fold cross-validation. For this real-world scenario, we used PF to measure the gain of the background knowledge into BRLp. With the simulated dataset, we had evaluated using GED because we knew the true data-generating graph. In most real-world problems, we do not know the true model that generated the data and so, we cannot use GED. PF measures the fraction of models learned on each of the 50 folds (5 runs of 10-fold cross-validation) that incorporates the specified prior domain knowledge. In this experiment, we measured the fraction of the models that contained an edge between EGFR and T in the learned BRLp model.
In this section, we present the results from our experiments examining the effects of the λ hyperparameter of the structure prior, and consequentially the influence of the specified prior knowledge on model learning. We show our results using the simulated data first, and then from the real-world lung cancer prognostic dataset.
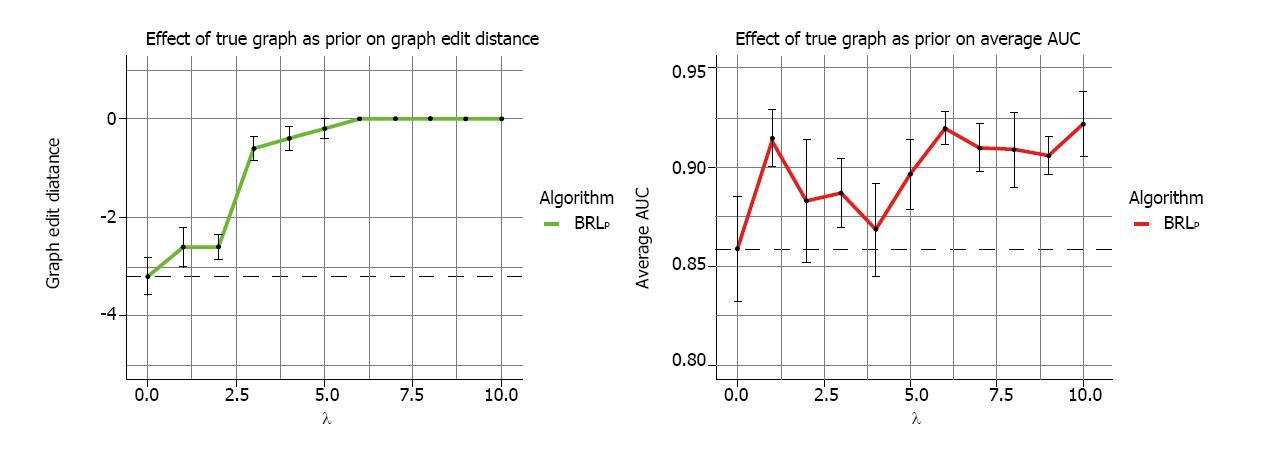
The results from the 5 runs of 10-fold cross-validation are summarized in Figure 3. In Figure 3A, the various values of the hyperparameter λ is shown in the x-axis, while the y-axis shows the average GED. This average is obtained across the 10-folds of each run, and then averaged across the 5 runs. Each data-point in the graph is this average deviation from the true model as measured by the GED, and the error bars represent the standard error of mean. The dotted line shows the value of BRLp with λ = 0, which as we mentioned earlier is the same as BRL, where we use uninformative priors. We saw that even with λ = 1, the structure priors helped improve the GED thereby bringing the learned model closer to the data-generating model. We saw a sharp gain of GED from λ = 2 to 3. For λ ≥ 6, BRLp returned the true data-generating model specified by the structure priors. This showed that BRLp effectively and correctly incorporates the specified domain knowledge. The degree of incorporation is controlled by λ.
Figure 3B displays the average AUC. The overall trend is a gain in AUC but the trend is noisy, especially with low λ values when the GED > 0. This region indicated models that picked up irrelevant variables, which were spurious and were associated with T, by chance. Their AUC fluctuated a lot because random associations were found. When λ ≥ 6, the GED reached the perfect 0, we saw a rise in AUC. The noise reduced in this region of the graph. Random samplings from our simulation generated slightly different values of the parameters, which were reflected in the fluctuations here. So, from the AUC graph we saw a gradual gain in predictive performance with the incorporation of prior knowledge of the truth.
Figure 4 shows a BRLp rule model obtained when λ = 10, which achieved the largest average AUC from our experiments (AUC = 0.92). The particular run achieved an AUC of 0.96 on the 10-fold cross-validation and a GED of a perfect 0. The posterior probability was computed using Equation 6. TP and FP refers to the total true positives and false positives. Pos and Neg are the total positives and negative examples. Our simulation design only had one relevant variable, R1000, and 999 irrelevant variables, {I1...I1000}. The rule model in Figure 4 correctly picked up only the relevant variable. We had designed the simulation such that if the relevant variable took the value 1, then T would be sampled with a Bernouli distribution with p = 0.9, this was reflected in Rule 2. So, BRLp accurately retrieved the true data-generating model assisted by informed structure priors.
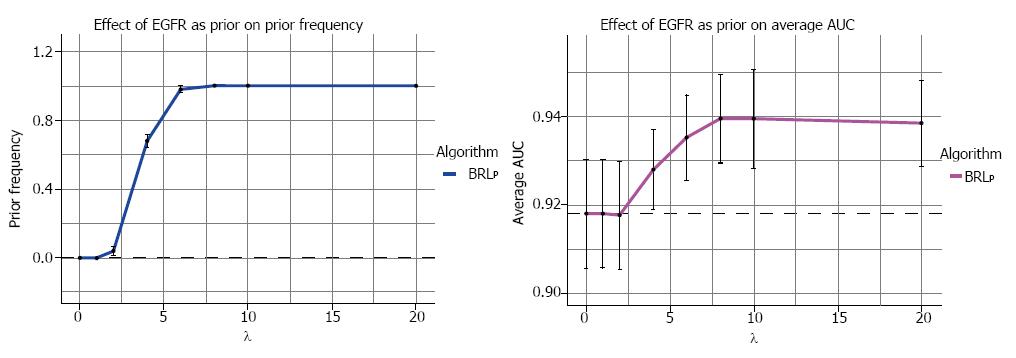
The results from the 5 runs of 10-fold cross-validation on the real-world lung cancer prognostic dataset are summarized in Figure 5. We specified the structure prior of an edge between EGFR and the outcome Class variable to be present. We altered the values of λ and observed its effect on the learned model. Figure 5A, shows the effect of the different values of λ on PF, the fraction of models that contained EGFR. From λ = 2 to 6, we saw a steep gain in PF. For λ ≥ 8, EGFR was present in every learned model. This again showed that BRLp effectively incorporated the specified prior knowledge and the λ hyperparameter allowed the user to determine the degree of incorporation of this knowledge by BRLp.
Figure 5B, shows the gain of average AUC across 5 runs of 10-fold cross-validation. We observe a steady gain of AUC for λ > 2. For λ ≥ 8, the AUC gain tapers off. The results show that the EGFR prior knowledge helped improve the AUC of BRLp.
BRLp with λ = 8 generated the highest average AUC of 0.935. Figure 6 shows the rule model from one of the runs, which had achieved a cross-validation AUC of 0.967 and PF of 1. Rule 1 had the highest amount of evidence (38 true positives and no false positives) for the outcome Control (normal tissue). This rule had the EGFR value range from negative infinity to 10.8. In other words, EGFR was under-expressed in these 38 normal tissue instances. Rule 15 had the highest amount of evidence (15 true positives) for the outcome Case. This rule had EGFR value range from 10.8 to positive infinity. In other words, EGFR was over-expressed in these 15 tumor tissue instances. These rules also lent support to what we had found in the literature about EGFR being over-expressed in tumor cells. In addition to EGFR, which was incorporated from the structure prior, the model picked up 3 other variables during model learning from the dataset. They were ephrin A4 (EFNA4), killer cell lectin like receptor G2 (KLRG2), and C2 calcium dependent domain containing 6 (C2CD6).
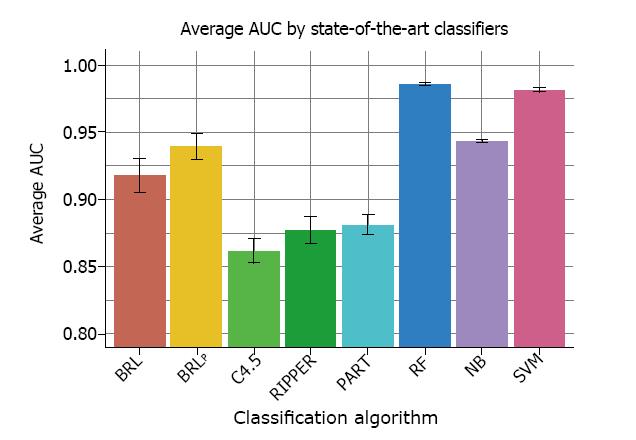
Finally, we compared two BRLp models with state-of-the-art classifiers using average AUC achieved across 5 runs of 10-fold cross-validation. The two BRLp models were (1) with λ = 0, which represented the baseline BRL model with uninformative priors, and (2) with λ = 8 that incorporated EGFR into the structure prior, which achieved the highest average AUC of 0.935. The state-of-the-art classifiers compared were C4.5, RIPPER, PART, Random Forests, naïve Bayes, and Support Vector Machines. This comparison is shown in Figure 7.
The first two bars in Figure 7 are BRLp algorithms, BRLp with λ = 0 is indicated as BRL, and then BRLp with λ = 8. We saw a gain in performance crom incorporating EGFR as structure priors. The next three bars - C4.5, RIPPER, and PART are interpretable class of models, which are human readable. C4.5 is a decision tree learning algorithm. RIPPER and PART are rule learning algorithms. We noticed that these three algorithms performed worse than both BRLp algorithms in this dataset. The last three bars in Figure 7 are - Random Forest, naïve Bayes, and Support Vector Machines. These are examples of complex models that use all variables in the dataset to generate a classifier. It is not easy to explain the reasoning behind their predictions. But all three algorithms here outperformed BRLp on this dataset. This comparison shows the trade-off of predictive performance and interpretability. On this dataset, BRLp offered an interpretable model that outperformed other popular interpretable models but did not perform as well as the complex models.
An important practical consideration to note while specifying structure priors is to avoid specifying priors that introduce bias into the model search. Informative priors can be biased if they are inferred based on the predictions, of some predictive model, on the test dataset. For example, if we notice that our learned model predicts poorly on a subset of test instances, and we notice some independent variable(s) strongly associated with the target variable in that subset of test instances. Specifying, our newly found association from the predictions on the test dataset, into the structure priors to re-learn the model will return a biased model and must be avoided.
Mukherjee and Speed[8] show how the general form of the score in Equation 7 can be extended to incorporate other kinds of prior knowledge including rewarding network sparsity, where structure priors can be used as a regularization term. In the introduction section, we had discussed other sources of prior knowledge than literature, including - input from a domain expert (e.g., A physician), domain ontology (e.g., Gene Ontology), and models learned from other related datasets. In the future, we will explore the incorporation of knowledge from these other sources. In novel biomarker discovery, we could place all of our known knowledge into the negative edge-set in Equation 8. Models learned from such a structure prior would be penalized for learning already known biomarkers and would encourage discovery of novel biomarkers. We used an instantiation of the general form of the score, in Equation 7, where the relative weights, wi, of each of ith network are set to 1. It would be interesting to explore different relative weights for different network features and see its impact on model learning. In this paper, we performed a grid search over the hyperparameter λ. We would like to explore if we can come up with better ways to optimize the value of this hyperparameter.
In this paper, we implemented BRLp, a method that extended BRL to allow it to integrate prior domain knowledge using structure priors into the model learning process. We demonstrated the ability of BRLp to incorporate this knowledge on simulated data and a real-world lung cancer prognostic dataset. We observed that the λ hyperparameter allowed us to control the degree of incorporation of prior knowledge. This parameter can be helpful if we were uncertain about our specified prior knowledge. We also observed that relevant prior knowledge could sometimes help improve the predictive performance of BRLp. Methods developed in this paper, the simulation data experiment code, and the R script for data extraction and processing of the prognostic dataset, are all made publicly available in an online repository (https://github.com/jeya-pitt/brl-structure-priors). We envision that BRLp will be very beneficial in data mining tasks across domains where some prior domain knowledge is available.
Biomedicine is increasingly a data-driven science, owing largely to the explosion in data, especially from the development of high-throughput technologies. Such datasets often suffer from the problem of high-dimensionality, where a very large number of candidate variables can explain the outcome variable of interest but have few instances to support any model hypothesis. In many applications, in addition to the data itself, some domain knowledge is available that may assist in the data mining process to help learn more meaningful models. It is important to develop data mining tools to leverage this available domain knowledge. However, currently, there is a dearth of data mining methods that can incorporate this available domain knowledge.
Developing data mining methods that can incorporate domain knowledge will help learn more meaningful models and will benefit many domains, especially the ones that suffer from data scarcity but have some domain knowledge that can assist with the data mining process (for example - biomedicine).
In this work, our objective was to extend a rule learning algorithm, called Bayesian rule learning (BRL), to make it capable of incorporating prior domain knowledge. BRL is a good candidate because it has been shown to be successful in application to high-dimensional biomedical data analysis tasks. We implemented such a tool, called BRLp that has tunable priors, which means the user can control the degree of incorporation of their specified knowledge. BRLp is a novel data mining tool that allows the user to specify their domain knowledge (including uncertain domain knowledge) and incorporates it into the model search process.
BRL searches over a space of Bayesian belief network models (BNs) to find the optimal network and infers a rule set from that model. We implemented a way for the BN to incorporate informative priors, a distribution encoding the relative importance of each model prior to seeing the training data. This allowed BRL to incorporate user-specified domain knowledge into the data mining process called BRLp. BRLp has a hyperparameter λ that allows the user to adjust the degree of incorporation of their specified prior knowledge.
We evaluated BRLp by comparing it to BRL (without informative priors) and other state-of-the-art classifiers on a simple simulated dataset, and a real-world lung cancer prognostic dataset. We measured the degree of acceptance of the specified prior knowledge with respect to the hyperparameter λ in BRLp. We also observed the changes in predictive power using AUC.
We observed, in both the experiments with simulated data and the real-world lung cancer prognostic data that with increasing values of λ the degree of incorporation of the specified prior knowledge also increased. We also observed that specifying prior knowledge relevant to the problem dataset could sometimes help find models with better predictive performance. When BRLp is compared to the state-of-the-art classifiers, we observed that it performed better than other interpretable models but the more complex and non-interpretable models achieved better predictive performance than BRLp.
BRLp allows the user to incorporate their specified domain knowledge into the data mining task and allows them to control the degree of incorporation with a hyperparameter. This is a novel rule learning algorithm that we have made available to the general public via GitHub. We anticipate its use in many applications especially the ones suffering from data scarcity but have additional domain knowledge available that may assist in the data mining task.
In this paper, we explored specifications of simple domain knowledge. We need to further explore the incorporation of more complex forms of knowledge. In this paper, we incorporate domain knowledge from literature. We also want to explore domain knowledge available in other sources. These future directions may motivate further developments to BRLp.
Specialty type: Oncology
Country of origin: United States
Peer-review report classification
Grade A (Excellent): 0
Grade B (Very good): B, B, B
Grade C (Good): 0
Grade D (Fair): 0
Grade E (Poor): 0
P- Reviewer: Gadbail AR, To KKW, Yao DF S- Editor: Ma YJ L- Editor: A E- Editor: Wu YXJ
| 1. | Fayyad UM, Piatetsky-Shapiro G, Smyth P, Uthurusamy R. Advances in knowledge discovery and data mining. Technometrics. 1996;40: xviii. |
| 2. | Esfandiari N, Babavalian MR, Moghadam AME, Tabar VK. Knowledge discovery in medicine: Current issue and future trend. Expert Syst Appl. 2014;41:4434-4463. [DOI] [Full Text] |
| 3. | Fayyad U, PiatetskyShapiro G, Smyth P. From data mining to knowledge discovery in databases. Ai Magazine. 1996;17:37-54. |
| 4. | Gopalakrishnan V, Lustgarten JL, Visweswaran S, Cooper GF. Bayesian Rule Learning for Biomedical Data Mining. Bioinformatics. 2010;26:668-675. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 30] [Cited by in RCA: 25] [Article Influence: 1.7] [Reference Citation Analysis (0)] |
| 5. | Lustgarten JL, Balasubramanian JB, Visweswaran S, Gopalakrishnan V. Learning Parsimonious Classification Rules from Gene Expression Data Using Bayesian Networks with Local Structure. Data. 2017;2:5. [RCA] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 5] [Cited by in RCA: 7] [Article Influence: 0.9] [Reference Citation Analysis (0)] |
| 6. | Buntine W. Theory refinement on Bayesian networks. Uncertainty Proceedings. 1991;14:52-60. [DOI] [Full Text] |
| 7. | Castelo R, Siebes A. Priors on network structures. Biasing the search for Bayesian networks. Int J Approx Reason. 2000;24:39-57. [RCA] [DOI] [Full Text] [Cited by in Crossref: 25] [Cited by in RCA: 25] [Article Influence: 1.0] [Reference Citation Analysis (0)] |
| 8. | Mukherjee S, Speed TP. Network inference using informative priors. Proc Natl Acad Sci USA. 2008;105:14313-14318. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 127] [Cited by in RCA: 113] [Article Influence: 6.6] [Reference Citation Analysis (0)] |
| 9. | Koller D, Friedman N. Probabilistic Graphical Models: Principles and Techniques - Adaptive Computation and Machine Learning. MIT Press. 2009;161-168. |
| 10. | Chickering DM, Heckerman D, Meek C. A Bayesian approach to learning Bayesian networks with local structure. Thirteenth Conference on Uncertainty in Artificia. 1997;80-89. |
| 11. | Balasubramanian JB, Visweswaran S, Cooper GF, Gopalakrishnan V. Selective model averaging with bayesian rule learning for predictive biomedicine. AMIA Jt Summits Transl Sci Proc. 2014;2014:17-22. [PubMed] |
| 12. | Harary F, Palmer EM. Graphical enumeration. Elsevier. 2014;. |
| 13. | Jeffreys H. The theory of probability. OUP Oxford. 1998;. |
| 14. | Riesen K. Structural pattern recognition with graph edit distance. Springer Publishing Company, Incorporated. 2016;. |
| 15. | Barrett T, Wilhite SE, Ledoux P, Evangelista C, Kim IF, Tomashevsky M, Marshall KA, Phillippy KH, Sherman PM, Holko M. NCBI GEO: archive for functional genomics data sets--update. Nucleic Acids Res. 2013;41:D991-D995. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 4527] [Cited by in RCA: 6765] [Article Influence: 520.4] [Reference Citation Analysis (0)] |
| 16. | Lu TP, Tsai MH, Lee JM, Hsu CP, Chen PC, Lin CW, Shih JY, Yang PC, Hsiao CK, Lai LC. Identification of a novel biomarker, SEMA5A, for non-small cell lung carcinoma in nonsmoking women. Cancer Epidemiol Biomarkers Prev. 2010;19:2590-2597. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 197] [Cited by in RCA: 225] [Article Influence: 15.0] [Reference Citation Analysis (0)] |
| 17. | Gautier L, Cope L, Bolstad BM, Irizarry RA. affy--analysis of Affymetrix GeneChip data at the probe level. Bioinformatics. 2004;20:307-315. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 3737] [Cited by in RCA: 4047] [Article Influence: 192.7] [Reference Citation Analysis (0)] |
| 18. | Lustgarten JL, Gopalakrishnan V, Grover H, Visweswaran S. Improving classification performance with discretization on biomedical datasets. AMIA Annu Symp Proc. 2008;445-449. [PubMed] |
| 19. | Lustgarten JL, Visweswaran S, Gopalakrishnan V, Cooper GF. Application of an efficient Bayesian discretization method to biomedical data. BMC Bioinformatics. 2011;12:309. [RCA] [PubMed] [DOI] [Full Text] [Full Text (PDF)] [Cited by in Crossref: 28] [Cited by in RCA: 29] [Article Influence: 2.1] [Reference Citation Analysis (0)] |
| 20. | Bethune G, Bethune D, Ridgway N, Xu Z. Epidermal growth factor receptor (EGFR) in lung cancer: an overview and update. J Thorac Dis. 2010;2:48-51. [PubMed] |
| 21. | Shigematsu H, Lin L, Takahashi T, Nomura M, Suzuki M, Wistuba II, Fong KM, Lee H, Toyooka S, Shimizu N. Clinical and biological features associated with epidermal growth factor receptor gene mutations in lung cancers. J Natl Cancer Inst. 2005;97:339-346. [RCA] [PubMed] [DOI] [Full Text] [Cited by in Crossref: 1745] [Cited by in RCA: 1901] [Article Influence: 95.1] [Reference Citation Analysis (0)] |
| 23. | Cohen WW. Fast effective rule induction. Machine Learning Proceedings 1995. Proceedings of the Twelfth International Conference on Machine Learning, Tahoe City, California, July 9–12. 1995;115-123. [DOI] [Full Text] |
| 24. | Frank E, Witten IH. Generating accurate rule sets without global optimization. Machine Learning. Fifteenth International Conference. 1998;144-151. [PubMed] |
| 25. | Breiman L. Random forests. Machine Learning. 2001;45:5-32. [RCA] [DOI] [Full Text] [Cited by in Crossref: 56052] [Cited by in RCA: 34065] [Article Influence: 2838.8] [Reference Citation Analysis (0)] |
| 26. | John GH, Langley P, editors . Estimating continuous distributions in Bayesian classifiers. Proceedings of the Eleventh conference on Uncertainty in artificial intelligence, 1995; Morgan Kaufmann Publishers Inc. 2013;338-345. |
| 27. | Platt JC. Fast training of support vector machines using sequential minimal optimization. MIT Press Cambridge, MA, USA. 1999;185-208. [PubMed] |
| 28. | Frank E, Hall M, Witten IH. The WEKA Workbench. Online Appendix for “Data Mining: Practical Machine Learning Tools and Techniques”: Morgan Kaufmann 2016; . |