Cancer prognosis using support vector regression in imaging modality

Abstract

The proposed techniques investigate the strength of support vector regression (SVR) in cancer prognosis using imaging features. Cancer image features were extracted from patients and recorded into censored data. To employ censored data for prognosis, SVR methods are needed to be adapted to uncertain targets. The effectiveness of two principle breast features, tumor size and lymph node status, was demonstrated by the combination of sampling and feature selection methods. In sampling, breast data were stratified according to tumor size and lymph node status. Three types of feature selection methods comprised of no selection, individual feature selection, and feature subset forward selection, were employed. The prognosis results were evaluated by comparative study using the following performance metrics: concordance index (CI) and Brier score (BS). Cox regression was employed to compare the results. The support vector regression method (SVCR) performs similarly to Cox regression in three feature selection methods and better than Cox regression in non-feature selection methods measured by CI and BS. Feature selection methods can improve the performance of Cox regression measured by CI. Among all cross validation results, stratified sampling of tumor size achieves the best regression results for both feature selection and non-feature selection methods. The SVCR regression results, perform better than Cox regression when the techniques are used with either CI or BS. The best CI value in the validation results is 0.6845. The best CI value corresponds to the best BS value 0.2065, which were obtained in the combination of SVCR, individual feature selection, and stratified sampling of the number of positive lymph nodes. In addition, we also observe that SVCR performs more consistently than Cox regression in all prognosis studies. The feature selection method does not have a significant impact on the metric values, especially on CI. We conclude that the combinational methods of SVCR, feature selection, and sampling can improve cancer prognosis, but more significant features may further enhance cancer prognosis accuracy.

Key Words: Breast cancer imaging; Cancer prognosis; Sampling; Support vector regression

INTRODUCTION

Cancer causes millions of deaths every year worldwide, and the number of these deaths is constantly on the rise[1]. The World Health Organization (WHO) estimates that in 2030, 12 million people worldwide will die from cancer or cancer-related complications. This number represents a possible 4.6 million increase from the recorded 7.4 million cancer-related deaths that occurred in 2004. Extensive research into cancer and cancer-related problems helps average people understand behavioral and environmental causes of cancer. The discovery and understanding of cancer pathology, in turn, can help people prevent, detect, and control and treat cancer. This discovery is important, as it has been shown that one-third of cancer cases can be controlled in cases where early detection, diagnosis, prognosis, and treatment occur.

Cancer prognosis is the long-term prediction of cancer susceptibility, recurrence, and survivability[2]. Early prognosis of cancer can improve the survival rate for cancer patients. Using imaging modalities, such as functional magnetic resonance imaging (fMRI), positron emission tomography (PET), and computed tomography (CT), histological information about patients can be integrated for cancer diagnosis and prognosis[3]. High throughput imaging technologies lead to a large number of features and parameters in molecular, cellular, and organic images, which can support the clinical prognosis of cancer. However, large amounts of imagery data overwhelm clinicians involved in oncological decision making. The need to analyze and understand these large amounts of data have led to the development of computational statistical machine learning and data mining methods for oncological imagery.

Breast cancer is the most frequent type of cancer, and is the leading cause of death among women (ranking first in the world and second in the USA as a cause of cancer-related deaths among women)[1,4]. Breast imaging techniques, including ultrasound, mammography, MRI, and PET, provide mechanisms to screen and diagnose breast tumors based on the geometry level (e.g. tumor and/or tissue shape) and the cell level (e.g. tumor cells)[5]. The use of in vivo molecular and cellular imaging of breast cancer has increased because it is advantageous for bridging breast and cellular macrofeatures. The screening and measurement of breast cancer at the molecular and cellular levels also derives from our knowledge that cancer begins in a single cell, transforming that cell from a normal state to a tumor and cloning the tumor to multiple cells, also called metastasizing. Thus, a cancer prognosis based on the processing and analysis of cell imaging is highly efficient and effective[3,6].

Imaging techniques that are entirely non-invasive cannot provide a perfect diagnosis and/or prognosis for a breast cancer case. A traditional biopsy can help clinicians examine the pathology of a breast mass perfectly, but this process causes pain for patients. For example, clinically, tumor size, lymph node status, and metastasis (TNM) are mostly employed in breast staging systems as predicative factors[7,8]. To acquire the TNM information from patients, clinicians need to measure the excised tumor and examine the presence and status of lymph nodes obtained from patients’ axilla. The above invasive operations cause pain in patients’ arms and can further cause infections. Hence, researchers use fine needle aspirations (FNAs) to minimize the invasiveness and enhance the imaging techniques (e.g. mammography) in breast cancer examination and prognosis. To obtain FNAs, clinicians insert a gauge needle into a breast lump and remove a small number of cell samples. Using microscopes, we can capture cell images and examine the features of cells for cancer prognosis. Thus, the prognosis procedure includes three steps: acquisition of cell images using FNAs and imaging techniques, image processing and feature extraction from cellular images, and pattern recognition and prediction using machine learning techniques. The first two steps result in a set of features for breast cancer diagnosis and prognosis. In breast cancer diagnosis, pattern recognition methods provide labels for breast features: benign or malignant. In cases where breast images are labeled malignant, machine-learning methods will be applied to predict the long-term effects of the cancer. Cancer prognosis is difficult because the censored medical data are uncertain information. Censored data are the observations recorded without the precisely known event time during follow-ups in cancer patients, e.g. the survival time of a cancer patient after the tumor was removed by surgery. Censored data include left-censored data and right-censored data. Left censored data are observations of cancer after cancer recurs. This data only include the upper bound of the cancer recurring time (the time at which the clinicians observed the recurrence). Right-censored data are observations of cancer before cancer recurs, e.g. patient dies disease-free. This data only includes the lower bound of cancer recurring time (the time at which the patient dies). Both types of censored data are incomplete and lack specificity required for clinical research. As conventional regression methods were designed to predict certain target values, new algorithms are needed to predict the censored data.

In this paper, we present a novel computational framework for cancer prognosis that uses support vector regression (SVR) and sampling algorithms. We use the publicly available dataset: Wisconsin prognostic breast cancer (WPBC)[9] to evaluate the strength of SVR for cancer prognosis. In the next section, we briefly describe the WPBC dataset. Then, we describe how the SVR method is applied for cancer prognosis. Next, we demonstrate the experimental prognosis results using various sampling methods. Finally, we conclude the strength and limitations of using the SVR method in cancer prognosis.

BREAST IMAGING AND CELL FEATURES

The WPBC dataset was collected from several breast cancer cases, and image features were extracted by the researchers in the University of Wisconsin[6]. The dataset largely comprises of 155 patients monitored for recurrence within 24 mo. The data comprises of 30 cytological features and 2 histological features: number of metastasized lymph nodes and tumor size. The records only included the patients who had invasive breast cancer. The images of FNA samples were acquired from the breast masses of the patients. For each image, 30 cell features were extracted to describe the cell nuclei in the image. The imaging cell features include radius, texture, perimeter, area, smoothness, compactness, concavity, concave points, symmetry, and fractal dimension (see the details in[6]). Three descriptors of each feature were recorded for each image in the WPBC dataset: mean, standard deviation, and largest value of the feature. As tumor size, lymph node status, and metastasis (TNM) are clinically employed in breast staging systems as predicative factors[8], tumor size and lymph node status were also collected in measurements of centimeters and number of positive axillary lymph nodes, respectively. There are 198 instances: 151 censored (nonrecurring) instances and 47 recurring instances. For the recurring cases, the recurrence time (left-censored data) was recorded, and for the censored instances, the disease-free time (right-censored data) was recorded. The censored data make the prognosis challenging because of its uncertainty.

In the next section, we review support vector machines (SVM) and SVR methods, and explain the above challenge in depth.

SVM AND SVR

SVM is a machine-learning method that uses support vectors, instead of modeling structures, (e.g. multilayer preceptor), to map inputs to outputs. SVM was introduced by Vapnik[10] as a classification and prediction method. SVM can be applied for both regression and classification. Given a dataset (x_i,y_i), where x_i represents data points using vectors and y_i denotes label of the vector x_i(e.g. y_iε{-1, +1}), SVM algorithms can be applied to classify the data points with the hyperplane that has the maximum distance to the nearest data points on each side.

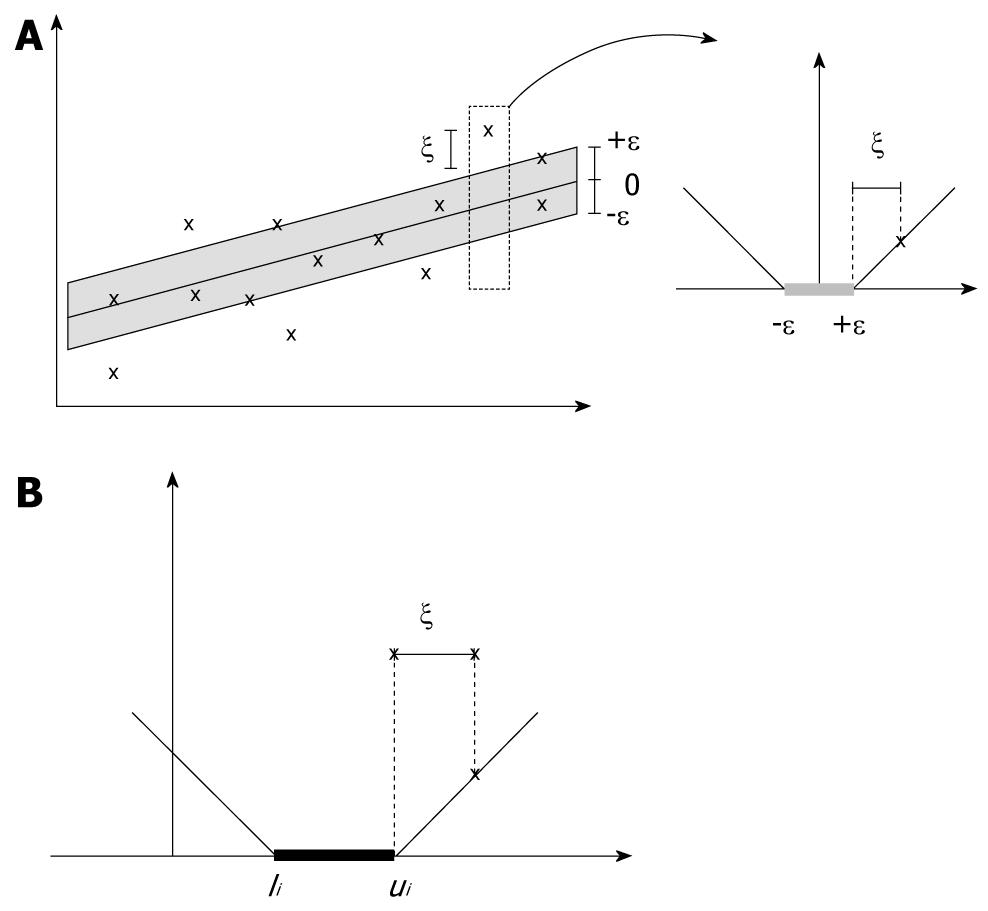
SVR incorporates the concepts of ε-threshold area and loss function into support vector machines to approximate the state value of a given system using feature vectors. In SVR[11], y_i denotes the obtained target value of vector x_i, and f(x_i) denotes the predicted target value of vector x_i. The central motivation for using SVR is to seek the small or flat ε-neighborhood that describes most data points and to panelize the data points that fall outside of ε-neighborhood. As shown in Figure 1A, the data points that fall into ε-insensitive area will have zero-loss and the data points outside of ε neighborhood will have a loss defined by slack variables ξ or ξ*. The slack variables can be defined as a loss function. For example, the ε-insensitive linear loss function is most employed as follows (as shown in Figure 1A): \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} \[ \left| \zeta \right| = \left\{ \begin{array}{l} 0{\rm{ }}when{\rm{ }}\left| \zeta \right| \le \varepsilon \\ \left| \zeta \right| \le \varepsilon {\rm{ }}otherwise{\rm{ }} \\ \end{array} \right. \] \end{document}

Figure 1 ε-insensitive linear loss function (A) and the linear loss function in support vector regression method (B).

Thus, a linear SVR can be formulated formally in the following:

(1) \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} \[ \begin{gathered} \min {\text{ }}\frac{1} {2}\left\| w \right\|^2 + C\sum\limits_{i = 1}^l {\left( {\zeta _i + \zeta _i^* } \right)} \hfill \\ s.t.{\text{ }}\left\{ \begin{gathered} y_i - w^T x_i - b \leqslant \varepsilon + \zeta _i \hfill \\ w^T x_i + b - y_i \leqslant \varepsilon + \zeta _i^* \hfill \\ \zeta _i ,\zeta _i^* \geqslant 0 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \] \end{document}

Where, C is a positive constant that determines the trade-off between the flatness of function and the amount up to which deviations larger than the threshold ε are tolerated.

Using Lagrangian multipliers a_i≥ 0 and a_i^*≥ 0 for the constraints in Equation, and taking derivatives with respect to primal variables, the optimal solution to the above regression formulation is:

(2) \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} \[ f\left( x \right) = \sum\limits_{i = 1}^l {\left( {\alpha _i - \alpha _i^* } \right)\left\langle {x,x_i } \right\rangle + b} \] \end{document}

(3) \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} \[ w = \sum\limits_{i = 1}^l {\left( {\alpha _i - \alpha _i^* } \right)x_i } \] \end{document}

The traditional SVR method has been employed successfully for event prediction because of its robustness and accuracy. However, we can only find few applications using SVR for medical and cancer prognosis, because traditional SVR methods require that the training data have certain target values, while clinicians can only provide uncertain censored target values, e.g. interval target values. Shivaswamy et al[12] proposed a SVR method, called SVCR, to approximate the target values for censored data[12]. We apply the SVCR method in the project. We summarize the SVCR algorithm in the next section.

SVR FOR CENSORED DATA

The SVCR algorithm solves the censored data problem by adapting the loss function to interval values in censored data. Given the interval bounds: lower bound l_i, _i = 1,…n, and upper bound u_i for each censored data (x_i,l_i,u_i), the loss function is defined as:

(4) \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} $c\left( {f\left( {x_i } \right),l_i ,u_i } \right) = \max \left( {l_i - f\left( {x_i } \right),f\left( {x_i } \right) - u_i } \right)$ \end{document}

As illustrated in Figure 1B, the modified loss function in SVCR follows the theory that when the predicted value f(x_i) falls into the interval (l_i,u_i), no penalization is applied in the loss function. Then, the SVR for censored data is formulated as follows:

(5) \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} \[ \begin{gathered} \min {\text{ }}\frac{1} {2}\left\| w \right\|^2 + C\left( {\sum\limits_{i \in U} {\zeta _i } + \sum\limits_{i \in L} {\zeta _i^* } } \right) \hfill \\ s.t.{\text{ }}\left\{ \begin{gathered} w^T x_i + b \geqslant l_i + \zeta _i ,\forall i \in L; \hfill \\ w^T x_i + b \leqslant u_i + \zeta _i^* ,\forall i \in U; \hfill \\ \zeta _i ,\zeta _i^* \geqslant 0. \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \] \end{document}

In the above, U includes the indices of the data points that have a finite right upper bound, and L includes the indices of the data points that have finite left lower bound. Using Lagrangian multipliers and optimization methods, the above problem can be solved by Equation.

COMPARATIVE EVALUATION

To evaluate the strength of SVRC in cancer prognosis using imaging features, we compare the regression results by combining feature selection and sampling methods. We also compare the results of SVRC with those of the conventional prognosis method: Cox regression, using the concordance index (CI) and Brier score (BS) as performance metrics. We review these methods below.

Cox regression[13] is an approach used to measure the effect of a set of features on the event outcomes, e.g. the recurrence of cancer. The Cox regression model uses a hazard function to measure the decline of survival time. Using the hazard function, we can estimate the non-survival (or event) probability at a time point. Given a set of feature values {f_i}, i = 1,…,d, and their associated decline parameters s_i for an individual, the hazard function for that individual is formulated as follows:

(6) \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} $h\left( t \right) = h_0 \left( t \right)\exp \left( {\sum\limits_i {\left( {s_i f_i } \right)} } \right)$ \end{document}

In the above, decline parameters s_i can be approximated using maximum likelihood estimation. We use the above function in Cox regression.

To accurately measure the performance of regression models, we need to investigate the combination of feature subsets which can generate the optimal regression result. Feature selection can be programmed in two directions: by removing the most insignificant individual features one-by-one from the feature set after ranking features according to their significance of prediction results, or by adding the most significant features one-by-one into a feature subset pool after evaluating prediction accuracy of various feature subsets. The ranking of individual features or feature subsets both require metrics, e.g. redundancy and independency. We used the algorithms and metrics proposed in[14] for the above removing or adding feature procedures: individual features are scored by P-value according to their pair-wise association with the events (see details in[14]).

Feature selection methods cannot guarantee a fair validation of regression models because samples may present stratified effects on the model. For example, in clinical research, breast cancer can be graded by tumor size[15]. This stratification indicates that the normal cross-validation method may not be able to generalize the breast cancer prognosis model. One solution to this problem is to randomly select the same number of instances in each grading level of the known grading features for each training dataset. This solution, in turn, evaluates the strength of a regression model at different levels of grading features.

The combination of the above feature selection, sampling, and regression methods results in a set of prognostic values for performance evaluation. Given certain target values, we can calculate prediction errors to measure the accuracy of regression algorithms. However, for cancer data, prediction errors cannot be accessed because most of the data are censored. Predication accuracy can be evaluated by measuring whether the predicted time is ahead of the target value. Researchers have proposed a variety of evaluation metrics to measure the prediction accuracy of methods that use censored data, e.g. CI[16] and BS[17].

The CI is a generalization of the area under the ROC curve. The CI measures the concordance between predicted and observed events. When the predicted probability of events p_t is bigger than the actual occurrence of the events q_t at time t, we say that the prediction result is concordant with the actual event. Hence, the paired comparison between all samples in the given dataset results in the percentage of correct predicted concordances among all sample pairs. In particular, CI = 1, CI = 0.5 and CI = 0 denote the perfect prediction, random prediction, and all-fail prediction, respectively.

BS is a metric function that measures the difference between the predicted probability of events p_t and the occurrence of events q_t at time t. Using the notions above, the BS is formulated as follows for T predicted results:

(7) \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \setlength{\oddsidemargin}{-69pt} \begin{document} $BS = \frac{1} {T}\sum\limits_{t = 1}^T {\left( {p_t - q_t } \right)^2 } $ \end{document}

EXPERIMENTAL RESULTS

In the experiment, we aim to evaluate the power of the SVCR method for cancer prognosis using CI and BS. We evaluate cancer prognosis using the following sampling methods: cross validation of all data, stratified sampling of data for tumor size, and lymph node status. We choose 4-fold cross validation for all experiments and sort the data by their increasing tumor size (noted in centimeters), divide them in bins, and then select the same number of random samples from each bin. It is generally accepted that bigger tumors indicate more cancer complexity. We divide the data into three groups according to tumor size: ≤ 2 cm; 2 cm < but ≤ 5 cm; 5 cm <.

As inflammation and number of lymph nodes are related to breast cancer complexity[15,18], we perform stratified sampling, as above, for the lymph node status as well. We divide the data into three groups according to the number of positive lymph nodes observed in surgery: ≤ 2 cm; 2 cm < but ≤ 5 cm; 5 cm <.

As shown in Tables 1, 2, 3 and 4 we demonstrate the performance of various combinational methods. The results shown in Table 1 are obtained after we delete the four instances that have unknown feature values and use all 32 imaging features for feature selection. We find that SVCR performs consistently in three feature selection methods and performs better than Cox regression in the non-feature selection method by measuring the CI values. This result follows those of Khan et al[19], who obtained test results for the same dataset using Cox and their proposed SVRC algorithm respectively: 0.6031 and 0.6963. They did not describe the feature selection or sampling algorithms in the report[19]. The results shown in Table 1 demonstrate that feature selection methods can improve the performance of Cox regression measured by CI and BS. As shown in Tables 1-4, seven of eight Cox regression results using feature selection perform better than the reported Cox regression result[19]. These results demonstrate that stratified sampling of the number of positive lymph nodes can achieve the best regression results using feature selection methods. This phenomenon corresponds to the conclusion that lymph node status can improve the accuracy of breast cancer prognosis using imaging features, especially when used in correlation with the SVCR method. As shown in Tables 2-4, SVCR regression performs better than Cox regression measured by CI and BS. The best CI value in all validation results is 0.6845, which is almost the same as the 0.6963 using the patented method, SVRC, which was reported in[19]. The above best CI value corresponds to the best BS value 0.2065. In addition, we also observe that SVCR performs more robustly than Cox regression in all prognosis studies. The metric values, especially CI, remain consistent regardless of the feature selection method used in the three sampling data sets.

Table 1 Cross validation results for three feature selection methods using 32 features and 194 instances.

	SVCR			Cox regression
	IS	FFS	NS	IS	FFS	NS
CI	0.6316	0.6333	0.6321	0.6623	0.6333	0.5677
BS	0.2770	0.3609	0.2675	0.2487	0.3319	0.2294

IS: Individual feature selection; FFS: Forward feature selection; NS: Non-feature selection; SVCR: Support vector regression method.

Table 2 Cross validation results for three feature selection methods and without lymph nodes status (32 features) and 198 instances.

	SVCR			Cox regression
	IS	FFS	NS	IS	FFS	NS
CI	0.6532	0.6733	0.6579	0.6465	0.6733	0.5981
BS	0.1969	0.3468	0.2109	0.2504	0.4975	0.3321

IS: Individual feature selection; FFS: Forward feature selection; NS: Non-feature selection; SVCR: Support vector regression method.

Table 3 Cross validation results for three feature selection methods and stratified sampling with respect to tumor size and 194 instances.

	SVCR			Cox regression
	IS	FFS	NS	IS	FFS	NS
CI	0.6390	0.6021	0.6246	0.6244	0.6021	0.5867
BS	0.2904	0.3149	0.3377	0.2588	0.4424	0.3390

IS: Individual feature selection; FFS: Forward feature selection; NS: Non-feature selection; SVCR: Support vector regression method.

Table 4 Cross validation results for three feature selection methods and stratified sampling with respect to lymph nodes status and 194 instances.

	SVCR			Cox regression
	IS	FFS	NS	IS	FFS	NS
CI	0.6845	0.6769	0.6572	0.6341	0.6769	0.6145
BS	0.2065	0.3311	0.2643	0.2147	0.3400	0.3273

IS: Individual feature selection; FFS: Forward feature selection; NS: Non-feature selection; SVCR: Support vector regression method.

CONCLUSION

We conclude that the combinational methods of SVCR, feature selection, and sampling can improve cancer prognosis for the following reasons: First, SVCR performs better than Cox regression for cancer prognosis, measured by CI and BS, particularly when accompanied by feature selection and stratified sampling. Second, feature selection and stratified sampling can improve the accuracy of the SVCR regression results by introducing expert knowledge, such as tumor size and lymph node status. Third, SVCR performs more robustly when used in conjunction with feature selection for cancer prognosis than sampling algorithms do. This conclusion indicates that SVCR inherits the robustness of SVR algorithms. Fourth, we discover that using the current regression model and cancer cell image features, even accompanied by the FNA features and expert knowledge, the prognosis accuracy is lower than the accuracy of traditional biopsies. The discovery of more significant cancer cell image features may improve prognosis accuracy. Lastly, more accurate regression methods are needed for considering the censored data in cancer prognosis.