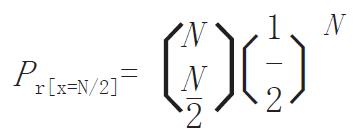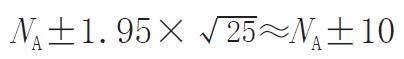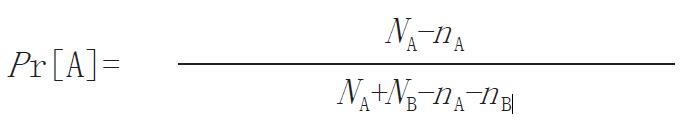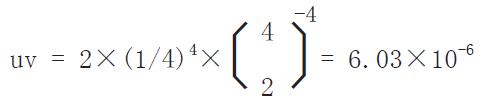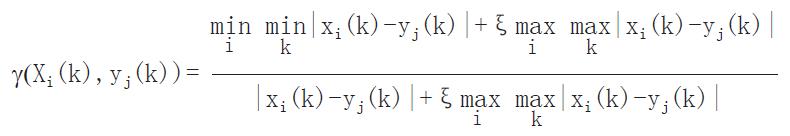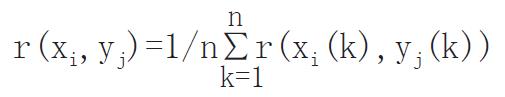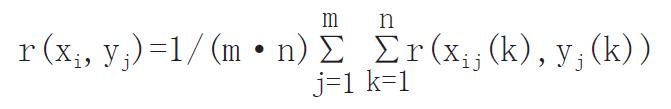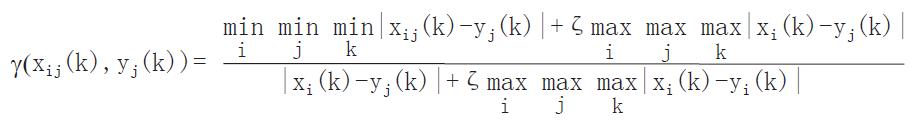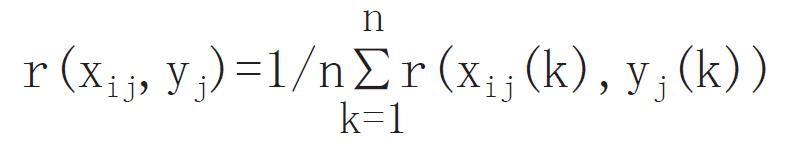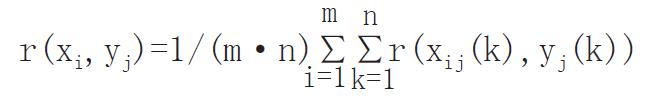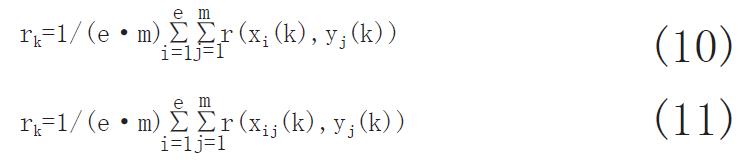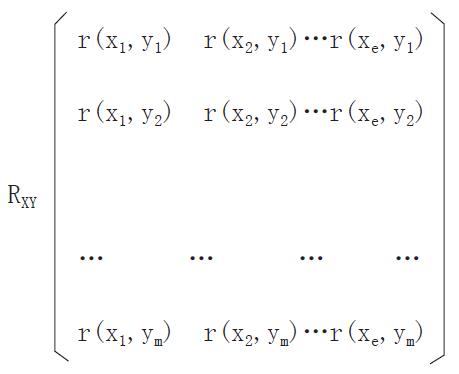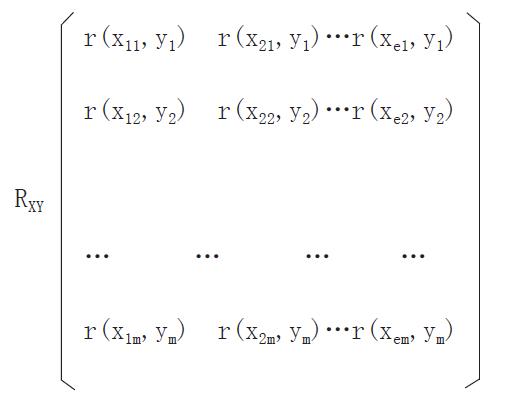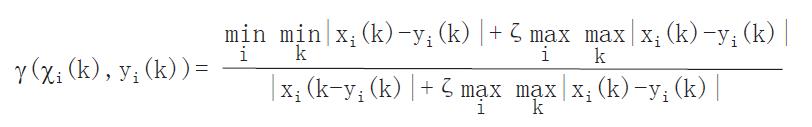修回日期: 2004-12-26
接受日期: 2004-12-31
在线出版日期: 2005-09-28
本文诠释了一些易混淆的统计学概念: 效应与响应, 平衡与均衡, 区组与分层, 研究总体与目标总体. 讨论了不确定原则和治疗意向原则这两个临床试验的重要原则. 对简单随机的局限性提出了改进意见. 还提出了临床试验灰关联方法的两个模型: 评估模型和对比模型.
引文著录: 谭学瑞, 张学中. 临床试验刍议. 世界华人消化杂志 2005; 13(18): 2173-2178
Revised: December 26, 2004
Accepted: December 31, 2004
Published online: September 28, 2005
N/A
- Citation: N/A. N/A. Shijie Huaren Xiaohua Zazhi 2005; 13(18): 2173-2178
- URL: https://www.wjgnet.com/1009-3079/full/v13/i18/2173.htm
- DOI: https://dx.doi.org/10.11569/wcjd.v13.i18.2173
国际协调会议(ICH)制定了《ICH临床试验的统计学指导原则》ICH-E9[1]. 由于我国是协调三方之外的国家, 为了与国际接轨、掌握并实际应用这些指导原则, 有必要对其中一些常见的名词作较为详细的解释, 以澄清一些理解上的歧义. 为了更科学地设计随机化临床试验, 应当掌握不确定原则和治疗意向原则这两个重要的临床试验原则. 简单随机有其局限性即可能产生不平衡, 但可采用适当的技术加以改进. 随机化临床试验特别是大规模、多中心的临床试验存在一些不足, 临床试验的灰关联方法有望弥补. 本文对这些问题进行评述.
在数理统计和医学统计学领域中, effect一词宜按多数人习惯, 译为"效应"较妥, 而非"响应(response)."响应"是试验所观测到的结果, 是在受试对象那里所实测到的指标. 而效应常常不是直接观测到的, 是从一定数量的响应中分析出来的. 效应一般分为三类:[2]处理效应, 区组效应和误差效应. 处理效应是指当处理因素改变时引起响应的变化; 区组效应是为了对误差进行控制, 把试验的非处理因素产生的效应分解出来; 误差效应一般是随机的, 服从正态分布的. 效应按其性质可分为固定效应和随机效应. 为定量描述二者关系所假设的数学模型自然就有固定效应模型、随机效应模型和混合效应模型 三类. ICH?E9的原文中还提到"效应大小"(effect size), 文献[3]中有专门条目解释这一词组:"效应大小指由于因素引起的差别".有作者[4-6]把 effect size译作"样本含量", 从ICH?E9的上下文看, 似乎不可能是sample size之误, 在"样本含量"一节提到"效应大小", 是指主要变量引起的响应差别除以相应的标准差, 这一相对量对估算样本含量是重要的.
平衡(balance)一词在统计学中也是专业术语, 指可比较的两组或多组中各受试对象数或所作的处理数目相等; 或者说, 在不同的因素?水平组合的实验基元(cell)中各受试对象数目相同, 则称为平衡. 而均衡(homogeneity)是指一个试验组内的受试对象按照所研究的性质而言在统计上是均匀的, 一致的.
例如, 随机区组设计(randomized block design), 或称随机化完全区组设计(randomized complete block design简称 RCB):12只小鼠按体重的不同分为4个区组, 每个区组有三只, 随机分配喂以三种不同饲料. 这里每个区组内的小鼠从体重看是一致的, 称为均衡; 4个区组每个都有3种饲料, 称为完全, 本例也是平衡的; 每种饲料都喂以4种不同体重的小鼠, 称为配伍. 如果饲料多于3种, 比方说是4种, 每个区组只能安排其中的3种, 所有区组喂每种饲料的小鼠数也相同, 可以看出这里平衡有两种意义, 其一是指每区组都三只小鼠, 其二是指整个试验每种饲料都喂4个小鼠, 因此称为平衡的不完全区组设计(balanced incomplete randomized block design, 简称BIB). 如果12只小鼠的体重是均衡的, 可以完全随机地分配喂以不同饲料, 称完全随机设计(completely randomized design). 这里完全随机, 是简单随机, 有别于RCB或BIB中的区组随机; 后二者中"完全"和"不完全"是针对所有处理而言的, 同一区组内不同对象接受了所有处理, 谓之"完全", 不同区组是平衡的.
方差齐性(homogeneity of variances)意味着方差是一致的, 并不翻译成"方差均衡".方差齐性不满足 (heterogeneity of variances), 也不翻译成"方差不均衡". 对一个分布而言, 均衡分布(homogeneity of distribution)是指其变异来自随机误差, 均衡分布 (heterogeneity of distribution)是指其变异还来自系统误差[7]
国内目前出版的几十本医学统计学书籍, 几乎都认为总体; (population)是"同质观察单位的全体".国外有关的专著在说明此概念时的用语互相有很大差别, 却没有见到用过"同质"、"均衡"、"均匀"一类的词. 现把文献[8]中的定义翻译如下:"总体是特定时间内所关注的观察单位最大的集合. 如果用某一变量的数值作为观测总体中个体的尺度, 于是产生变量数值的总体."
一个实际的总体常常既有同质的一面, 又有不同质的一面, 一个总体一般都可分为不同的次级总体. 从研究总体(study population)得出统计结论, 能否或怎样推广到以后所关注的总体(目标总体)呢?ICH?E9用很大篇幅回答了这一问题. 可惜有学者[4,5]把目标总体(target population)略去不译, 把推广(generalization)有时译成"推论",有时译成"广义性".对ICH?E9的理解不仅需要把译文与原文对照, 还需研究有关参考书.
文献[9]介绍了与这两个概念有关的内容, 概括如下: 区组(blocking)是将受试对象作为样本所进行的分组或划分; 分层(stratifying)是将受试对象所在总体按某(些)特征分割为次级总体. 分组的原则一般是使一区组内处理数平衡, 有时区组内各处理数之比是个常数. 区组大小(size)或区组长度(length)是指一个区组包含多少个接受不同处理的受试单元, 预后因素(prognostic factor)是临床试验研究中有实际意义的协变量, 它可作为分层的依据. 这里需要强调的是, 在目前通用的统计学书籍中, 往往在受试对象存在不均衡的情况下才将其划分成不同的区组, 用以分解出"区组效应", 从而降低随机误差, 或者说是使随机误差更接近实际情况. 该文作者扩展了区组的概念和用法: 标以不同区组的受试对象可以是均衡的, 即实际上并不存在区组因素, 这时还要分成区组, 是为了平衡处理因素, 详见该文的有关例子.
不确定原则和治疗意向原则在一些临床试验教材中被忽略了. 在临床试验的实践中, 这两个重要原则几乎在随机化临床试验的全过程都起作用: 在入选受试者和分析试验结果时, 能避免一些偏倚; 此外, 治疗意向原则遵循Helsinki宣言, 自始至终保护受试者的权宜, 消除受试者和参加研究的医生们的种种误解和顾虑, 以保障研究数据的真实和完整. 因而应在临床试验的全过程中坚持这两条原则.
2.1.1 不确定原则: 当且仅当以下情况才能将一特定患者随机选入临床试验: 经治医生基本上不能确定试验所涉及的几个治疗组哪一个对该患者最适当.
如果因为医学的或非医学的理由, 经治医生或患者自己经过认真比较后能够确定, 试验所涉及的几个治疗中的一种安排对他(她)是不适当的, 则该患者不应入选. 这里的比较可以是空白对照, 也可以是本试验范围内或范围外的某种治疗. 每一项临床试验的实施过程中, 都有录选受试者这一重要阶段. 从研究人员方面, 要有明确的适宜性标准(E1igibility Criteria)它包括入选标准(1nclusion Criteria)和排除标准(Exclusion Criteria), 不能用一个适宜性标准来代替后二者, 因为它们互相关联. 受试者签署了知情同意书(1nformed consent)后, 才能进入试验. 有些试验在正式入选前还有一个筛选期(Run-in).
受试者面对临床试验所设计的几个治疗方案, 常常要求随机地分配给其中的一个, 随之而来的问题是: 为什么不从几个可能的方案中选最好的一个? 问题在于就目前的认识水平而言, 无法确定对该受试者的最优方案. 这就是不确定原则[10].
从上述严格数学定义的不确定原则可以看出, 它也是受试者的适宜性标准, 在录选受试者和签署知情同意书并进行随机时, 这一原则是其前提和依据. 随机和设盲是两个最常用的避免偏倚的技术方法, 但它只有在坚持这一原则时才可行和有效, 否则一位患者或医生已经认为哪个方案更有效, 却让他(她)随机成另外的方案, 势必引入偏倚.
2.1.2 治疗意向原则: "治疗意向原则"(ITT, Intention-To-Treat Principle)主张, 对一个治疗方案的效果的最好评估, 应当基于对任一对象的治疗意向(即所计划的治疗方案)的评价, 而不是评估实际所给予的治疗. 该原则首先由卸任的英国皇家统计协会主席Austin Bradford Hill提出. 该原则的推论是, 分到任一治疗组中的各对象都应当作为该组成员始终被随访、评估和分析, 不要受治疗计划执行过程中他们是否遵从的干扰. 患者被分到处理组或对照组以后, 在试验过程中, 会出现出组情况, 这种出组是临床试验的特定情况, 各组之间例数常常是不平衡的, 这种差别影响到它们之间作比较的合理性.
例如[11]将肝癌患者随机分到肝切除和介入治疗组中去. 在手术时发现有不可能完成手术的病例, 只好因不能手术而出组; 但在介入治疗组则没有这种情况. 除非出组情况非常少而无关紧要, 我们不可避免只好把患者保留在原来的各组中进行比较, 要比较和观测的是治疗的意向而不是实际的治疗. 通过此例不难看出, 肝癌患者只有在开刀以后发现病情过重者才不能完成手术, 如果从该组排除, 不仅在数目上与介入治疗组不平衡, 而且要比较的两组在病情构成上也因此改变了, 显然只有仍按原来的随机分组进行分析才合理. 这就是治疗意向原则[11].
由于不了解或不理解治疗意向原则, 在临床试验的随机和随访中会出现一些不适当的做法和误解. 且举数例.
治疗组一出现不良反应, 立即做出组处理并停止继续随访. 在告知候选对象时, 常因"一旦随机并是签署知情同意书的, 就不得退出研究"之类的语言吓走了候选对象. 须知, ITT原则是为研究者避免偏倚的, 而不是使受试者失去自主权、少报漏报不良反应, 也不是对试验分组、治疗和分析进行随意或不必要的变动, 改变本来相同的初始条件.
2.2.1 简单随机的局限: 简单随机(simple random-ization)亦称完全随机, 是指靠捣硬币或随机数表, 或计算机随机数函数进行随机化, 不加限制和干预. 这是很简单的分组和分配治疗方案的方法, 但它的局限性是可能产生不平衡.
N个受试对象, 按照简单随机分配到A和B两个处理组, 每个对象可能到任一组内的概率为P = 0.5. 分配完成后, 两组数目可能不等, 如此随机安排, 刚好两组数目相等的概率为
(1) Math 1
它可能很小. 例如, 当N = 100, 每组刚好50个受试对象的概率仅约为8%. 估价等于或大于某个特定大小的不平衡情况的概率是包含很多信息的. 利用二项分布的特性, 分到两组中每一组的期望数目为
E{NA}={NB}=NP
这一数目的方差为
(2)Var{NA}=Var{NB}=NP(1-P)
当N = 100和P = 1/2时的方差为25, 近似95%分组数目置信带(bound)为
Math 2
这样一来, 我们就会期望比60或40更为不平衡而有利于A(或B)的情况占简单随机的5%.
当我们必须考虑有影响的预后因素时, 不平衡的问题更加值得注意, 甚至当处理分配的数目是平衡的, 预后因素的分布也是不平衡的. 例如, 假定有k个独立的二值预后变量, 每个有0.5的概率是"阳性".比较时I型错误取5%, 任何一个变量是平衡的概率则是0.95, 所有k个因素都平衡的概率是0.95K. 因而, 至少发现有一个因素不平衡概率为1-0.95K, 当K = 5, 至少有一个因素在统计上显著不平衡的概率为0.23.
2.2.2 用区组改进简单随机的平衡: 区组随机, 是将随机加以约束, 使各处理的分配更加平衡, 满足研究要求. 在一个区组内包含一个预定的处理分组数目和比例. 一个区组的大小必须是处理组数的整数倍. 一区组系列是由随机数字表安排构成的, 每一区组内各处理的次序是随机安排的, 但是平衡的. 考虑两个处理组, A和B, 实现区组大小为NA+NB的有约束随机分配处理A的概率:
(3) Math 3
当在一个区组内实现了NA次分配, nA=NA, 于是再取A的概率为零, 当NB次分配完成, 则再取A的概率为1, 这是计算机产生区组安排的实用方法, 为做出每一新安排, 我们比较一随机数u与概率Pr[A], 如果u≤Pr[A]就安排A, 否则安排B, u在(0,1)内均匀分布.
如果处理数为2, A和B, 采用大小为4的区组, 则可能共有6种不同的分配(表1). 实验的分配处理的方案是由随机产生的一系列区组构成. 如果我们的试验以一个区组的一半停止, 恰巧这一半是两个A, 那么就会出现不平衡: 多出两个A来. 这说明区组引起的不平衡所产生的情况可能是区组大小的一半.
| 区组 | 处理的分配序列号 | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | A | A | A | B | B | B |
| 2 | A | B | B | B | A | A |
| 3 | B | A | B | A | B | A |
| 4 | B | B | A | A | A | B |
在小区组内可能包含的处理的排列数不大. 假设有2个处理, 区组大小是2b, 那么, 在区组内就有多种不同的分配. 如果试验严格是在一个区组的一半, 多余的分配数不超过b. 多于2个处理时用多项式系数算得可能的配置数.
实际随机化分组时, 所有区组不一定有相同的大小. 随机改变区组的长度, 两处理用2, 4, 6, ...: 三处理用3, 6, 9, ....
如果是用随机数字表, 对图1实际上是这样把随机的数字与区组的处理挂钩的:
这样一来, 随机数字如为0, 5, 2, 7, 8, 4, 3, 7...对患者安排处理: -, BABA, ABAB, -, -, BBAA, ABBA, -, .....
2.2.3 用区组和分层改进简单随机: 为了很好分析在临床上有重要意义的预后因素, 可以同时用区组和分层两种技术进行随机化. 预后因素每个组合构成一个分立的层, 每一层内再进行区组化. 在每一层内, 所分配的各处理是平衡的; 在每一处理组内, 各预后因素也是平衡的.
每个患者接受下一个处理安排是从一个特定层配置中找到的, 适合某层的她(他)入选, 各层不必以同一速率填满. 在一个有区组又分层随机方案中, 可能所有各层都填了一半, 即都有A(或B)待填. 每个处理中有b个分配, 区组大小为2b, 层数为k, 最大不平衡为kb. 换句话说, 每层都可能多出b个分配, 对2个处理, 4层, 区组大小为4, 如表2的例子, 最大不平衡数为8, 以不平衡数为8而有利一种处理或另一种处理的机会为
| 区组 | 阳性腋窝淋巴结数 | 1-3 | 4 | ||
| 年龄 | <50 | ≥50 | <50 | ≥50 | |
| 1 | B | B | A | B | |
| A | B | A | A | ||
| B | A | B | A | ||
| A | A | B | B | ||
| 2 | A | A | B | A | |
| B | A | A | B | ||
| A | B | B | B | ||
| B | B | A | A | ||
| 3 | A | B | B | B | |
| B | A | A | B | ||
| B | A | B | A | ||
| A | B | A | A | ||
| 4 | B | A | B | A | |
| B | B | A | B | ||
| A | B | A | A | ||
| A | A | B | B | ||
Math 4
而不平衡数少的机会就要大些. u,v的意义: u为每层仅停于一半的机会; v为所有k个区组具有同一分配的机会:
Math 5
如果每一个患者都是在有许多预后变量而属于特有的一层, 其结果就相当于简单随机. 这时就要少分几层, 与处理的数目要相当. 换言之, 大多数区组应该填满, 因为未填满都带来分配的不平衡. 区组太大, 就会抵消区组的平衡效果, 以一个大区组进行处理分配实质是简单随机, 除非到区组的终了附近. 例如对公式(3), 当NA和NB都很大时,对所有分配好的情况而言, Pr[A] ≈ 1/2. 区组可用于不等的分配, 例如: NA:NB:2:1, 这时区组大小应为3的倍数, 2/3分配给处理A.
每一患者进入临床研究, 须认定属于哪一层, 从相应的随机数表中得到随机的处理安排. 当有多个层时, 区组宜小一些. 虽然实际问题都可以有多个协变量, 但应抓住主要矛盾, 最好只有一个分层因素.
2.2.4 区组和分层随机的简化实例: 乳腺癌治疗研究中, 有两个预后因素较重要: 阳性淋巴结数和年龄. 年龄的重要性在于年长者其生存时间短, 这与本病无关, 而且辅助化疗也可能与年龄有关. 患者这两个预后因素作为协变量, 一般是连续变量, 但在我们这个实际情况下, 每个变量都可归结为两个值:
年龄: <50岁, ≥50岁,
阳性淋巴结数: 1-3个, 4个,
因此, 可以把乳腺癌患者按协变量分为四层:
年龄<50岁和阳性淋巴结数l-3个,
年龄<50岁和阳性淋巴结数≥4个,
年龄≥50岁和阳性淋巴结数1-3个,
年龄≥50岁和阳性淋巴结数≥4个.
在试验开始前, 准备四份互相独立的随机数字表, 每层一个, 分别按有约束随机区组安排各层, "有约束随机区组安排"与前面的叙述是一样的. 如果区组大小为4, 两个处理分别是A = L-Pam和B = placebo, 所得安排如表2.
循证医学概念的提出使大规模、多中心临床试验进入了鼎盛时期. 但大样本随机对照试验有如下缺点[12-14]: 前瞻性工作耗时长, 组织协调工作量大, 协作单位多, 质量控制难度大, 病人多, 入选标准掌握不统一, 混杂因素多, 要求随机严格, 否则可能出现偏差, 且往往是临床试验终点的单指标或少指标的评价, 忽略了综合效益的重要性, 此外还要求有足够的经费支持. 盲法安慰剂对照试验存在伦理道德问题, 它可能使受安慰剂治疗的病人延误治疗, 甚至增加不必要的死亡. 荟萃分析资料来源于数个不同的临床试验, 试验背景及质控标准易出现偏差, 而且荟萃分析是回顾性的, 它所分析的资料是历史性的, 可靠性较差, 误差往往较大. 序贯试验仅适用于单指标观察. 灰关联理论[15-17]与临床试验的实际要求相结合, 建立(1)系统多指标综合评估的临床试验设计与分析理论方法: 把既往临床试验常用的指标间对比评价发展为包含有多种内涵的"多指标系统"间的对比, 可提高对临床试验资料分析评价的效度. (2)不需要设安慰剂对照组的临床试验的灰关联方法: 把安慰剂对照改变为"理想组"对照, "理想组"是在各试验组中抽取"相对理想值"构成的, "理想组"是虚拟的, 但却来源于"临床试验的现实资料", 又是实际的, 具有可比性. 这种设计的优越性在于: 受试者避免因使用安慰剂而延误治疗, 符合伦理学要求; 作为"标准"的对照组总是最优的"理想组", 较之与没有作用的安慰剂比较, 灰关联方法希望试验方案向最优逼近, 从评价态度上更积极; 又因为"理想组"随试验背景、试验条件、受试样本等不确定因素而改变, 不可能呈现完美无缺, 所以,"理想组"作为对照的"标准"又是最现实的. (3)小样本临床试验资料的灰关联分析方法: 可在综合了多指标的基础上, 通过提高试验资料的利用效度, 达到大样本临床试验的分析效果, 从而简化试验条件, 节约人力、财力和时间等试验资源的投入. (4)评价个体化疗效的临床试验的灰关联方法: 使临床上有试验依据而不是仅仅凭经验进行个体化治疗成为可能.
把系统科学引入临床试验领域, 对个体患者的治疗效果进行评价, 临床试验结果的"非唯一解"可提供不同背景下的多种选择, 把安慰剂对照改变为"理想组"对照, 成组评价与个体化评价并举, 既考虑到临床试验结果的普遍意义, 又不偏废某些个体化的特殊问题, 这些都将赋予临床试验方法学以辩证法新思想和方法论新内容. 本文以临床试验的灰关联评估模型和对比模型为例加以说明.
①若有规定的参考效果指标集X, Xi(k)∈X为规定的参考效果指标序列, i=效果级别, 如: 显效、有效......无效. K=指标数, 那么, 对于某个指标(k), 将有i个规定的效果级别的值;
②受试对象中观察到的效果指标集表示为Y,yj(k)∈Y为第j个受试对象的观察效果指标值, k=指标数, 那么
(4) Math 6
(5) Math 7
为效果阈值个体评估的关联度. 若有一组m例受试对象, 则在效果级i上的效果阈值成组评估的关联度为:
(6) Math 8
③对应于观察效果指标yj的参考效果指标为xij ,则:
(7) Math 9
(8) Math 10
为应变效果个体评估的关联度. 若有一组m例受试对象, 则在效果级i上的应变效果成组
评估的关联度为:
(9) Math 11
④按公式(10)和(11)对指标k进行评估:
Math 12
⑤效果阈值个体评估矩阵为:
(12) Math 13
⑥应变效果评估矩阵为:
(13) Math 14
⑦对关联度的差异性进行显著性检验, 得出结论.
3.2.1方法[18,19]: 令xi∈X, xi= (xi(1), xi (2), ..., xi (n))为第i组/例的观察指标试验效果序列, i∈I, I=1, 2, ..., m; m≥2为试验组或受试对象数; k∈K, K=l, 2, ..., n; n≥3为观察指标数.
χ0=(χ0(1),χ0(2),...,χ0(n)), k∈K, K=l,2,...,n; n≥3为观察指标的理想效果序列.
若i∈I, I=1, 2, ..., m; m2为m种治疗方案所对应的试验组或受试对象数, 则为m种治疗方案的对比.
若i∈I, I=l, 2, ..., m; m2为单一治疗方案在m种不同品质的试验组或受试对象数, 则为单一治疗方案在m种不同品质的试验组或受试对象中的对比.
若i∈I, I=1, 2, ..., m; m大于2为一组m例某病受试对象数; 若令χig∈χi为其临床试验亚组序列, g∈G, G=1,2,...,l; l≥2为亚组数, 则为一组m例该病受试对象个体间对比, 并可进行亚组间综合对比.
理想效果序列中, 第k个指标的值χ0(κ)一般为遍历i的最佳效果指标值, 也可为规定的理想值. 单一治疗方案对比时, 本模型尚可根据rk作指标间对比, 但比较的结果仅是数据上的, 要结合意义分析结果; 本模型也可做个体间比较.
按公式(14)计算灰关联度, 对试验效果序列与理想效果序列进行对比分析
(14) Math 15
对关联度的差异性进行显著性检验, 得出结论.
准确理解临床试验的统计学概念, 有利于把握试验设计意图, 正确评价试验结果. 掌握并运用好不确定原则和治疗意向原则可避免一些偏倚; 简单随机的方法有产生不平衡的局限性, 这种局限可用区组随机和分层随机的技术加以解决. 随机化临床试验特别是大规模、多中心的临床试验存在一些不足, 临床试验的灰关联方法可在不设安慰剂对照时进行多指标的比较或评估, 可在小样本基础上得到较精确的结果或结论, 还可能评价个体化治疗的效果. 总之, 临床试验面临的是一大类不确定性问题, 应在一套严格的规则之下进行操作, 并不断完善其方法技术体系.
电编: 张勇 编辑:张海宁
| 1. | Anonymous. E9. Statistical Principles for Clinical Trials, September 16. 1998;. |
| 2. | Klaus Hinkelmann, Oscar Kempthorne. Design and Analysis of Experiments, Volume I. New York: John Wiley & Sons, Inc 1994; 36. |
| 3. | Curtis L Meinert. Clinical Trials Dictionary Terminology and Usage Recommendations. The Johns Hopkins Center for Clinical Trials. 1996;84. |
| 5. | 郑 筱萸. 药品临床试验管理规范. 北京: 中国医药科技出版社 2000; 318-345,607-644. |
| 7. | Grimm PR Yarnold. Reading and Understanding Multivariate Statistics. The American Psychological Association. 1995;350. |
| 8. | Wayne W Danniel. Biostatistics: a foundation for analysis in the health sciences 6th ed. New York: John Wiley & Sons, Inc 1995; 5. |
| 10. | Hennekens CH. Clinical Trials in Cardiovascular Disease. W.B. Saunders Company. 1999;24-30. |
| 11. | HILL D. The clinical and electroencephalographic diagnosis of temporal-lobe epilepsy. Scott Med J. 1961;6:258-263. [PubMed] |
| 12. | Lecoutre B, Mabika B, Derzko G. Assessment and monitoring in clinical trials when survival curves have distinct shapes: a Bayesian approach with Weibull modelling. Stat Med. 2002;21:663-674. [PubMed] [DOI] |
| 13. | Sylvester R, Van Glabbeke M, Collette L, Suciu S, Baron B, Legrand C, Gorlia T, Collins G, Coens C, Declerck L. Statistical methodology of phase III cancer clinical trials: advances and future perspectives. Eur J Cancer. 2002;38 Suppl 4:S162-S168. [PubMed] [DOI] |
| 14. | Taylor DA. Cellular cardiomyoplasty with autologous skeletal myoblasts for ischemic heart disease and heart failure. Curr Control Trials Cardiovasc Med. 2001;2:208-210. [PubMed] [DOI] |
| 15. | Tan Xuerui, Li Yuguang. Using grey relational analysis to analyze the medical data. Kybernetes. 2004;9:355. [DOI] |
| 17. | Tan Xuerui,Yang Yuhua, Deng Julong. Grey relational analysis factors in hypertensives with cardiac insufficienc. J Grey System. 1998;10:75. |
| 18. | Xu Yuchun,Tan Xuerui. Grey relational analysis on trial of trental vs anti- aggregants. J Grey System. 1997;9:365. |