Non-invasive prediction model for high-risk esophageal varices in the Chinese population

Abstract

BACKGROUND

There are two types of esophageal varices (EVs): high-risk EVs (HEVs) and low-risk EVs, and HEVs pose a greater threat to patient life than low-risk EVs. The diagnosis of EVs is mainly conducted by gastroscopy, which can cause discomfort to patients, or by non-invasive prediction models. A number of non-invasive models for predicting EVs have been reported; however, those that are based on the formula for calculation of liver and spleen volume in HEVs have not been reported.

AIM

To establish a non-invasive prediction model based on the formula for liver and spleen volume for predicting HEVs in patients with viral cirrhosis.

METHODS

Data from 86 EV patients with viral cirrhosis were collected. Actual liver and spleen volumes of the patients were determined by computed tomography, and their calculated liver and spleen volumes were calculated by standard formulas. Other imaging and biochemical data were determined. The impact of each parameter on HEVs was analyzed by univariate and multivariate analyses, the data from which were employed to establish a non-invasive prediction model. Then the established prediction model was compared with other previous prediction models. Finally, the discriminating ability, calibration ability, and clinical efficacy of the new model was verified in both the modeling group and the external validation group.

RESULTS

Data from univariate and multivariate analyses indicated that the liver-spleen volume ratio, spleen volume change rate, and aspartate aminotransferase were correlated with HEVs. These indexes were successfully used to establish the non-invasive prediction model. The comparison of the models showed that the established model could better predict HEVs compared with previous models. The discriminating ability, calibration ability, and clinical efficacy of the new model were affirmed.

CONCLUSION

The non-invasive prediction model for predicting HEVs in patients with viral cirrhosis was successfully established. The new model is reliable for predicting HEVs and has clinical applicability.

Key Words: Cirrhosis, High-risk esophageal varices, Non-invasive prediction model, Liver volume, Spleen volume

Core tip: The non-invasive prediction model for predicting high-risk esophageal varices in patients with viral cirrhosis was successfully established based on the standard formula for calculation of liver and spleen volumes. It is a novel model that has not been reported. The model was shown to be better than previous prediction models. The new model had clinical efficacy and the ability to predict high-risk esophageal varices.

INTRODUCTION

Esophageal varices (EVs) are highly common in patients with cirrhosis. The risk of rupture depends mainly on severity of liver disease, level of portal pressure, diameter of varices, red sign, and the presence or absence of coagulation abnormalities[1-4]. Diagnosis of EVs relies mainly on endoscopy, which has been described in various documentations. Among all reported recording methods, the location, diameter and risk of bleeding classification is the most commonly used method for recording EVs. This classification records location, diameter, red sign, and local condition of EVs[5].

Rupture of EVs, which can potentially occur in high-risk EVs (HEVs), is dangerous and life threatening. Current guidelines recommend that patients with HEVs should be treated with non-selective beta-blockers or endoscopic variceal ligation to reduce the risk of bleeding. Although these treatments can significantly reduce risk of esophageal variceal bleeding, because of difficulty in the early identification of HEVs in patients with cirrhosis, many of these patients have not benefited from these treatments[6,7]. The identification of HEVs is particularly important, and the currently used method is gastroscopy[8,9], a method that can conveniently be used for visual determination of diameter and red sign of EVs. Gastroscopy is considered the gold standard for the diagnosis of EVs. However, patients with cirrhosis may not receive gastroscopic examination until there is a sign of esophageal variceal bleeding, or when low-risk EVs (LEVs) progress to become HEVs. Thus, identification of HEVs is of great significance, and establishment of a non-invasive predictive model that can predict patients with HEVs should help to solve this problem.

Liver volume and spleen volume measurements are essential for patients with cirrhosis and liver transplantation[10,11]. To date, the measurement of liver and spleen volume remains a very complex process. Although computed tomography (CT) or magnetic resonance imaging (MRI) can be used to calculate the liver and spleen volume, these methods are time-consuming and laborious. To address these problems, in our previous study, we conducted Pearson correlation analysis and stepwise multiple linear regression analysis of sex, height, weight, body surface area (BSA), body mass index (BMI), and actual liver volume and actual spleen volume. The same approach has also been introduced into many other studies[12,13]. We successfully applied the BSA of the patient to establish the formulas for calculation of standard liver volume (SLV) and standard spleen volume (SSV) as follows: SLV = 858.186 × BSA - 393.349 (R² = 0.350); and SSV = 188.813 × BSA - 140.981 (R² = 0.126). These formulas were achieved using the data from 207 Chinese healthy adults and were verified using the data from another 98 healthy adults. The formulas were demonstrated to have higher accuracy and less error than other commonly used formulas[12-15].

MATERIALS AND METHODS

Patients

The data were collected from all patients with viral cirrhosis who were admitted to the Second Affiliated Hospital of Xi'an Jiaotong University (Xi’an, Shaanxi Province of China) from October 2017 to December 2018 and underwent upper abdominal CT examination. The inclusion criteria were as follows: (1) Age > 18 years; (2) Have hepatitis B viral and hepatitis C viral cirrhosis; and (3) Underwent biochemical examination, upper abdominal CT examination, and gastroscopy, and interval between examinations of no more than 3 mo. Patients with the following criteria were excluded: (1) Other types of cirrhosis such as alcoholic cirrhosis, autoimmune cirrhosis, occult cirrhosis, etc; (2) Cirrhosis patients with medium to large ascites; (3) Suspected liver tumors; (4) History of liver or spleen resection; (5) Benign diseases that may affect the size of the liver or spleen such as cysts (diameter > 1 cm; number ≥ 2); (6) Other conditions that can possibly affect the hemodynamic of portal vein or splenic vein such as thrombosis, embolism, or spongiform degeneration; (7) Other conditions that may affect liver stiffness measurement (LSM), such as BMI > 35 kg/m²; (8) Unreliable liver hardness measurement: Interquartile range/median > 0.3, success rate < 60%, or effective measurement times < 10 times; (9) Patients with viral cirrhosis but without EVs; (10) Patients with severe weight loss or malnutrition; (11) Patients with hematological disease that may affect the spleen volume; and (12) Patients with a history of bleeding from the esophagus and receiving endoscopic or surgical treatment.

A total of 86 patients, including 56 patients with HEVs and 30 patients with LEVs, who met the inclusion criteria were enrolled in this study as the modeling group. Fifty other patients who met the inclusion criteria were enrolled in the study as the external validation group. Data collection for patients in the external validation group was performed after the new model was established. The application of the new model and the collection of gastroscopy results of the external validation group are independent processes. According to the Baveno V standard, the patients were divided into HEV and non-LEV groups. Basic information of each patient such as gender, age, height, weight, and BSA was recorded. The BSA was calculated by the Mosteller formula, which is more suitable for the Chinese population, as follows: BSA= √[BW (kg) × BH (cm)/3600]. HEVs are defined by the Baveno V standard as large EVs (diameter ≥ 5 mm), small EVs (diameter < 5 mm) with red signs, or EVs for Child C patients; and LEVs are EVs that do not meet these criteria[8,16] The grading and scoring of patients with cirrhosis were performed following the Child-Pugh scoring system. This study was approved by the Ethics Committee of The Second Affiliated Hospital of Xi'an Jiaotong University. This was a retrospective study; thus, the Ethics Committee waived the requirement to obtain informed consent from the patients.

Measurement of actual liver and spleen volume

All patients underwent CT examination. The upper abdominal CT examination was performed using a multi-slice spiral CT scanner (GE 128-slice spiral CT scanner; Linux Medical System, United States) with a reconstructed layer thickness of 5 mm and at a time interval of 5 s.

The CT data from the patients were retrospectively collected. The patients’ actual liver and spleen volumes, portal vein diameter (PVD), portal vein surface area (PVSA), and spleen vein diameter (SVD), spleen long diameter (SLD) were measured using an image analysis program (Linux Imaging Workstation; Linux Medical Systems), which was performed by experienced radiologists who were unaware of the patients’ basic condition. The surface area of the liver and spleen was manually tracked at each level. The actual volume of the liver and spleen was calculated by summing the surface area of each layer and multiplying it by the layer thickness. Large blood vessels, gallbladders, and fissures were avoided throughout the entire measurement. The PVD and PVSA were measured at the midpoint of the portal vein bifurcation and portal vein confluence site. The SVD was measured at 1 cm from the portal vein and splenic vein junction site. SLD is defined as the longest radial line of the layer with the largest surface area of the spleen.

Calculation of parameters for liver and spleen

The SLV and SSV were calculated by the formulas established in our previous study as follows: (1) SLV = 858.186 × BSA - 393.349 (R² = 0.350); and (2) SSV = 188.813 × BSA - 140.981 (R² = 0.126). Other formulas included: Live r volume change rate = (CTLV - SLV)/SLV; spleen volume change rate = (CTSV - SSV)/SSV; change of liver volume = CTLV - SLV; and change of spleen volume = CTSV - SSV, where CTLV and CTSV are the actual liver volume and spleen volume calculated by CT, respectively.

Biochemical tests

All patients underwent biochemical tests, in which the data including blood routine analysis, liver function, renal function, and hepatitis detection were retrospectively collected from the patients. The blood test was performed using the XN-9000 analyzer (Xisen Meikang Medical Electronics Co. Ltd., Shanghai, China), the coagulation function test was performed using the Sysmex Co-CS-1500 system, and the liver function test was performed using the cobas 8000 analyzer (Roche Diagnostics, Mannheim, Germany).

LSM by transient elastography

All patients underwent LSM using FibroScan (Echosens, Paris, France) and FibroTouch (Haishkell Medical Technology Center, Beijing, China). The results from the transient elastography (TE) were retrospectively collected and expressed in kilopascals (kPa). For patients with more than one LSM result during the study, only the result with a lower interquartile or lower median variability was selected. Several studies have shown that FibroTouch and FibroScan can detect liver fibrosis with high accuracy and consistency, and there are no statistically significant differences between them[17,18].

Gastroscopy

EVs were examined using an Olympus electronic gastroscope (Olympus, Tokyo, Japan) by experienced doctors and were divided into three categories: (1) No EVs; (2) Small EVs (diameter < 5 mm); and (3) Large EVs (diameter ≥ 5 mm). Observation of red sign was also recorded.

The published and currently used non-invasive prediction models are as follows: Liver stiffness-spleen diameter to platelet (PLT) ratio score (LSPS) = [LSM (KPa) × SLD (cm)]/PLT (× 10⁹/L)[19]; variceal risk index (VRI) = -4.364 + 0.538 × SLD - 0.049 × PLT - 0.044 × LSM + 0.001 × (LSM × PLT)[20]; aspartate transaminase (AST) to PLT ratio index (APRI) = [AST(U/L)/AST (normal upper limit)] × 100/PLT (× 10⁹/L)[21]; AST/alanine aminotransferase ratio (AAR) = AST/ALT[21].

To evaluate the performance of the present and previous predictive models in identification of HEVs, the results from gastroscopy were used as the gold standard, and the receiver operating characteristic (ROC) curve of each model was plotted, and the area under curve (AUC) of ROC curve, sensitivity, specificity and Youden’s index were calculated. The cutoff value of the point at which the sum of sensitivity and specificity was largest was selected as the optimal cutoff value in the diagnosis of HEVs or LEVs. The validity of the prediction model was evaluated by consistency (c) statistic (corresponding to AUC), and c > 0.7 was considered effective.

Evaluation of new prediction models

The discriminating ability of the model was determined by the ROC of the model in both the modeling group and external validation group. The difference in the ROC was evaluated by the Z test. If the ROC in both groups was not different and was higher than 0.7, the discriminating ability of the model was considered good. The calibration ability of predictive models was evaluated by the Hosmer-Lemeshow test and calibration scatter plot of the two groups. Decision curve analysis (DCA) of the two groups was carried out to evaluate the clinical efficacy of the new model.

Statistical analysis

Statistical analysis was performed by SPSS 19.0 and R software (IBM SPSS, Chicago, IL, United States). Data are expressed as mean ± SD. The χ² test was employed to compare between the measured data of the HEVs and LEVs groups, and the Mann-Whitney U test was used to conduct the univariate analysis. The multivariate analysis was performed by backward WALD regression analysis. The ROC curve was obtained using SPSS 19.0. The Hosmer-Lemeshow test results, calibration plot figures, and DCA were obtained using R software. All statistical analyses were two-tailed, and P < 0.05 was considered statistically significant.

RESULTS

Characteristics of patients

Based on the endoscope result and the Baveno V standard, we divided the patients into two groups: HEV group and LEV group. Age and gender of patients in the HEV group and LEV group were not significantly different (P > 0.05), and the two groups were comparable. General characteristics of the modeling group and external validation group are shown in Tables 1 and 2.

Table 1 Comparison of general characteristics in the modeling group, n.

Parameter	Patients with HEVs, n = 56	Patients with LEVs, n = 30	All patients, n = 86	P value
Age in yr	52.93 ± 11.61	54.70 ± 12.24	53.55 ± 11.79	0.35
Male (%)	33 (58.9)	14 (46.7)	47 (54.7)	0.43
Etiology, HBV/HCV	51/5	22/8	73/13	0.47
Course of disease in mo	48.3 ± 12.1	46.7 ± 11.3	48.1 ± 11.6	0.45
Child-Pugh class, A/B/C	31/19/6	9/16/0	40/35/6	< 0.05
Diameter of EVs in mm	0.8 ± 0.2	0.3 ± 0.1	0.6 ± 0.2	< 0.01
Red sign	39	0	39	< 0.01

P < 0.05 is considered statistically significant. HEVs: High-risk esophageal varices; LEVs: Low-risk esophageal varices; HBV: Hepatitis B virus; HCV: Hepatitis C virus.

Table 2 Comparison of general characteristics in the external validation group, n.

Parameter	Patients with HEVs, n = 31	Patients with LEVs, n = 19	All patients, n = 50	P value
Age in yr	51.86 ± 10.93	55.33 ± 11.98	54.15 ± 10.38	0.37
Male (%)	18 (58.1)	10 (62.6)	28 (56.0)	0.46
Etiology, HBV/HCV	21/10	16/3	37/13	0.51
Course of disease in mo	47.6 ± 11.3	45.8 ± 12.1	46.9 ± 10.9	0.43
Child-Pugh class, A/B/C	11/18/2	7/12/0	18/30/2	< 0.05
Diameter of EVs in mm	0.8 ± 0.1	0.4 ± 0.1	0.6 ± 0.2	< 0.01
Red sign	11	0	11	< 0.01

P < 0.05 is considered statistically significant. HEVs: High-risk esophageal varices; LEVs: Low-risk esophageal varices; HBV: Hepatitis B virus; HCV; Hepatitis C virus.

Univariate analysis of HEVs

The t-test and Mann-Whitney U test were used in the univariate analysis. The results summarized in Table 3 show that PVSA, PVD, SVD, CTSV, liver-spleen volume ratio, spleen volume change rate, spleen volume change, spleen diameter, ALT, AST, and thromboplastin time of the HEV group and LEV group were significantly different (P < 0.05). By contrast, CTLV, SSV, SLV, the change rate of liver volume, liver volume change, total bilirubin, prothrombin time, PLT, and LSM of the two groups were not significantly different (P > 0.05).

Table 3 Univariate analysis of parameters of patients with high-risk esophageal varices and low-risk esophageal varices.

Parameter	Patients with HEVs, n = 56	Patients with LEVs, n = 30	P value
PVSA, mm3	227.04 ± 76.66	183.81 ± 69.10	< 0.01
PVD, mm	14.35 ± 2.64	12.67 ± 2.58	< 0.01
SVD, mm	10.08 ± 3.36	8.52 ± 2.67	0.02
CTLV, cm3	901.95 ± 219.00	935.18 ± 299.83	0.66
CTSV, cm3	917.30 ± 394.37	546.00 ± 375.35	< 0.01
Ratio of liver and spleen volume	1.18 ± 0.57	3.16 ± 5.25	< 0.01
SSV, cm3	177.03 ± 33.41	175.34 ± 29.76	0.81
SLV, cm3	1052.08 ± 151.88	1044.40 ± 135.25	0.80
Rate of change of liver volume, %	-0.14 ± 0.20	-0.10 ± 0.29	0.68
Rate of change of spleen volume, %	4.21 ± 2.11	2.06 ± 2.07	< 0.01
Change of liver volume, cm3	-150.13 ± 224.10	-109.22 ± 300.13	0.56
Change of spleen volume, cm3	740.27 ± 382.77	370.66 ± 365.27	< 0.01
Spleen diameter, cm	15.81 ± 2.67	12.67 ± 2.58	<0.01
ALT, IU/L	57.68 (15-176)	40.97 (13-88)	<0.01
AST, IU/L	36.38 (10-81)	61.26 (18-164)	<0.01
TBIL, μmol/L	27.89 (3.5-73.69)	34.12 (6-119.7)	0.59
PT in s	13.69 (9.9-24)	13.50 (9.1-18.2)	0.85
TT in s	20.44 (17.2-27.9)	20.28 (16.9-23.1)	0.01
PLT, × 109/L	57.68 (15-176)	73.77 (29-159)	0.05
LSM, kPa	20.45 (9.4-36.1)	26.8 (7.6-75)	0.26

P < 0.05 is considered statistically significant. HEVs: High-risk esophageal varices; LEVs: Low-risk esophageal varices; PVSA: Portal vein surface area; PVD: Portal vein diameter; SVD: Splenic vein diameter; CTLV: Actual liver volume measured by CT; CTSV: Actual spleen volume measured by CT; SSV: Standard spleen volume calculated by equation; SLV: Standard liver volume calculated by equation; ALT: Alanine aminotransferase; AST: Aspartate aminotransferase; TBIL: Total bilirubin; PT: Prothrombin time; TT: Thrombin time; LSM: Liver stiff measurement.

Multivariate analysis of HEVs

The parameters shown in Table 3, which show that the HEV and LEV groups were significantly different, were subjected to multivariate analysis, which was carried out using the backward WALD regression analysis. As illustrated in Table 4, the three factors related to HEVs including ratio of liver volume to spleen volume, rate of spleen volume change, and AST in patients with HEVs were significantly different (P < 0.05) from those with LEVs.

Table 4 Multivariate analysis of parameters of patients with high-risk esophageal varices and low-risk esophageal varices.

Parameter	Patients with HEVs, n = 56	Patients with LEVs, n = 30	P value
PVSA, mm3	227.04 ± 76.66	183.81 ± 69.10	0.52
PVD, mm	14.35 ± 2.64	12.67 ± 2.58	0.60
SVD, mm	10.08 ± 3.36	8.52 ± 2.67	0.20
CTSV, cm3	917.30 ± 394.37	546.00 ± 375.35	0.26
Ratio of liver and spleen volume, %	1.18 ± 0.57	3.16 ± 5.25	< 0.01
Rate of change of spleen volume, %	4.21 ± 2.11	2.06 ± 2.07	0.047
Change of spleen volume, cm3	740.27 ± 382.77	370.66 ± 365.27	0.30
Spleen diameter, cm	15.81 ± 2.67	12.67 ± 2.58	0.58
ALT, IU/L	57.68 (15-176)	40.97 (13-88)	0.71
AST, IU/L	36.38 (10-81)	61.26 (18-164)	< 0.01
TT in s	20.44 (17.2-27.9)	20.28 (16.9-23.1)	0.93

P < 0.05 is considered statistically significant. HEVs: High-risk esophageal varices; LEVs: Low-risk esophageal varices; PVSA: Portal vein surface area; PVD: Portal vein diameter; SVD: Splenic vein diameter; ALT: Alanine aminotransferase; AST: Aspartate aminotransferase; PT: Prothrombin time; TT: Thrombin time.

Establishment of non-invasive prediction model

Based on the multivariate analysis results, all parameters that were not significantly different between the two groups were eliminated, whereas those that were significantly different, which included the ratio of liver volume to spleen volume, rate of spleen volume change, and AST, were employed to establish the non-invasive predictive model. As shown in Table 5, the non-invasive prediction model was obtained as follows: ln [P/(1 - P)] = 8.342 - 2.162 × (CTLV/CTSV) - 0.314 × [(CTSV - SSV)/SSV] – 0.07 × AST. The ratio of liver volume to spleen volume, the rate of spleen volume change, and the AST were negatively associated with HEVs.

Table 5 Parameters used to establish the non-invasive prediction model.

Parameter	B	SE	Wals	df	Sig	Exp (B)	95%CI of exp (B)
Ratio of liver and spleen volume	-2.162	0.683	10.028	1	0.002	0.115	0.030-0.439
Rate of spleen volume change	-0.314	0.246	1.619	1	0.203	0.731	0.451-1.185
AST	-0.070	0.020	12.672	1	0.000	0.933	0.898-0.969
Constant	8.342	2.413	11.946	1	0.001	4194.879

AST: Aspartate aminotransferase; df: Degree of freedom; CI: Confidence interval.

Comparison of prediction models

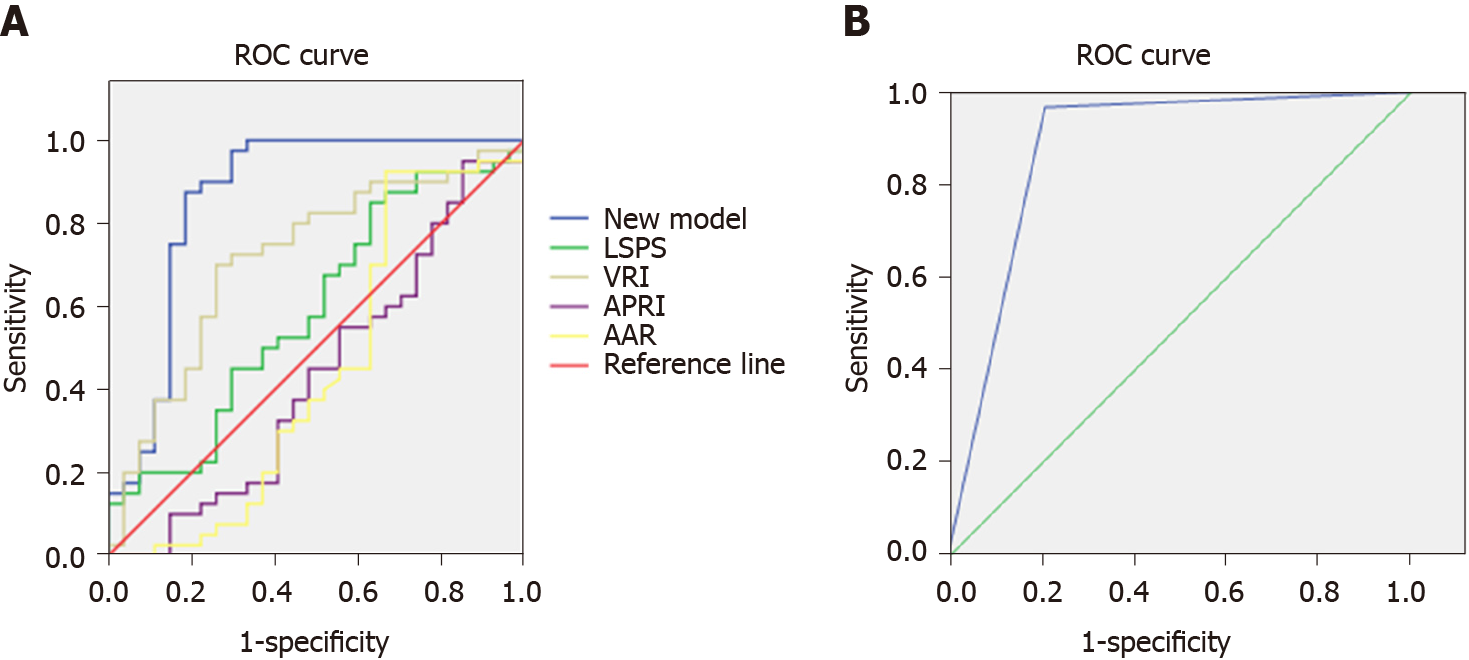
The non-invasive predictive model for predicting HEVs in patients with viral cirrhosis established in the present study was compared with other previously reported models, namely LSPS, VRI, APRI, and AAR, which have been widely used for assessing EVs in patients with cirrhosis. Sensitivity, specificity, and AUC of the four indicators and of the established non-invasive prediction model for the modeling group were calculated. The cutoff value of the non-invasive prediction model was defined based on the maximum value of the sum of sensitivity and specificity. When the P value calculated by the established formula was larger than the cutoff value, the patients were considered to have HEVs. The results depicted in Figure 1A and Table 6 show that the AUC of the present model was 0.865, whereas that of the ROC curves of LSPS, VRI, APRI, and AAR were 0.591, 0.717, 0.431, and 0.445, respectively. A model with an AUC of higher than 0.7 was considered to have good discriminating ability. The higher the AUC, the better the discriminating ability of the model.

Figure 1 Area under the curve of various models in predicting high-risk esophageal varices of patients. A: Modeling group; B: External validation group. The area under the curve of the new model in predicting high-risk esophageal varices of patients was 0.865 in the modeling group, which was higher than that of liver stiffness-spleen diameter to platelet ratio score, variceal risk index, aspartate transaminase to platelet ratio index, and aspartate transaminase /alanine aminotransferase ratio; and it was 0.879 in the external validation group. ROC: Receiver operating characteristic.

Table 6 Comparison of various parameters of each model.

	Area	SE	Sig	95%CI of exp (B)	Sensitivity	Specificity	Youden’s index
The new model	0.865	0.054	0.000	0.759-0.970	0.91	0.80	0.71
LSPS	0.591	0.072	0.210	0.450-0.732	0.85	0.37	0.22
VRI	0.717	0.065	0.003	0.589-0.844	0.70	0.74	0.44
APRI	0.431	0.074	0.344	0.285-0.577	0.95	0.15	0.10
AAR	0.445	0.080	0.447	0.288-0.601	0.93	0.33	0.26

CI: Confidence interval.

Comparison of accuracy of the models

Accuracy, positive predictive value, and negative predictive value of all models (non-invasive predictive model, and LSPS, VRI, APRI, and AAR models) were calculated in all 86 patients enrolled in the modeling group. As shown in Table 7, the present non-invasive prediction model had high accuracy of 84.9% and high positive predictive value of 96.4%. The accuracy and the positive predictive value indicate the possibility of correctly diagnosing HEVs: the higher their values, the more likely the diagnosis is correct.

Table 7 Comparison of accuracy of each model in predicting high-risk esophageal varices of patients in the modeling group.

	Accuracy, %	Positive predictive value, %	Negative predictive value, %	Cutoff value
New model	84.9	96.4	63.3	0.5713638
LSPS	82.1	85.0	37.0	3.0852585
VRI	70.1	70.0	74.1	0.52695
APRI	67.4	96.4	13.3	0.5671263
AAR	68.6	89.3	30	0.9861111

LSPS: Liver stiffness-spleen diameter to platelet ratio score; VRI: Variceal risk index; APRI: Aspartate transaminase to platelet ratio index; AAR: Aspartate transaminase/alanine aminotransferase ratio.

Evaluation of discriminating ability of the new model

To evaluate the discriminating ability of the new model, we generated ROC curves of the external validation group using the new models and compared between the AUC curve of the modeling group and the external validation group using the Z test. The results showed that the AUC of the external validation group was 0.879. The Z test result also showed that the P value was 0.17, which indicates that the modeling group and the external validation group were not significantly different. This also indicates that the discriminating ability of the new prediction model was similar for both the external verification group and the modeling group. The ROC curve of external validation group is shown in Figure 1B.

Evaluation of calibration ability of the new model

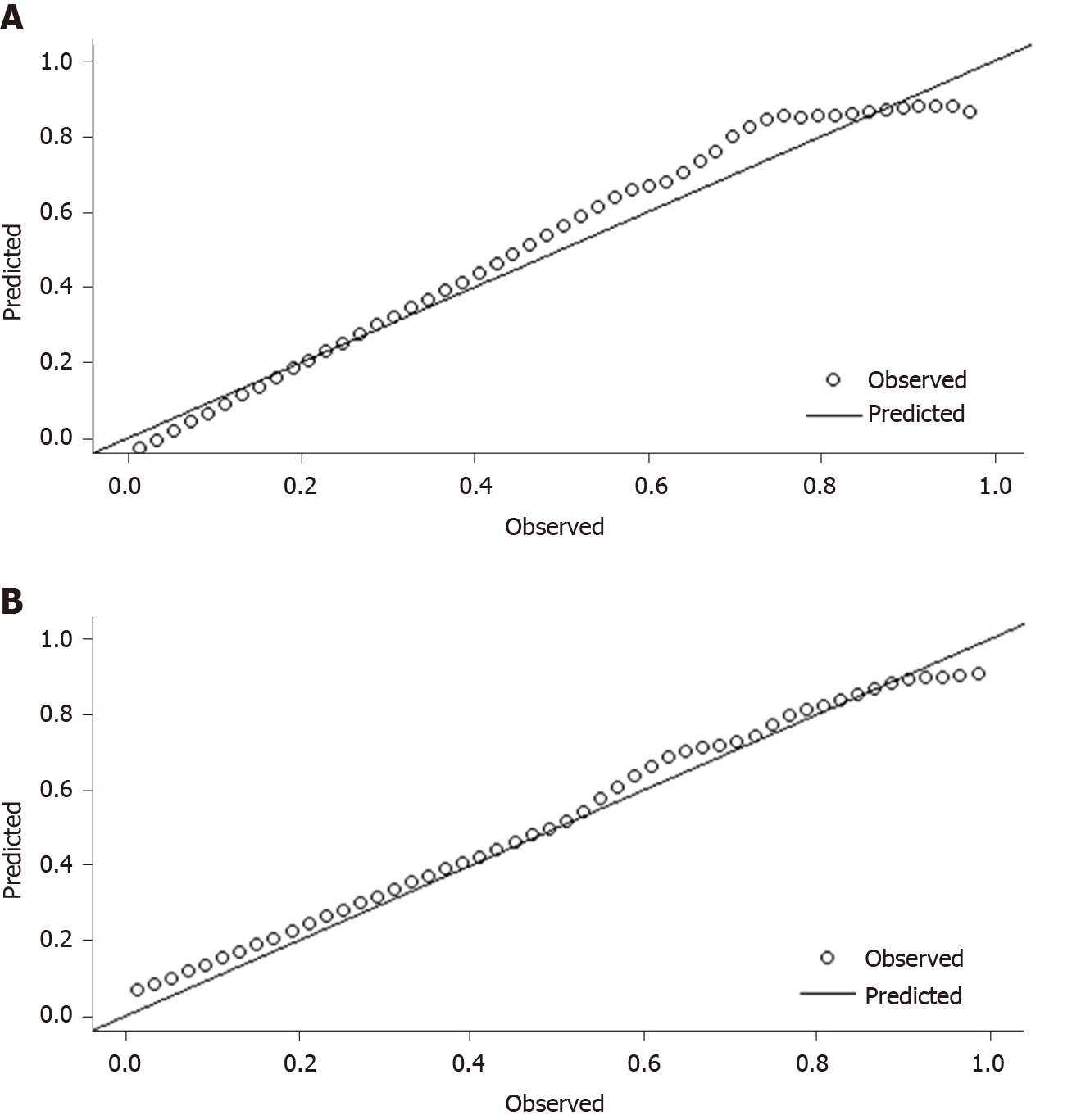
To evaluate the calibration ability of the new model, we used the Hosmer-Lemeshow test to calculate the χ² for the modeling group and the external validation group. The results showed that the χ² of the modeling group was 4.86, and that of the external validation group was 4.69; their P values were 0.746 and 0.790, respectively. The P values of both groups were higher than 0.05, indicating that the new model accurately predicted HEVs in both groups. The calibration scatter plots of both groups are shown in Figure 2. According to the plots, all scattered points fluctuated around the reference line without significant deviation, which was due to the fact that the P values of both groups were higher than 0.05 and there was no statistical difference between the two groups. This result suggests that using the new model, the predicted HEV patients were in good agreement with the actual HEV patients.

Figure 2 Calibration scatter plot of data of patients. A: Modeling group; B: External validation group. In predicting patients in the modeling group and external validation group, the scattered points fluctuated around the reference line without significant deviations.

Evaluation of clinical efficacy of the new model

We used the DCA to evaluate the clinical efficacy of the new model. The DCA was drawn using the predicted probability of the model group and the external validation group and the actual occurrence of HEVs. The predicted probability of the model group was represented by P_in and that of the external validation group was represented by P_out. The DCA of the two groups are shown in Figure 3. In the DCA curve, the black line indicated that in extreme cases, the new model predicted that there were no HEVs in all patients with viral cirrhosis and the clinical net benefit was 0. The gray line, which had a negative slope and was the clinical net benefit, indicated that in extreme cases, the new model predicted that there were HEVs in all patients with viral cirrhosis. The red line was the DCA of the new model. According to the DCA curves, the red line was higher than the black and gray lines, suggesting that both groups of patients could benefit from the new model when it is applied to two cohorts. It also suggests that the new model has clinical efficacy.

Figure 3 Adjusted decision curve analysis of data of patients. A: Modeling group; B: External validation group. The black line indicates that in extreme cases, the new model predicted that there were no high-risk esophageal varices in all patients with viral cirrhosis, and the clinical net benefit was 0. The gray curve indicates that in extreme cases, the new model predicts there are high-risk esophageal varices in all patients with viral cirrhosis, the clinical net benefit is the negative slope. The red line indicates that the new model has a clinical net benefit. The red line is higher than the black and gray lines, indicating that patients in the modeling group can benefit from the new model.

DISCUSSION

In China, there are a large number of patients with liver cirrhosis due to the high infection rates of hepatitis B and C[22,23]. Although gastroscopy is the gold standard diagnosis technique for EVs, its procedure is invasive, and thus can cause discomfort to patients. Painless gastroscopy can significantly reduce the discomfort, and most gastroscopy in China is performed without anesthesia. The risk of bleeding in patients with EVs is different, and according to the Baveno V standard, EVs are divided into high bleeding risk EVs and low bleeding risk EVs. For patients with HEVs, taking preventive measures early significantly reduces the risk of esophageal varices bleeding. In China, many patients with liver cirrhosis do not receive the first gastroscopy until the esophageal varices rupture and bleed. Thus, it is highly important to accurately identify patients at high risk of bleeding caused by esophageal varices.

Other than gastroscopy, CT or MRI can also be used to predict the HEVs, and thus are often used to make preliminary judgments about the presence of EVs[24]. However, these two techniques cannot visually observe the red sign, making it difficult to correctly diagnose HEVs. There are many non-invasive models that can be used to predict HEVs, and the most commonly used models include LSPS, VRI, APRI, and AAR. The indexes used in these models include AST, ALT, PLT, PLD, and LSM. According to various studies, these models have proven to be effective in predicting HEVs[19-21]. The liver and spleen volume ratio is also an effective index that can be used to establish a non-invasive model to predict the hepatic vein pressure gradient[25]. Although many studies have reported the formula for calculating liver volume, few have reported its clinical application. Unlike these models, in this study, we used the volume calculation formulas established in previous studies to calculate the standard liver and spleen volumes, and used CT data to calculate the actual liver and spleen volumes. The differences between the calculated volumes and the actual volumes were considered the pathological change. Change rates of volume and other indexes related to liver and spleen volume were adopted to establish the non-invasive model for predicting HEVs. This approach has not been reported.

We successfully constructed a non-invasive prediction model that can predict HEVs, as follows: ln [P/(1 - P)] = 8.342 - 2.162 ×(CTLV/CTSV) - 0.314 × [(CTSV - SSV)/SSV] - 0.07 × AST. We selected the cutoff value, the point at which the sum of sensitivity and specificity was largest, as the optimal cutoff value, which was 0.571. When the value of P in the model was higher than the optimal value, HEVs were considered present. In validation of the new model, we compared AUC, sensitivity, specificity, Youden’s index, accuracy, positive predictive value, and negative predictive value of the new model with those of LSPS, VRI, APRI, and AAR in 86 cirrhosis patients with EVs. The new model had an AUC of 0.865, a Youden’s index of 0.71, an accuracy of 84.9%, and a positive predictive value of 96.4%. The results obtained from the new model were better than those obtained from LSPS, VRI, APRI, and AAR. High AUC (> 0.7) and Youden’s index indicated that the model can accurately predict HEVs. The positive predictive value was an important index that reflected the model’s ability to make a positive diagnosis of HEVs, which was the primary aim of this research: The higher the positive predictive value, the greater the probability of a positive diagnosis. In summary, we conclude that the new model can better predict HEVs compared to other previously reported models.

We further evaluated the discriminating ability, calibration ability, and clinical efficacy of the new model in predicting HEVs in both the modeling group and the external validation group. The discriminating ability of the model was determined based on the AUC of ROC curve. According to the results, the AUC of the model was higher than 0.8 in the two groups, indicating that the model had good discrimination ability (the AUC between 0.7 to 0.9 indicated that the model had good discrimination ability). The calibration ability of the model was analyzed by the Hosmer-Lemeshow test and the calibration scatter plot. In prediction of patients in both groups, the P values of the model were higher than 0.05, and the scattered points fluctuated around the reference line without significant deviation, indicating that the model had good calibration ability. The DCA can be used to evaluate the clinical efficacy of the model[26,27]: The model was considered to have clinical efficacy only when its DCA was higher than the extreme line. According to the DCA figures, the DCA of the new model was higher than the extreme line, indicating that the new model had good clinical efficacy. Therefore, the new model can accurately predict HEVs and has clinical application value.

Taken together, we successfully developed a non-invasive predictive model that can predict HEVs in patients with viral cirrhosis using the liver and spleen volume calculation formulas, which has not been reported. The model was compared with other previous models including LSPS, VRI, APRI and AAR. Comparisons of AUC of ROC curve, sensitivity, specificity, accuracy, positive predictive value, and negative predictive value of each model showed that the established non-invasive prediction model better identified patients with HEVs than other models. Evaluation of the new model showed that it had high discriminative ability, calibration ability, and clinical efficacy. Moreover, the subjects included in this study were patients with viral cirrhosis; this can minimize the bias of the results while providing good consistency. This research had some limitations, such as the small sample size. In addition, the application of the model relied only on CT, a technique that can cause harm to patients. In China, CT is used for routine examination of patients with cirrhosis, with the aim of excluding the liver tumor. Other countries may use different techniques. All patients enrolled in this study were Chinese; thus, it remains unclear whether the model is applicable to patients in other ethnic groups. Moreover, the change in liver and spleen volume in viral cirrhosis patients was different from that in alcohol cirrhosis patients, and the new model can only be used in viral cirrhosis patients. These limitations may affect the promotion and application of the new model.

ARTICLE HIGHLIGHTS

Research background

Several models for predicting high-risk esophageal varices (HEVs) have been reported; however, models that are based on liver and spleen volume calculation formula in HEVs have not been reported.

Research motivation

HEVs are EVs that have a high risk of bleeding, and the establishment of a non-invasive predictive model will be useful for the early identification of HEVs. These patients will benefit if necessary measures are taken in a timely manner.

Research objectives

This present study established a non-invasive prediction model based on the liver and spleen volume calculation formula for predicting HEVs in patients with viral cirrhosis.

Research methods

Eighty-six EVs patients with viral cirrhosis, from October 2017 to December 2018, were included at the Second Affiliated Hospital of Xi’an Jiaotong University. By reviewing the medical records, required data were collected for. The impact of each parameter on HEVs was analyzed by univariate and multivariate analyses, the data from which were employed to establish a non-invasive prediction model. Then the established prediction model was compared with LSPS, VRI, APRI, and AAR. The discriminating ability, calibration ability, and clinical efficacy of the established model were verified in both the modeling group and the external validation group.

Research results

After univariate and multivariate analysis, liver-spleen volume ratio, spleen volume change rate, and aspartate aminotransferase were successfully used to establish the non-invasive prediction model for HEVs. The new model could better predict HEVs compared with LSPS, VRI, APRI, and AAR. The discriminating ability, calibration ability, and clinical efficacy of the new model were verified.

Research conclusions

The non-invasive prediction model for predicting HEVs is a reliable model for predicting HEVs and has clinical applicability.

Research perspectives

The predictive value of the new model needs to be confirmed in a large number of virus cirrhosis patients with EVs. Predictive models with high accuracy need to be established taking into account the limitations of the new model.