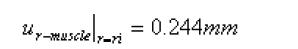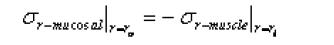The oesophageal zero-stress state and mucosal folding from a GIOME perspective

Abstract

The oesophagus is a cylindrical organ with a collapsed lumen and mucosal folds. The mucosal folding may serve to advance the function of the oesophagus, i.e. the folds have a major influence on the flow of air and bolus through the oesophagus. Experimental studies have demonstrated oesophageal mucosal folds in the no-load state. This indicates that mucosal buckling must be considered in the analysis of the mechanical reference state since the material stiffness drops dramatically after tissue collapse. Most previous work on the oesophageal zero-stress state and mucosal folding has been experimental. However, numerical analysis offers a promising alternative approach, with the additional ability to predict the mucosal buckling behaviour and to calculate the regional stress and strain in complex structures. A numerical model used for describing the mechanical behaviour of the mucosal-folded, three-layered, two-dimensional oesophageal model is reviewed. GIOME models can be used in the future to predict the tissue function physiologically and pathologically.

Key Words: Oesophagus; Finite element analysis; Zero-stress state; Buckling

EXPERIMENTAL AND MODELING APPROACHES TO THE ZERO-STRESS STATE AND MUCOSAL BUCKLING

New computational models for describing the gastro-intestinal (GI) tract mechanical behaviour precisely are a GIOME approach for bioengineering tissue modelling. The zero-stress state provides a standardized reference state for describing the mechanical response to external loading[1-4]. A large number of studies have been published on the zero-stress state of the cardiovascular and GI systems. The zero-stress state in soft biological tissues can be obtained by an experiment where tissue rings are cut radically, opening up into sectors. The angle subtended by the open ring, referred to as the opening angle, is used as a measure of the residual stress present in the intact ring of the tissue[2]. However, recent studies on multi-layered organs such as blood vessels and the GI tract indicate that the zero-stress state differs between layers and that a stress jump exists between the layers[5-11]. Thus, the true stress-free configuration for a multi-layered model is at least a twice cut tissue ring; one circumferential cut for layer separation and one radial cut in each layer to generate a true stress-free state.

Longitudinal mucosal folds exist throughout the length of the oesophagus. It was originally believed that the folding was caused by the contraction of the muscle layer in an in vivo state[12]. However, the folds appear even at the no-load state[5]. Hence, additional tension caused by the compressed mucosa-submucosal layer exists in the muscle layer at the no-load state. Furthermore, the mucosal layer is not perfectly elastic, its circumferential length cannot decrease to zero, thus the tension in the muscle layer will collapse the mucosal layer[12]. Therefore, the buckling feature of the oesophagus must be accounted for in a reference state analysis since the material stiffness drops dramatically after tissue collapse.

In the airways it has been shown that the number of folds depends on the luminal radius, mucosal thickness and on the elasticity of the mucosal layer[13,14]. However, since only experimental work has been done on oesophageal mucosal folding, no detailed information exists on relations between the stress-strain and buckling of the oesophageal mucosa. A numerical model used for buckling analysis in a three-layered (the epithelium, the muscularis mucosal-submucosal (MMS) and the muscle), two dimensional oesophageal model has been generated. Such bioengineering GIOME models can be used in the future to predict the tissue function both physiologically and pathologically.

NUMERICAL MODELING

Previous zero-stress state analysis has been based on data from rat, rabbit and guinea pig[1,5,6,9,10,15]. In yet unpublished studies, the zero-stress morphology data were obtained from five male 300 g Wistar rats. Geometric models for the oesophageal muscle and mucosal-submucosal layer were generated based on the morphology of the separated oesophagus at the zero-stress state[5,6,15]. The oesophageal passive mechanical properties were tested from the two other Wistar rats by using a tensile test machine[16,17].

Geometric models

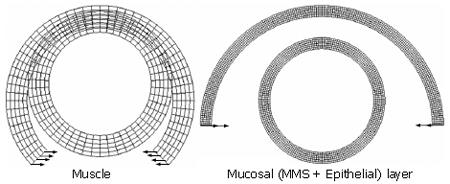
Previous studies have shown that the muscle layer at the no-load state is stretched while the mucosal layer (the epithelial layer + the MMS layer) is compressed (Table 1)[5,6,9,18]. Tensile and radial stresses induced by muscle layer stretch existed at the interface between the muscle layer and the mucosal layer. The radial stress is the balance stress that acts on the mucosal layer to produce the folds. For simulating the three-layered, mucosal folded oesophageal wall, the analysis was divided into two steps. The first step was to simulate the separated muscle layer and mucosal layer from an opening sector to the closed rings. The configurations for the opening sectors and the closed ring are illustrated in Figure 1. The second step was to stretch the muscle layer according to the experimental morphological measurement and to compress the mucosal layer by using the pressure that acted on the interface between the muscle and the mucosal layer (the pressure was equal to the radial stretch stress at the inner surface of the muscle layer).

Table 1 The average geometry data of the three-layered oesophagus.

	Openingangle (TS) (degree)	Inner radius(TS) (mm)	Thickness(TS) (mm)	Inner radius(NS) (mm)	Interfaceradius (NS) (mm)
Muscle	47	1.28	0.37	0.95
MMS	91	2.21	0.15	1.23	1.19
Epithelial	91	2.14	0.07	1.16

MMS: Muscularis mucosae-Submucosa; TS: true zero-stress state; NS: no-load state.

Figure 1 The configurations of the separated muscle (left) and the mucosal (right) layer at the zero-stress state (open sectors) and the no-load state (closed circular rings). The no-load state was obtained by forcing the opening sector to be closed using a pure bending deformation. The pure bending loads are indicted by arrows. The numerical model was conducted by using the ABAQUS software.

Mechanical properties

The mechanical properties of the muscle and mucosal-submucosal layers were obtained based on the un-axialtensile test and circumferential planar test on each layers. The tests were conducted in a tensile test machine consisting of an organ bath, motion table, force transducer and electronics[15,16]. The force and displacement curves were obtained simultaneously during the tensile test. Hence, the uni-axial stress-strain can be calculated.

Stress-strain calculation

The stress and strain calculation for the circumferential uni-axial tensile test and planar test:

Stretch ratio: λ = (C/C₀) (1)

Lagrangian Stress T = F/(W_ring× h × 2) (2)

where C and C₀ are the length between the centre of the two rods before and during deformation, F is the recorded force. C, h, and W_ring refer to the circumference, thickness and width of the rings, respectively.

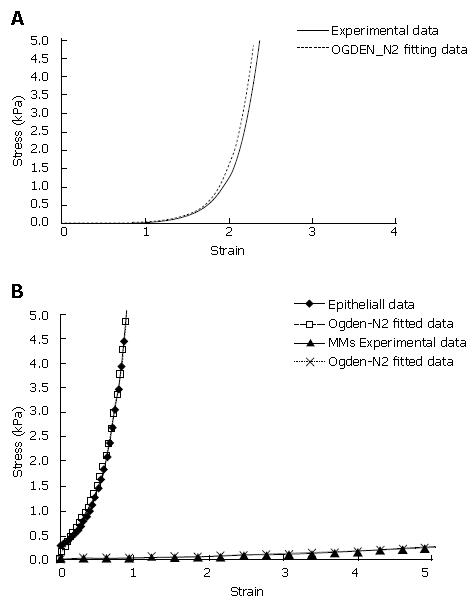
The circumferential stress-strain curves for both the muscle and mucosal layer show an exponential, large deformation pattern. Consequently, the muscle layer and the mucosal layer must be modelled as a hyperelastic material by using 2nd Ogden strain energy functions[19] (Figure 2A). To the best of our knowledge, data on the material properties do not exist on the separated MMS and epithelial layer. Thus, it was assumed that the stress-strain curve obtained from the separated mucosa-submucosal layer mainly determined the mechanical properties of the epithelial layer. The stress-strain curve of the MMS layer was assumed to have a similar pattern as the epithelial layer but it was about one order softer than the epithelial layer. Hence, for achieving the same stress level, the submucosal layer will be deformed about ten times more than the epithelial layer) (Figure 2B).

Figure 2 Circumferential experimental and curvefitted stress-strain curves for the muscle (A) and mucosal (B) layers. The curves were fitted by using the Ogden 2nd order strain energy function. The stress-strain curve of the epithelial layer was tested from the mucosal-submucosal layer while the stress strain curve of the MMS layer was assumed to have a similar pattern as the epithelial layer with the magnitude about one order softer than the epithelial layer. For the circumferential uni-axial test and the circumferential planar test the separated muscle and mucosal-submucosal rings were fixed in two L shape rods, one end of the L shape rod was connected to a cannula. The cannulas were connected to rods that could be moved at controlled velocities by a motor. One of the rods was attached to a force transducer. The distance between the rods was adjusted manually to the in vitro length of the strips (reference length). The force (F) was recorded online by a Labview program.

Boundary conditions

The boundary conditions for the first step are: The separated muscle and mucosal opening sectors were forced to be closed by using a pure bending deformation (Figure 1).

The boundary conditions for the second step were defined based on the morphological data in Table 1:

For the muscle layer

Math 3

Math 3 Math(A3).

for the mucosal layer

Math 4

Math 4 Math(A4).

u is displacement in the radial direction, σ_r is the radial stress and the substitute r₀ and r_i are the inner surface of the muscle and the outer surface of the mucosal layer.

Buckling analysis and mesh independent test

The first step for the buckling analysis was to compute the buckling mode or shape by using a linearized buckling analysis. The preferred buckling mode according to the experimental images was introduced into the numerical model by using imperfections. A nonlinear static analysis was then applied to generate quantitative relationships between the external compression stress and the associated internal deformations and stress distributions for an imperfect structure.

The mesh independent test was processed on the double amount of the meshes each time for looking for the convergence. The mesh was considered independent when the displacement errors between the two analyses were less than 5%.

LAYERED BUCKLING MODELING

Circumferential stress and strain in the separated layers after bending

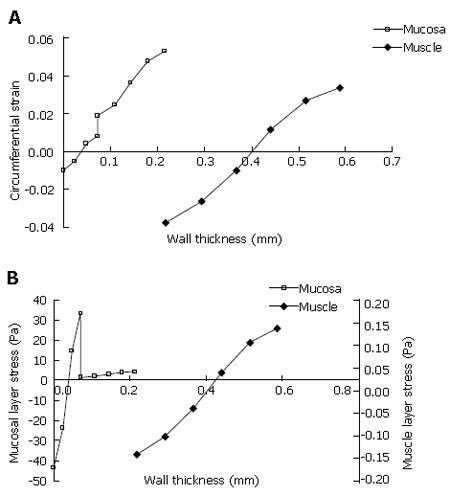
For the strain analysis, the numerical model presented similar result as the previous experimental studies, i.e. the inner wall was in compression and the outer wall was in tension for both the muscle and mucosal layer (Figure 3A). However, the strain distribution through the wall can be further advanced using the numerical model. The neutral surface (with zero strain) was located 50% and 18% from the inner side of the muscle and mucosal layer. The residual stress analysis in most of the previous zero-stress study was neglected due to the lack of the material properties. The numerical model shows the compressive and tensile stresses in the epithelial layer were significantly higher than that in the muscle layer, which is consistent with the stiffer tissue material in the epithelial layer (Figure 3B).

Figure 3 The circumferential strain (A) and stress (B) distribution throughout the muscle and mucosal (MMS + epithelial) layers after the separated muscle and mucosal layer sectors were closed. The strain and stress jump occurred at the interface between the epithelial and MMS layer.

Residual stress and strain distribution at the no-load state

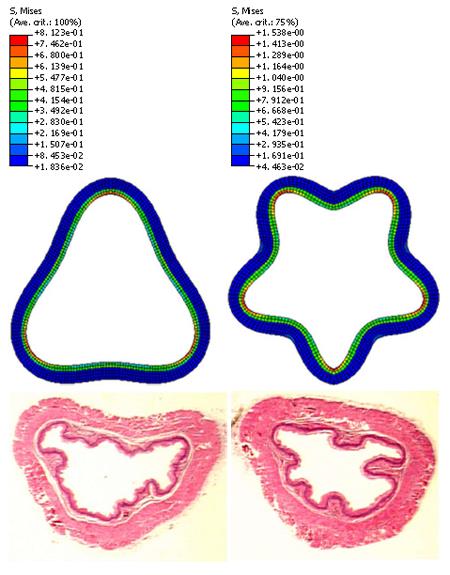
The muscle layer at the no-load state was fully stretched (Figure 4A). The radial stress at the interface between the inner muscle surface and the outer MMS surface was 0.26 Pa (Figure 4B). Buckling mode three and five were used for imperfection in the buckling analysis according to the experimental observation (Figure 5). The stress distributions after buckling are heterogeneous. The region with the lowest stress was found in the MMS region (blue colour in Figure 5) due to the softer stiffness. The highest stress region was located at the bending place in the epithelial layer (Figure 5).

Figure 4 Circumferential residual strain (A) and residual Mises stress (B) distribution in the muscle layer at the no-load state. Strain was positive throughout the muscle wall.

Figure 5 Residual stress of the mucosal layer in a three folds model (Top, left) and five folds model (Top, right). The morphological oesophageal images indicated that the folds numbers are between three (bottom, left) and five (bottom, right) at the no-load state.

SUMMARY AND PERSPECTIVES

Buckling in the oesophagus

Some materials are strong in tension but offer little resistance to deformation when uni-axially compressed. The large deformation in compression is called buckling. Buckling is a common phenomenon in organs. Tissue is in tension when the stretch ratio > 1 and in compression when the stretch ratio < 1. Tissue buckling occurs when the stretch ratio < 1[2]. The oesophagus uses buckling to advance its normal function. Without food in the lumen, a small tension in the circumferential muscle is sufficient to cause large buckling to the mucosa and submucosa. Qualitatively, the course of fold formation can be as follows: As the oesophagus contracts, no folds need to form until the radius of the hollow organ is reduced beyond the ability of the mucosal elasticity to take up the slack. Thereafter, the surface is thrown into folds as the increasingly redundant lining membrane adjusts to the diminishing circumference of the lumen. Finally, when the tone of the contracted organ reduces the area of the lumen to zero, the maximum number of folds will be present[12].

Advantage of the numerical model

Mucosal folds in previous multi-layered oesophageal models were either neglected[6]or simulated as the irregular boundary[5]. This paper points out that the wall stiffness of the inner layer dropped dramatically after the collapse. Thus, the buckling appeared under a very small critical buckling stress at the no-load state. This phenomenon is consistent with in vitro experiments showing that rabbit oesophageal mucosal folds disappear at the luminal pressure of 1 cm H₂O (unpublished data). It is thus suggested that the extended inner mucosal layer must be used as a reference state for tension or stress calculation during in vivo ultrasound studies, for example.

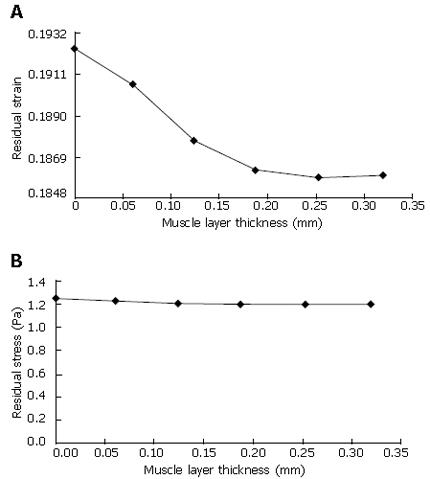
The stress level in the modelling study is significantly smaller than the previous layered oesophageal numerical studies[11]. One reason could be that a different stress-strain relationship was used. Another reason is that the buckling feature was neglected in the previous residual stress and strain analysis. Hence, the no-load state in the previous study was simplified. The residual stress and residual strain were calculated based on the configuration difference between the zero-stress state and the no-load state[1,2,4]. Thus, a precise description of the zero-stress state and the no-load state of the layered oesophagus is necessary for accurate estimation of the residual stress and residual strain.

Limitations of the current model

Since 2-D analysis was done the assumption of plain strain implies no deformation in the axial direction. The external loading in the model, simulating the effect of smooth muscle constriction, consisted entirely of radial and circumferential stresses since only the separated zero stress state and the no-load state was investigated. The in vivo axial stretch ratio of the oesophagus is about 150%. Consequently, it is expected that the muscle wall will be compressed even more and the number and the size of the folds may be different. An obvious simplification of the anatomy of the oesophagus was used in this model, i.e. that the buckles formed in a symmetric pattern. The non-circular oesophageal geometry is expected to influence the folding pattern (Figure 5, bottom).The mechanical properties of the MMS-epithelial layer were assumed from the measured mucosal-submucosal layer since no data exist.

Clinical perspective and future GIOME studies

The buckling behaviour has been studied previously on the upper GI tract and the airway system[11-14,20,21]. It has been found that the folds size and number are related to the mucosal thickness and the material stiffness. Inflammation, edema, lymphoma, and Menitrier’s disease all thicken the mucosa; they are all associated with a reduction in the number and an increase in the size of the folds[12]. Longitudinal folding exists along the inner surface of the oesophagus, and possibly occluding the internal lumen. This has a major influence on the flow through the lumen. The nature of this folding and the resistance to narrowing are functions of the composition, geometry and structural properties of the various oesophageal wall components. Hence, buckling analysis can be further used clinically for predicting the tissue remodelling physiologically and pathologically. This study shows that bioengineering models in the future of the GIOME can provide important new knowledge on tissue function.