Towards a multiscale model of colorectal cancer

Figure 1 Normal colonic mucosa. The normal colonic mucosa consists of crypts (lined with epithelium) embedded within a connective tissue stroma. The mucosa rests on a layer of smooth muscle, called the muscularis mucosae, below, which is a loose connective tissue layer, called the submucosa. The epithelium consists of a number of different cell types including goblet cells (containing mucin), enterocytes and neuroendocrine cells (which secrete hormones). The crypts are enveloped by a sheath of myofibroblasts that are separated from the epithelium by basement membrane. The stroma contains a number of different cell types including macrophages, fibroblasts and lymphoid cells. The crypt is a dynamic structure that turns over every 3-6 d. The base of the crypts contains the stem cells that are thought to give rise to transit amplifying cells. The cells migrate up the crypt and undergo differentiation along the way. The goblet cells secrete mucin into the crypt and intestinal lumen and the surface epithelium usually contains few goblet cells. Upon reaching the surface, the cells undergo apoptosis and are shed into the lumen. The migration along the crypt by the epithelial cells is accompanied by a similar migration of myofibroblasts. The microenvironment is thought to change along the crypt axis and this is thought to give environmental cues for induction of maturation and inhibition of proliferation.

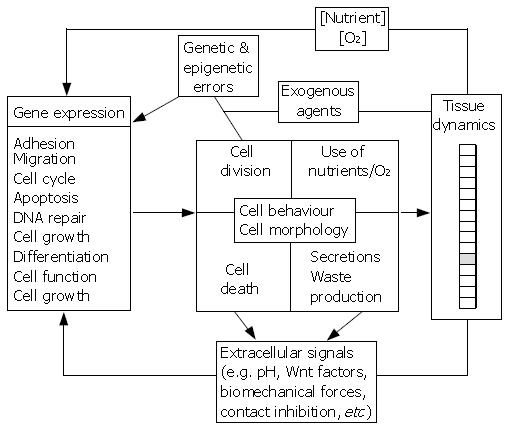
Figure 2 Prototype multiscale model of the gut. Subcellular, cellular and tissue elements are represented in black, grey and white boxes, respectively. The schematic shows possible interactions and feed-back loops coupling the different levels of organisation and illustrates the complexity of the biological system. An additional challenge in building such multiscale models is coupling phenomena that act on very short time scales (e.g. the diffusion of metabolites and signalling molecules in the extracellular medium) with processes that occur on longer time scales (e.g. tumour growth).

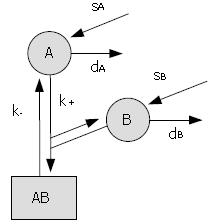
Figure 3 Example of a simple kinetic model. The proteins A and B undergo normal protein turnover (s = synthesis rates, d = degradation rates) and associate to form a protein complex, AB (k₊ = assembly rate, k_- = dissociation rate). The behaviour of the system is captured by the following system of ordinary differential equations: d [A]/dt = s_A - k₊ [A] [B] + k_- [AB] - d_A [A]; d [B]/dt = s_B - k₊ [A] [B] + k_- [AB] - d_B [B]; d [AB]/dt = k₊ [A] [B] - k_- [AB]; with initial conditions [A] (0) = A₀, [B] (0) = B₀ and [AB] (0) = 0. It can be shown that, eventually, the components stabilise at levels given by: [A] = s_A/d_A; [B] = s_B/d_B, and [AB] = s_A s_B/(d_A d_B K), with K = k_-/k₊ the dissociation constant.

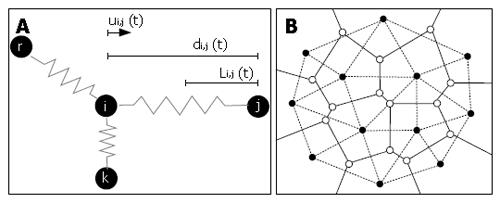
Figure 4 Schematics illustrating the lattice-free approach developed by Meineke et al[16]. (A) In silico cells attached by springs. According to Hooke’s law, the restoring force due to each spring is proportional to its net extension and acts in the opposite direction. The total force acting on a cell i is equal to the sum of all forces applied by neighbouring cells j: F_i (t) = μΣ u_i,j (t) ( d_i,j (t) - L_i,j (t) ), with μ the spring constant, L_i,j the equilibrium length of the spring between i and j, d_i,j the distance between i and j, and u_i,j the unit vector from i to j. The new position of cell i after a small time interval Δt is given by: r_i (t + Δt) = r_i (t) + F_i (t) Δt/η, with η a damping constant. (B) In silico 2D tissue, showing cell centres (black nodes) and the associated Voronoi tesselation (solid lines). The related Delauney triangulation (dashed lines) is obtained by connecting all neighbouring nodes and defines the network of springs.

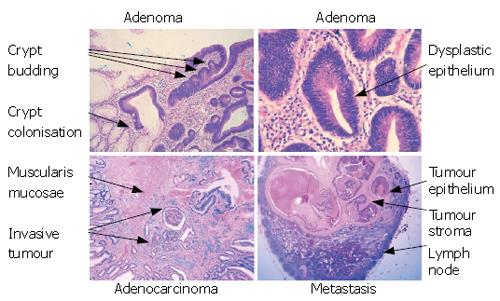
Figure 5 The stages of tumour development. Colorectal cancers develop through a variety of stages. Disruption of Wnt signalling (usually through APC mutation) will cause adenoma formation. This is manifest as dysplasia of the epithelial cells (characterised by enlargement of the epithelial nuclei, loss of mucin and deeply staining nuclei). Adenomas can grow by crypt branching and colonisation of other crypts but, importantly, remain bounded by the basement membrane. The branching of the crypts causes adenomas to develop a very complex architecture and, as more mutations accrue, the architecture becomes more complex and the cells become more severely dysplastic. Eventually the tumour cells will break through the basement membrane and invade into the stroma and this represents the transition from and adenoma into a carcinoma. Once within the stroma, the tumour cells can grow, infiltrate more deeply into the bowel wall and also can invade into lymphatic and vascular structures to allow metastasis to distant sites, such as lymph nodes. It is noteworthy that metastatic deposits also contain stroma showing the importance of the relationship between the tumour epithelium and the tumour stroma.

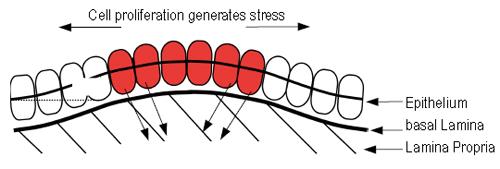
Figure 6 Schematic of the biomechanical model developed in Edwards and Chapman[44]. Proliferation in the epithelium generates stress within the layer through cellular attachment to the underlying basal lamina. For certain choices of the model parameters, the stress that is generated causes the layer to buckle, inducing a displacement y and initiating crypt budding and fission.