Towards a multiscale model of colorectal cancer

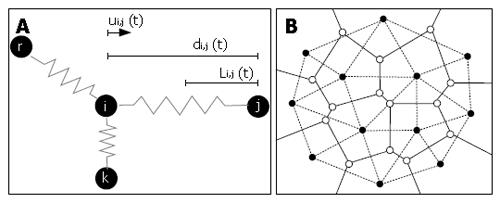
Figure 4 Schematics illustrating the lattice-free approach developed by Meineke et al[16]. (A) In silico cells attached by springs. According to Hooke’s law, the restoring force due to each spring is proportional to its net extension and acts in the opposite direction. The total force acting on a cell i is equal to the sum of all forces applied by neighbouring cells j: F_i (t) = μΣ u_i,j (t) ( d_i,j (t) - L_i,j (t) ), with μ the spring constant, L_i,j the equilibrium length of the spring between i and j, d_i,j the distance between i and j, and u_i,j the unit vector from i to j. The new position of cell i after a small time interval Δt is given by: r_i (t + Δt) = r_i (t) + F_i (t) Δt/η, with η a damping constant. (B) In silico 2D tissue, showing cell centres (black nodes) and the associated Voronoi tesselation (solid lines). The related Delauney triangulation (dashed lines) is obtained by connecting all neighbouring nodes and defines the network of springs.